随机算法 (Fall 2011)/Birthday Problem
There are [math]\displaystyle{ m }[/math] students in the class. Assume that for each student, his/her birthday is uniformly and independently distributed over the 365 days in a years. We wonder what the probability that no two students share a birthday.
Due to the pigeonhole principle, it is obvious that for [math]\displaystyle{ m\gt 365 }[/math], there must be two students with the same birthday. Surprisingly, for any [math]\displaystyle{ m\gt 57 }[/math] this event occurs with more than 99% probability. This is called the birthday paradox. Despite the name, the birthday paradox is not a real paradox.
We can model this problem as a balls-into-bins problem. [math]\displaystyle{ m }[/math] different balls (students) are uniformly and independently thrown into 365 bins (days). More generally, let [math]\displaystyle{ n }[/math] be the number of bins. We ask for the probability of the following event [math]\displaystyle{ \mathcal{E} }[/math]
- [math]\displaystyle{ \mathcal{E} }[/math]: there is no bin with more than one balls (i.e. no two students share birthday).
We first analyze this by counting. There are totally [math]\displaystyle{ n^m }[/math] ways of assigning [math]\displaystyle{ m }[/math] balls to [math]\displaystyle{ n }[/math] bins. The number of assignments that no two balls share a bin is [math]\displaystyle{ {n\choose m}m! }[/math].
Thus the probability is given by:
- [math]\displaystyle{ \begin{align} \Pr[\mathcal{E}] = \frac{{n\choose m}m!}{n^m}. \end{align} }[/math]
Recall that [math]\displaystyle{ {n\choose m}=\frac{n!}{(n-m)!m!} }[/math]. Then
- [math]\displaystyle{ \begin{align} \Pr[\mathcal{E}] = \frac{{n\choose m}m!}{n^m} = \frac{n!}{n^m(n-m)!} = \frac{n}{n}\cdot\frac{n-1}{n}\cdot\frac{n-2}{n}\cdots\frac{n-(m-1)}{n} = \prod_{k=1}^{m-1}\left(1-\frac{k}{n}\right). \end{align} }[/math]
There is also a more "probabilistic" argument for the above equation. To be rigorous, we need the following theorem, which holds generally and is very useful for computing the AND of many events.
By the definition of conditional probability, [math]\displaystyle{ \Pr[A\mid B]=\frac{\Pr[A\wedge B]}{\Pr[B]} }[/math]. Thus, [math]\displaystyle{ \Pr[A\wedge B] =\Pr[B]\cdot\Pr[A\mid B] }[/math]. This hints us that we can compute the probability of the AND of events by conditional probabilities. Formally, we have the following theorem: Theorem:
- Let [math]\displaystyle{ \mathcal{E}_1, \mathcal{E}_2, \ldots, \mathcal{E}_n }[/math] be any [math]\displaystyle{ n }[/math] events. Then
- [math]\displaystyle{ \begin{align} \Pr\left[\bigwedge_{i=1}^n\mathcal{E}_i\right] &= \prod_{k=1}^n\Pr\left[\mathcal{E}_k \mid \bigwedge_{i\lt k}\mathcal{E}_i\right]. \end{align} }[/math]
Proof: It holds that [math]\displaystyle{ \Pr[A\wedge B] =\Pr[B]\cdot\Pr[A\mid B] }[/math]. Thus, let [math]\displaystyle{ A=\mathcal{E}_n }[/math] and [math]\displaystyle{ B=\mathcal{E}_1\wedge\mathcal{E}_2\wedge\cdots\wedge\mathcal{E}_{n-1} }[/math], then
- [math]\displaystyle{ \begin{align} \Pr[\mathcal{E}_1\wedge\mathcal{E}_2\wedge\cdots\wedge\mathcal{E}_n] &= \Pr[\mathcal{E}_1\wedge\mathcal{E}_2\wedge\cdots\wedge\mathcal{E}_{n-1}]\cdot\Pr\left[\mathcal{E}_n\mid \bigwedge_{i\lt n}\mathcal{E}_i\right]. \end{align} }[/math]
Recursively applying this equation to [math]\displaystyle{ \Pr[\mathcal{E}_1\wedge\mathcal{E}_2\wedge\cdots\wedge\mathcal{E}_{n-1}] }[/math] until there is only [math]\displaystyle{ \mathcal{E}_1 }[/math] left, the theorem is proved. [math]\displaystyle{ \square }[/math]
- Let [math]\displaystyle{ \mathcal{E}_1, \mathcal{E}_2, \ldots, \mathcal{E}_n }[/math] be any [math]\displaystyle{ n }[/math] events. Then
Now we are back to the probabilistic analysis of the birthday problem, with a general setting of [math]\displaystyle{ m }[/math] students and [math]\displaystyle{ n }[/math] possible birthdays (imagine that we live in a planet where a year has [math]\displaystyle{ n }[/math] days).
The first student has a birthday (of course!). The probability that the second student has a different birthday is [math]\displaystyle{ \left(1-\frac{1}{n}\right) }[/math]. Given that the first two students have different birthdays, the probability that the third student has a different birthday from the first two is [math]\displaystyle{ \left(1-\frac{2}{n}\right) }[/math]. Continuing this on, assuming that the first [math]\displaystyle{ k-1 }[/math] students all have different birthdays, the probability that the [math]\displaystyle{ k }[/math]th student has a different birthday than the first [math]\displaystyle{ k-1 }[/math], is given by [math]\displaystyle{ \left(1-\frac{k-1}{n}\right) }[/math]. So the probability that all [math]\displaystyle{ m }[/math] students have different birthdays is the product of all these conditional probabilities:
- [math]\displaystyle{ \begin{align} \Pr[\mathcal{E}]=\left(1-\frac{1}{n}\right)\cdot \left(1-\frac{2}{n}\right)\cdots \left(1-\frac{m-1}{n}\right) &= \prod_{k=1}^{m-1}\left(1-\frac{k}{n}\right), \end{align} }[/math]
which is the same as what we got by the counting argument.
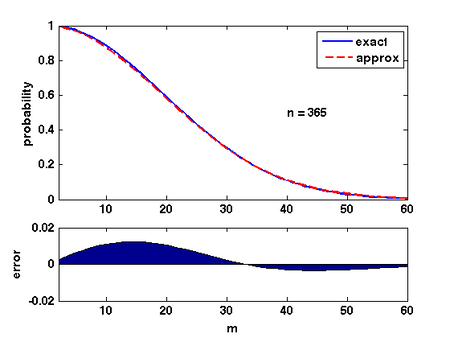
There are several ways of analyzing this formular. Here is a convenient one: Due to Taylor's expansion, [math]\displaystyle{ e^{-k/n}\approx 1-k/n }[/math]. Then
- [math]\displaystyle{ \begin{align} \prod_{k=1}^{m-1}\left(1-\frac{k}{n}\right) &\approx \prod_{k=1}^{m-1}e^{-\frac{k}{n}}\\ &= \exp\left(-\sum_{k=1}^{m-1}\frac{k}{n}\right)\\ &= e^{-m(m-1)/2n}\\ &\approx e^{-m^2/2n}. \end{align} }[/math]
The quality of this approximation is shown in the Figure.
Therefore, for [math]\displaystyle{ m=\sqrt{2n\ln \frac{1}{\epsilon}} }[/math], the probability that [math]\displaystyle{ \Pr[\mathcal{E}]\approx\epsilon }[/math].