随机算法 (Fall 2011)/Coupling
Coupling of Two Distributions
Coupling is a powerful proof technique in probability theory. It allows us to compare two unrelated variables (or processes) by forcing them to share some randomness.
Definition (coupling) - Let [math]\displaystyle{ p }[/math] and [math]\displaystyle{ q }[/math] be two probability distributions over [math]\displaystyle{ \Omega }[/math]. A probability distribution [math]\displaystyle{ \mu }[/math] over [math]\displaystyle{ \Omega\times\Omega }[/math] is said to be a coupling if its marginal distributions are [math]\displaystyle{ p }[/math] and [math]\displaystyle{ q }[/math]; that is
- [math]\displaystyle{ \begin{align} p(x) &=\sum_{y\in\Omega}\mu(x,y);\\ q(x) &=\sum_{y\in\Omega}\mu(y,x). \end{align} }[/math]
- Let [math]\displaystyle{ p }[/math] and [math]\displaystyle{ q }[/math] be two probability distributions over [math]\displaystyle{ \Omega }[/math]. A probability distribution [math]\displaystyle{ \mu }[/math] over [math]\displaystyle{ \Omega\times\Omega }[/math] is said to be a coupling if its marginal distributions are [math]\displaystyle{ p }[/math] and [math]\displaystyle{ q }[/math]; that is
The interesting case is when [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] are not independent. In particular, we want the probability that [math]\displaystyle{ X=Y }[/math] to be as large as possible, yet still maintaining the respective marginal distributions [math]\displaystyle{ p }[/math] and [math]\displaystyle{ q }[/math]. When [math]\displaystyle{ p }[/math] and [math]\displaystyle{ q }[/math] are different it is inevitable that [math]\displaystyle{ X\neq Y }[/math] with some probability, but how small this probability can be, that is, how well two distributions can be coupled? The following coupling lemma states that this is determined by the total variation distance between the two distributions.
Lemma (coupling lemma) - Let [math]\displaystyle{ p }[/math] and [math]\displaystyle{ q }[/math] be two probability distributions over [math]\displaystyle{ \Omega }[/math].
- For any coupling [math]\displaystyle{ (X,Y) }[/math] of [math]\displaystyle{ p }[/math] and [math]\displaystyle{ q }[/math], it holds that [math]\displaystyle{ \Pr[X\neq Y]\ge\|p-q\|_{TV} }[/math].
- There exists a coupling [math]\displaystyle{ (X,Y) }[/math] of [math]\displaystyle{ p }[/math] and [math]\displaystyle{ q }[/math] such that [math]\displaystyle{ \Pr[X\neq Y]=\|p-q\|_{TV} }[/math].
Proof. - 1.
Suppose [math]\displaystyle{ (X,Y) }[/math] follows the distribution [math]\displaystyle{ \mu }[/math] over [math]\displaystyle{ \Omega\times\Omega }[/math]. Due to the definition of coupling,
- [math]\displaystyle{ \begin{align} p(x) =\sum_{y\in\Omega}\mu(x,y) &\quad\text{and } &q(x) =\sum_{y\in\Omega}\mu(y,x). \end{align} }[/math]
Then for any [math]\displaystyle{ z\in\Omega }[/math], [math]\displaystyle{ \mu(z,z)\le\min\{p(z),q(z)\} }[/math], thus
- [math]\displaystyle{ \begin{align} \Pr[X=Y] &= \sum_{z\in\Omega}\mu(z,z) \le\sum_{z\in\Omega}\min\{p(z),q(z)\}. \end{align} }[/math]
Therefore,
- [math]\displaystyle{ \begin{align} \Pr[X\neq Y] &\ge 1-\sum_{z\in\Omega}\min\{p(z),q(z)\}\\ &=\sum_{z\in\Omega}(p(z)-\min\{p(z),q(z)\})\\ &=\sum_{z\in\Omega\atop p(z)\gt q(z)}(p(z)-q(z))\\ &=\frac{1}{2}\sum_{z\in\Omega}|p(z)-q(z)|\\ &=\|p-q\|_{TV}. \end{align} }[/math]
- 2.
We can couple [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] so that for each [math]\displaystyle{ z\in\Omega }[/math], [math]\displaystyle{ X=Y=z }[/math] with probability [math]\displaystyle{ \min\{p(z),q(z)\} }[/math]. The remaining follows as above.
- [math]\displaystyle{ \square }[/math]
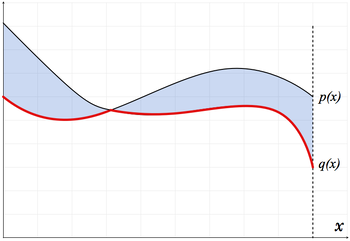
The proof is depicted by the following figure, where the curves are the probability density functions for the two distributions [math]\displaystyle{ p }[/math] and [math]\displaystyle{ q }[/math], the colored area is the diference between the two distribution, and the "lower envelope" (the red line) is the [math]\displaystyle{ \min\{p(x), q(x)\} }[/math].
Monotonicity of [math]\displaystyle{ \Delta_x(t) }[/math]
Consider a Markov chain on state space [math]\displaystyle{ \Omega }[/math]. Let [math]\displaystyle{ \pi }[/math] be the stationary distribution, and [math]\displaystyle{ p_x^{(t)} }[/math] be the distribution after [math]\displaystyle{ t }[/math] steps when the initial state is [math]\displaystyle{ x }[/math]. Recall that [math]\displaystyle{ \Delta_x(t)=\|p_x^{(t)}-\pi\|_{TV} }[/math] is the distance to stationary distribution [math]\displaystyle{ \pi }[/math] after [math]\displaystyle{ t }[/math] steps, started at state [math]\displaystyle{ x }[/math].
We will show that [math]\displaystyle{ \Delta_x(t) }[/math] is non-decreasing in [math]\displaystyle{ t }[/math]. That is, for a Markov chain, the variation distance to the stationary distribution monotonically decreases as time passes. Although this is rather intuitive at the first glance, the proof is nontrivial. A brute force (algebraic) proof can be obtained by analyze the change to the 1-norm of [math]\displaystyle{ p_x^{(t)}-\pi }[/math] by multiplying the transition matrix [math]\displaystyle{ P }[/math]. The analysis uses eigen decomposition. We introduce a cleverer proof using coupling.
Proposition - [math]\displaystyle{ \Delta_x(t) }[/math] is non-decreasing in [math]\displaystyle{ t }[/math].
Proof. Let [math]\displaystyle{ X_0=x }[/math] and [math]\displaystyle{ Y_0 }[/math] follow the stationary distribution [math]\displaystyle{ \pi }[/math]. Two chains [math]\displaystyle{ X_0,X_1,X_2,\ldots }[/math] and [math]\displaystyle{ Y_0,Y_1,Y_2,\ldots }[/math] can be defined by the initial distributions [math]\displaystyle{ X_0 }[/math] and [math]\displaystyle{ Y_0 }[/math]. The distributions of [math]\displaystyle{ X_t }[/math] and [math]\displaystyle{ Y_t }[/math] are [math]\displaystyle{ p_x^{(t)} }[/math] and [math]\displaystyle{ \pi }[/math], respectively.
For any fixed [math]\displaystyle{ t }[/math], we can couple [math]\displaystyle{ X_t }[/math] and [math]\displaystyle{ Y_t }[/math] such that [math]\displaystyle{ \Pr[X\neq Y]=\|p_x^{t}-\pi\|_{TV}=\Delta_x(t) }[/math]. Due to the Coupling Lemma, such coupling exists. We then define a coupling between [math]\displaystyle{ X_{t+1} }[/math] and [math]\displaystyle{ Y_{t+1} }[/math] as follows.
- If [math]\displaystyle{ X_t=Y_t }[/math], then [math]\displaystyle{ X_{t+1}=Y_{t+1} }[/math] following the transition matrix of the Markov chain.
- Otherwise, do the transitions [math]\displaystyle{ X_t\rightarrow X_{t+1} }[/math] and [math]\displaystyle{ Y_t\rightarrow Y_{t+1} }[/math] independently, following the transitin matrix.
It is easy to see that the marginal distributions of [math]\displaystyle{ X_{t+1} }[/math] and [math]\displaystyle{ Y_{t+1} }[/math] both follow the original Markov chain, and
- [math]\displaystyle{ \Pr[X_{t+1}\neq Y_{t+1}]\le \Pr[X_t\neq Y_{t}]. }[/math]
In conclusion, it holds that
- [math]\displaystyle{ \Delta_x(t+1)=\|p_x^{(t+1)}-\pi\|_{TV}\le\Pr[X_{t+1}\neq Y_{t+1}]\le \Pr[X_t\neq Y_{t}]=\Delta_x(t), }[/math]
where the first inequality is due to the easy direction of the Coupling Lemma.
- [math]\displaystyle{ \square }[/math]
Rapid Mixing by Coupling
Consider an ergodic (irreducible and aperiodic) Markov chain on state space [math]\displaystyle{ \Omega }[/math]. We want to upper bound its mixing time. The coupling technique for bounding the mixing time can be sumerized as follows:
- Consider two random walks starting at state [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] in [math]\displaystyle{ \Omega }[/math]. Each individual walk follows the transition rule of the original Markov chain. But the two random walks may be "coupled" in some way, that is, may be correlated with each other. A key observation is that for any such coupling, it always holds that
- [math]\displaystyle{ \Delta(t) \le\max_{x,y\in\Omega}\Pr[\text{ the two } \mathit{coupled} \text{ random walks started at }x,y\text{ have not met by time }t] }[/math]
- where we recall that [math]\displaystyle{ \Delta(t)=\max_{x\in\Omega}\|p_x^{(t)}-\pi\|_{TV} }[/math].
Definition (coupling of Markov chain) - A coupling of a Markov chain with state space [math]\displaystyle{ \Omega }[/math] and transition matrix [math]\displaystyle{ P }[/math], is a Markov chain [math]\displaystyle{ (X_t,Y_t) }[/math] with state space [math]\displaystyle{ \Omega\times\Omega }[/math], satisfying
- each of [math]\displaystyle{ X_t }[/math] and [math]\displaystyle{ Y_t }[/math] viewed in isolation is a faithful copy of the original Markov chain, i.e.
- [math]\displaystyle{ \Pr[X_{t+1}=v\mid X_t=u]=\Pr[Y_{t+1}=v\mid Y_{t}=u]=P(u,v) }[/math];
- once [math]\displaystyle{ X_t }[/math] and [math]\displaystyle{ Y_t }[/math] reaches the same state, they make identical moves ever since, i.e.
- [math]\displaystyle{ X_{t+1}=Y_{t+1} }[/math] if [math]\displaystyle{ X_t=Y_t }[/math].
Lemma (coupling lemma for Markov chains) - Let [math]\displaystyle{ (X_t,Y_t) }[/math] be a coupling of a Markov chain [math]\displaystyle{ M }[/math] with state space [math]\displaystyle{ \Omega }[/math]. Then [math]\displaystyle{ \Delta(t) }[/math] for [math]\displaystyle{ M }[/math] is bounded by
- [math]\displaystyle{ \Delta(t) \le\max_{x,y\in\Omega}\Pr[X_t\neq Y_t\mid X_0=x,Y_0=y] }[/math].
- Let [math]\displaystyle{ (X_t,Y_t) }[/math] be a coupling of a Markov chain [math]\displaystyle{ M }[/math] with state space [math]\displaystyle{ \Omega }[/math]. Then [math]\displaystyle{ \Delta(t) }[/math] for [math]\displaystyle{ M }[/math] is bounded by
Proof. Due to the coupling lemma (for probability distributions),
- [math]\displaystyle{ \Pr[X_t\neq Y_t\mid X_0=x,Y_0=y] \ge \|p_x^{(t)}-p_y^{(t)}\|_{TV}, }[/math]
where [math]\displaystyle{ p_x^{(t)},p_y^{(t)} }[/math] are distributions of the Markov chain [math]\displaystyle{ M }[/math] at time [math]\displaystyle{ t }[/math], started at states [math]\displaystyle{ x, y }[/math].
Therefore,
- [math]\displaystyle{ \begin{align} \Delta(t) &= \max_{x\in\Omega}\|p_x^{(t)}-\pi\|_{TV}\\ &\le \max_{x,y\in\Omega}\|p_x^{(t)}-p_y^{(t)}\|_{TV}\\ &\le \max_{x,y\in\Omega}\Pr[X_t\neq Y_t\mid X_0=x,Y_0=y]. \end{align} }[/math]
- [math]\displaystyle{ \square }[/math]
Corollary - Let [math]\displaystyle{ (X_t,Y_t) }[/math] be a coupling of a Markov chain [math]\displaystyle{ M }[/math] with state space [math]\displaystyle{ \Omega }[/math]. Then [math]\displaystyle{ \tau(\epsilon) }[/math] for [math]\displaystyle{ M }[/math] is bounded as follows:
- [math]\displaystyle{ \max_{x,y\in\Omega}\Pr[X_t\neq Y_t\mid X_0=x,Y_0=y]\le \epsilon\quad\Longrightarrow\quad\tau(\epsilon)\le t }[/math].
- Let [math]\displaystyle{ (X_t,Y_t) }[/math] be a coupling of a Markov chain [math]\displaystyle{ M }[/math] with state space [math]\displaystyle{ \Omega }[/math]. Then [math]\displaystyle{ \tau(\epsilon) }[/math] for [math]\displaystyle{ M }[/math] is bounded as follows:
Geometric convergence
Consider a Markov chain on state space [math]\displaystyle{ \Omega }[/math]. Let [math]\displaystyle{ \pi }[/math] be the stationary distribution, and [math]\displaystyle{ p_x^{(t)} }[/math] be the distribution after [math]\displaystyle{ t }[/math] steps when the initial state is [math]\displaystyle{ x }[/math]. Recall that
- [math]\displaystyle{ \Delta_x(t)=\|p_x^{(t)}-\pi\|_{TV} }[/math];
- [math]\displaystyle{ \Delta(t)=\max_{x\in\Omega}\Delta_x(t) }[/math];
- [math]\displaystyle{ \tau_x(\epsilon)=\min\{t\mid\Delta_x(t)\le\epsilon\} }[/math];
- [math]\displaystyle{ \tau(\epsilon)=\max_{x\in\Omega}\tau_x(\epsilon) }[/math];
- [math]\displaystyle{ \tau_{\mathrm{mix}}=\tau(1/2\mathrm{e})\, }[/math].
We prove that
Proposition - [math]\displaystyle{ \Delta(k\cdot\tau_{\mathrm{mix}})\le \mathrm{e}^{-k} }[/math] for any integer [math]\displaystyle{ k\ge1 }[/math].
- [math]\displaystyle{ \tau(\epsilon)\le\tau_{\mathrm{mix}}\cdot\left\lceil\ln\frac{1}{\epsilon}\right\rceil }[/math].
Proof. - 1.
We denote that [math]\displaystyle{ \tau=\tau_{\mathrm{mix}}\, }[/math]. We construct a coupling of the Markov chain as follows. Suppose [math]\displaystyle{ t=k\tau }[/math] for some integer [math]\displaystyle{ k }[/math].
- If [math]\displaystyle{ X_t=Y_t }[/math] then [math]\displaystyle{ X_{t+i}=Y_{t+i} }[/math] for [math]\displaystyle{ i=1,2,\ldots,\tau }[/math].
- For the case that [math]\displaystyle{ X_t=u, Y_t=v }[/math] for some [math]\displaystyle{ u\neq v }[/math], we couple the [math]\displaystyle{ X_{t+\tau} }[/math] and [math]\displaystyle{ Y_{t+\tau} }[/math] so that [math]\displaystyle{ \Pr[X_{t+\tau}\neq Y_{t+\tau}\mid X_t=u,Y_t=v]=\|p_u^{(t)}-p_v^{(t)}\|_{TV} }[/math]. Due to the Coupling Lemma, such coupling does exist.
For any [math]\displaystyle{ u,v\in\Omega }[/math] that [math]\displaystyle{ u\neq v }[/math],
- [math]\displaystyle{ \begin{align} \Pr[X_{t+\tau}\neq Y_{t+\tau}\mid X_t=u,Y_t=v] &=\|p_u^{(t)}-p_v^{(t)}\|_{TV}\\ &\le \|p_u^{(\tau)}-\pi\|_{TV}+\|p_v^{(\tau)}-\pi\|_{TV}\\ &= \Delta_u(\tau)+\Delta_v(\tau)\\ &\le \frac{1}{\mathrm{e}}. \end{align} }[/math]
Thus [math]\displaystyle{ \Pr[X_{t+\tau}\neq Y_{t+\tau}\mid X_t\neq Y_t]\le \frac{1}{\mathrm{e}} }[/math] by the law of total probability. Therefore, for any [math]\displaystyle{ x,y\in\Omega }[/math],
- [math]\displaystyle{ \begin{align} &\quad\, \Pr[X_{t+\tau}\neq Y_{t+\tau}\mid X_0=x,Y_0=y]\\ &= \Pr[X_{t+\tau}\neq Y_{t+\tau}\mid X_t\neq Y_t]\cdot \Pr[X_{t}\neq Y_{t}\mid X_0=x,Y_0=y]\\ &\le \frac{1}{\mathrm{e}}\Pr[X_{t}\neq Y_{t}\mid X_0=x,Y_0=y]. \end{align} }[/math]
Then by induction,
- [math]\displaystyle{ \Pr[X_{k\tau}\neq Y_{k\tau}\mid X_0=x,Y_0=y]\le \mathrm{e}^{-k}, }[/math]
and this holds for any [math]\displaystyle{ x,y\in\Omega }[/math]. By the Coupling Lemma for Markov chains, this means [math]\displaystyle{ \Delta(k\tau_{\mathrm{mix}})=\Delta(k\tau)\le\mathrm{e}^{-k} }[/math].
- 2.
By the definition of [math]\displaystyle{ \tau(\epsilon) }[/math], the inequality is straightforwardly implied by (1).
- [math]\displaystyle{ \square }[/math]
Random Walk on the Hypercube
A [math]\displaystyle{ n }[/math]-dimensional hypercube is a graph on vertex set [math]\displaystyle{ \{0,1\}^n }[/math]. For any [math]\displaystyle{ x,y\in\{0,1\}^n }[/math], there is an edge between [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] if [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] differ at exact one coordinate (the hamming distance between [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] is 1).
We use coupling to bound the mixing time of the following simple random walk on a hypercube.
Random Walk on Hypercube - At each step, for the current state [math]\displaystyle{ x\in\{0,1\}^n }[/math]:
- with probability [math]\displaystyle{ 1/2 }[/math], do nothing;
- else, pick a coordinate [math]\displaystyle{ i\in\{1,2,\ldots,n\} }[/math] uniformly at random and flip the bit [math]\displaystyle{ x_i }[/math] (change [math]\displaystyle{ x_i }[/math] to [math]\displaystyle{ 1-x_i }[/math]).
This is a lazy uniform random walk in an [math]\displaystyle{ n }[/math]-dimensional hypercube. It is equivalent to the following random walk.
Random Walk on Hypercube - At each step, for the current state [math]\displaystyle{ x\in\{0,1\}^n }[/math]:
- pick a coordinate [math]\displaystyle{ i\in\{1,2,\ldots,n\} }[/math] uniformly at random and a bit [math]\displaystyle{ b\in\{0,1\} }[/math] uniformly at random;
- let [math]\displaystyle{ x_i=b }[/math].
It is easy to see the two random walks are the same. The second form hint us to couple the random choice of [math]\displaystyle{ i }[/math] and [math]\displaystyle{ b }[/math] in each step. Consider two copies of the random walk [math]\displaystyle{ X_t }[/math] and [math]\displaystyle{ Y_t }[/math], started from arbitrary two states [math]\displaystyle{ X_0 }[/math] and [math]\displaystyle{ Y_0 }[/math], the coupling rule is:
- At each step, [math]\displaystyle{ X_t }[/math] and [math]\displaystyle{ Y_t }[/math] choose the same (uniformly random) coordinate [math]\displaystyle{ i }[/math] and the same (uniformly random) bit [math]\displaystyle{ b }[/math].
Obviously the two individual random walks are both faithful copies of the original walk.
For arbitrary [math]\displaystyle{ x,y\in\{0,1\}^n }[/math], started at [math]\displaystyle{ X_0=x, Y_0=y }[/math], the event [math]\displaystyle{ X_t=Y_t }[/math] occurs if everyone of the coordinates on which [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] disagree has been picked at least once. In the worst case, [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] disagree on all [math]\displaystyle{ n }[/math] coordinates. The time [math]\displaystyle{ T }[/math] that all [math]\displaystyle{ n }[/math] coordinates have been picked follows the coupon collector problem collecting [math]\displaystyle{ n }[/math] coupons, and we know from the coupon collector problem that for [math]\displaystyle{ c\gt 0 }[/math],
- [math]\displaystyle{ \Pr[T\ge n\ln n+cn]\le \mathrm{e}^{-c}. }[/math]
Thus for any [math]\displaystyle{ x,y\in\{0,1\}^n }[/math], if [math]\displaystyle{ t\ge n\ln n+cn }[/math], then [math]\displaystyle{ \Pr[X_t\neq Y_t\mid X_0=x,Y_0=y]\le \mathrm{e}^{-c} }[/math]. Due to the coupling lemma for Markov chains,
- [math]\displaystyle{ \Delta(n\ln n+cn)\le \mathrm{e}^{-c}, }[/math]
which implies that
- [math]\displaystyle{ \tau(\epsilon)=n\ln n+n\ln\frac{1}{\epsilon} }[/math].
So the random walk achieves a polynomially small variation distance [math]\displaystyle{ \epsilon=\frac{1}{\mathrm{poly}(n)} }[/math] to the stationary distribution in time [math]\displaystyle{ O(n\ln n) }[/math].
Note that the number of states (vertices in the [math]\displaystyle{ n }[/math]-dimensional hypercube) is [math]\displaystyle{ 2^n }[/math]. Therefore, the mixing time is exponentially small compared to the size of the state space.