随机算法 (Fall 2011)/Perfect hashing
Collision number
Consider a 2-universal family [math]\displaystyle{ \mathcal{H} }[/math] of hash functions from [math]\displaystyle{ [N] }[/math] to [math]\displaystyle{ [M] }[/math]. Let [math]\displaystyle{ h }[/math] be a hash function chosen uniformly from [math]\displaystyle{ \mathcal{H} }[/math]. For a fixed set [math]\displaystyle{ S }[/math] of [math]\displaystyle{ n }[/math] distinct elements from [math]\displaystyle{ [N] }[/math], say [math]\displaystyle{ S=\{x_1,x_2,\ldots,x_n\} }[/math], the elements are mapped to the hash values [math]\displaystyle{ h(x_1), h(x_2), \ldots, h(x_n) }[/math]. This can be seen as throwing [math]\displaystyle{ n }[/math] balls to [math]\displaystyle{ M }[/math] bins, with pairwise independent choices of bins.
As in the balls-into-bins with full independence, we are curious about the questions such as the birthday problem or the maximum load. These questions are interesting not only because they are natural to ask in a balls-into-bins setting, but in the context of hashing, they are closely related to the performance of hash functions.
The old techniques for analyzing balls-into-bins rely too much on the independence of the choice of the bin for each ball, therefore can hardly be extended to the setting of 2-universal hash families. However, it turns out several balls-into-bins questions can somehow be answered by analyzing a very natural quantity: the number of collision pairs.
A collision pair for hashing is a pair of elements [math]\displaystyle{ x_1,x_2\in S }[/math] which are mapped to the same hash value, i.e. [math]\displaystyle{ h(x_1)=h(x_2) }[/math]. Formally, for a fixed set of elements [math]\displaystyle{ S=\{x_1,x_2,\ldots,x_n\} }[/math], for any [math]\displaystyle{ 1\le i,j\le n }[/math], let the random variable
- [math]\displaystyle{ X_{ij} = \begin{cases} 1 & \text{if }h(x_i)=h(x_j),\\ 0 & \text{otherwise.} \end{cases} }[/math]
The total number of collision pairs among the [math]\displaystyle{ n }[/math] items [math]\displaystyle{ x_1,x_2,\ldots,x_n }[/math] is
- [math]\displaystyle{ X=\sum_{i\lt j} X_{ij}.\, }[/math]
Since [math]\displaystyle{ \mathcal{H} }[/math] is 2-universal, for any [math]\displaystyle{ i\neq j }[/math],
- [math]\displaystyle{ \Pr[X_{ij}=1]=\Pr[h(x_i)=h(x_j)]\le\frac{1}{M}. }[/math]
The expected number of collision pairs is
- [math]\displaystyle{ \mathbf{E}[X]=\mathbf{E}\left[\sum_{i\lt j}X_{ij}\right]=\sum_{i\lt j}\mathbf{E}[X_{ij}]=\sum_{i\lt j}\Pr[X_{ij}=1]\le{n\choose 2}\frac{1}{M}\lt \frac{n^2}{2M}. }[/math]
In particular, for [math]\displaystyle{ n=M }[/math], i.e. [math]\displaystyle{ n }[/math] items are mapped to [math]\displaystyle{ n }[/math] hash values by a pairwise independent hash function, the expected collision number is [math]\displaystyle{ \mathbf{E}[X]\lt \frac{n^2}{2M}=\frac{n}{2} }[/math].
Perfect hashing
Perfect hashing is a data structure for storing a static dictionary. In a static dictionary, a set [math]\displaystyle{ S }[/math] of [math]\displaystyle{ n }[/math] items from the universe [math]\displaystyle{ [N] }[/math] are preprocessed and stored in a table. Once the table is constructed, it will nit be changed any more, but will only be used for search operations: a search for an item gives the location of the item in the table or returns that the item is not in the table. You may think of an application that we store an encyclopedia in a DVD, so that searches are very efficient but there will be no updates to the data.
This problem can be solved by binary search on a sorted table or balanced search trees in [math]\displaystyle{ O(\log n) }[/math] time for a set [math]\displaystyle{ S }[/math] of [math]\displaystyle{ n }[/math] elements. We show how to solve this problem with [math]\displaystyle{ O(1) }[/math] time by perfect hashing.
The idea of perfect hashing is that we use a hash function [math]\displaystyle{ h }[/math] to map the [math]\displaystyle{ n }[/math] items to distinct entries of the table; store every item [math]\displaystyle{ x\in S }[/math] in the entry [math]\displaystyle{ h(x) }[/math]; and also store the hash function [math]\displaystyle{ h }[/math] in a fixed location in the table (usually the beginning of the table). The algorithm for searching for an item is as follows:
- search for [math]\displaystyle{ x }[/math] in table [math]\displaystyle{ T }[/math]:
- retrieve [math]\displaystyle{ h }[/math] from a fixed location in the table;
- if [math]\displaystyle{ x=T[h(x)] }[/math] return [math]\displaystyle{ h(x) }[/math]; else return NOT_FOUND;
This scheme works as long as that the hash function satisfies the following two conditions:
- The description of [math]\displaystyle{ h }[/math] is sufficiently short, so that [math]\displaystyle{ h }[/math] can be stored in one entry (or in constant many entries) of the table.
- [math]\displaystyle{ h }[/math] has no collisions on [math]\displaystyle{ S }[/math], i.e. there is no pair of items [math]\displaystyle{ x_1,x_2\in S }[/math] that are mapped to the same value by [math]\displaystyle{ h }[/math].
The first condition is easy to guarantee for 2-universal hash families. As shown by Carter-Wegman construction, a 2-universal hash function can be uniquely represented by two integers [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math], which can be stored in two entries (or just one, if the word length is sufficiently large) of the table.
Our discussion is now focused on the second condition. We find that it relies on the perfectness of the hash function for a data set [math]\displaystyle{ S }[/math].
A hash function [math]\displaystyle{ h }[/math] is perfect for a set [math]\displaystyle{ S }[/math] of items if [math]\displaystyle{ h }[/math] maps all items in [math]\displaystyle{ S }[/math] to different values, i.e. there is no collision.
We have shown by the birthday problem for 2-universal hashing that when [math]\displaystyle{ n }[/math] items are mapped to [math]\displaystyle{ n^2 }[/math] values, for an [math]\displaystyle{ h }[/math] chosen uniformly from a 2-universal family of hash functions, the probability that a collision occurs is at most 1/2. Thus
- [math]\displaystyle{ \Pr[h\mbox{ is perfect for }S]\ge\frac{1}{2} }[/math]
for a table of [math]\displaystyle{ n^2 }[/math] entries.
The construction of perfect hashing is straightforward then:
- For a set [math]\displaystyle{ S }[/math] of [math]\displaystyle{ n }[/math] elements:
- uniformly choose an [math]\displaystyle{ h }[/math] from a 2-universal family [math]\displaystyle{ \mathcal{H} }[/math]; (for Carter-Wegman's construction, it means uniformly choose two integer [math]\displaystyle{ 1\le a\le p-1 }[/math] and [math]\displaystyle{ b\in[p] }[/math] for a sufficiently large prime [math]\displaystyle{ p }[/math].)
- check whether [math]\displaystyle{ h }[/math] is perfect for [math]\displaystyle{ S }[/math];
- if [math]\displaystyle{ h }[/math] is NOT perfect for [math]\displaystyle{ S }[/math], start over again; otherwise, construct the table;
This is a Las Vegas randomized algorithm, which construct a perfect hashing for a fixed set [math]\displaystyle{ S }[/math] with expectedly at most two trials (due to geometric distribution). The resulting data structure is a [math]\displaystyle{ O(n^2) }[/math]-size static dictionary of [math]\displaystyle{ n }[/math] elements which answers every search in deterministic [math]\displaystyle{ O(1) }[/math] time.
FKS perfect hashing
In the last section we see how to use [math]\displaystyle{ O(n^2) }[/math] space and constant time for answering search in a set. Now we see how to do it with linear space and constant time. This solves the problem of searching asymptotically optimal for both time and space.
This was once seemingly impossible, until Yao's seminal paper:
- Yao. Should tables be sorted? Journal of the ACM (JACM), 1981.
Yao's paper shows a possibility of achieving linear space and constant time at the same time by exploiting the power of hashing, but assumes an unrealistically large universe.
Inspired by Yao's work, Fredman, Komlós, and Szemerédi discover the first linear-space and constant-time static dictionary in a realistic setting:
- Fredman, Komlós, and Szemerédi. Storing a sparse table with O(1) worst case access time. Journal of the ACM (JACM), 1984.
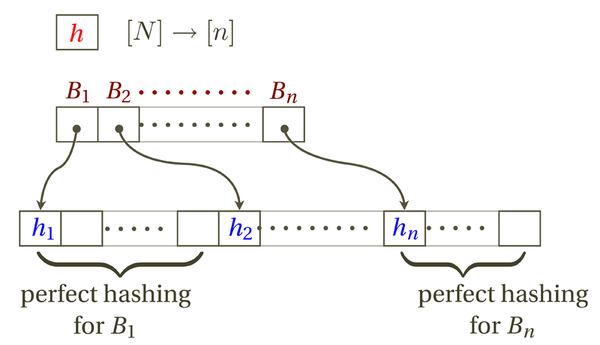
The idea of FKS hashing is to arrange hash table in two levels:
- In the first level, [math]\displaystyle{ n }[/math] items are hashed to [math]\displaystyle{ n }[/math] buckets by a 2-universal hash function [math]\displaystyle{ h }[/math].
- Let [math]\displaystyle{ B_i }[/math] be the set of items hashed to the [math]\displaystyle{ i }[/math]th bucket.
- In the second level, construct a [math]\displaystyle{ |B_i|^2 }[/math]-size perfect hashing for each bucket [math]\displaystyle{ B_i }[/math].
The data structure can be stored in a table. The first few entries are reserved to store the primary hash function [math]\displaystyle{ h }[/math]. To help the searching algorithm locate a bucket, we use the next [math]\displaystyle{ n }[/math] entries of the table as the "pointers" to the bucket: each entry stores the address of the first entry of the space to store a bucket. In the rest of table, the [math]\displaystyle{ n }[/math] buckets are stored in order, each using a [math]\displaystyle{ |B_i|^2 }[/math] space as required by perfect hashing.
It is easy to see that the search time is constant. To search for an item [math]\displaystyle{ x }[/math], the algorithm does the followings:
- Retrieve [math]\displaystyle{ h }[/math].
- Retrieve the address for bucket [math]\displaystyle{ h(x) }[/math].
- Search by perfect hashing within bucket [math]\displaystyle{ h(x) }[/math].
Each line takes constant time. So the worst-case search time is constant.
We then need to guarantee that the space is linear to [math]\displaystyle{ n }[/math]. At the first glance, this seems impossible because each instance of perfect hashing for a bucket costs a square-size of space. We will prove that although the individual buckets use square-sized spaces, the sum of the them is still linear.
For a fixed set [math]\displaystyle{ S }[/math] of [math]\displaystyle{ n }[/math] items, for a hash function [math]\displaystyle{ h }[/math] chosen uniformly from a 2-universe family which maps the items to [math]\displaystyle{ [n] }[/math], called [math]\displaystyle{ n }[/math] buckets, let [math]\displaystyle{ Y_i=|B_i| }[/math] be the number of items in [math]\displaystyle{ S }[/math] mapped to the [math]\displaystyle{ i }[/math]th bucket. We are going to bound the following quantity:
- [math]\displaystyle{ Y=\sum_{i=1}^n Y_i^2. }[/math]
Since each bucket [math]\displaystyle{ B_i }[/math] use a space of [math]\displaystyle{ Y_i^2 }[/math] for perfect hashing. [math]\displaystyle{ Y }[/math] gives the size of the space for storing the buckets.
We will show that [math]\displaystyle{ Y }[/math] is related to the total number of collision pairs. (Indeed, the number of collision pairs can be computed by a degree-2 polynomial, just like [math]\displaystyle{ Y }[/math].)
Note that a bucket of [math]\displaystyle{ Y_i }[/math] items contributes [math]\displaystyle{ {Y_i\choose 2} }[/math] collision pairs. Let [math]\displaystyle{ X }[/math] be the total number of collision pairs. [math]\displaystyle{ X }[/math] can be computed by summing over the collision pairs in every bucket:
- [math]\displaystyle{ X=\sum_{i=1}^n{Y_i\choose 2}=\sum_{i=1}^n\frac{Y_i(Y_i-1)}{2}=\frac{1}{2}\left(\sum_{i=1}^nY_i^2-\sum_{i=1}^nY_i\right)=\frac{1}{2}\left(\sum_{i=1}^nY_i^2-n\right). }[/math]
Therefore, the sum of squares of the sizes of buckets is related to collision number by:
- [math]\displaystyle{ \sum_{i=1}^nY_i^2=2X+n. }[/math]
By our analysis of the collision number, we know that for [math]\displaystyle{ n }[/math] items mapped to [math]\displaystyle{ n }[/math] buckets, the expected number of collision pairs is: [math]\displaystyle{ \mathbf{E}[X]\le \frac{n}{2} }[/math]. Thus,
- [math]\displaystyle{ \mathbf{E}\left[\sum_{i=1}^nY_i^2\right]=\mathbf{E}[2X+n]\le 2n. }[/math]
Due to Markov's inequality, [math]\displaystyle{ \sum_{i=1}^nY_i^2=O(n) }[/math] with a constant probability. For any set [math]\displaystyle{ S }[/math], we can find a suitable [math]\displaystyle{ h }[/math] after expected constant number of trials, and FKS can be constructed with guaranteed (instead of expected) linear-size which answers each search in constant time.