随机算法 (Fall 2015)/Identity Testing
Checking Matrix Multiplication
Let [math]\displaystyle{ \mathbb{F} }[/math] be a feild (you may think of it as the filed [math]\displaystyle{ \mathbb{Q} }[/math] of rational numbers, or the finite field [math]\displaystyle{ \mathbb{Z}_p }[/math] of integers modulo prime [math]\displaystyle{ p }[/math]). We suppose that each field operation (addition, subtraction, multiplication, division) has unit cost. This model is called the unit-cost RAM model, which is an ideal abstraction of a computer.
Consider the following problem:
- Input: Three [math]\displaystyle{ n\times n }[/math] matrices [math]\displaystyle{ A }[/math], [math]\displaystyle{ B }[/math], and [math]\displaystyle{ C }[/math] over the field [math]\displaystyle{ \mathbb{F} }[/math].
- Output: "yes" if [math]\displaystyle{ C=AB }[/math] and "no" if otherwise.
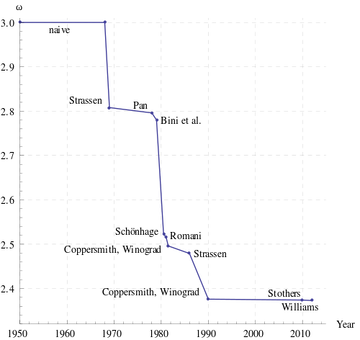
A naive way to solve this is to multiply [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] and compare the result with [math]\displaystyle{ C }[/math]. The straightforward algorithm for matrix multiplication takes [math]\displaystyle{ O(n^3) }[/math] time, assuming that each arithmetic operation takes unit time. The Strassen's algorithm discovered in 1969 now implemented by many numerical libraries runs in time [math]\displaystyle{ O(n^{\log_2 7})\approx O(n^{2.81}) }[/math]. Strassen's algorithm starts the search for fast matrix multiplication algorithms. The Coppersmith–Winograd algorithm discovered in 1987 runs in time [math]\displaystyle{ O(n^{2.376}) }[/math] but is only faster than Strassens' algorithm on extremely large matrices due to the very large constant coefficient. This has been the best known for decades, until recently Stothers got an [math]\displaystyle{ O(n^{2.374}) }[/math] algorithm in his PhD thesis in 2010, and independently Vassilevska Williams got an [math]\displaystyle{ O(n^{2.373}) }[/math] algorithm in 2012. Both these improvements are based on generalization of Coppersmith–Winograd algorithm. It is unknown whether the matrix multiplication can be done in time [math]\displaystyle{ O(n^{2+o(1)}) }[/math].
Freivalds Algorithm
The following is a very simple randomized algorithm due to Freivalds, running in [math]\displaystyle{ O(n^2) }[/math] time:
Algorithm (Freivalds, 1979) - pick a vector [math]\displaystyle{ r \in\{0, 1\}^n }[/math] uniformly at random;
- if [math]\displaystyle{ A(Br) = Cr }[/math] then return "yes" else return "no";
The product [math]\displaystyle{ A(Br) }[/math] is computed by first multiplying [math]\displaystyle{ Br }[/math] and then [math]\displaystyle{ A(Br) }[/math]. The running time of Freivalds algorithm is [math]\displaystyle{ O(n^2) }[/math] because the algorithm computes 3 matrix-vector multiplications.
If [math]\displaystyle{ AB=C }[/math] then [math]\displaystyle{ A(Br) = Cr }[/math] for any [math]\displaystyle{ r \in\{0, 1\}^n }[/math], thus the algorithm will return a "yes" for any positive instance ([math]\displaystyle{ AB=C }[/math]). But if [math]\displaystyle{ AB \neq C }[/math] then the algorithm will make a mistake if it chooses such an [math]\displaystyle{ r }[/math] that [math]\displaystyle{ ABr = Cr }[/math]. However, the following lemma states that the probability of this event is bounded.
Lemma - If [math]\displaystyle{ AB\neq C }[/math] then for a uniformly random [math]\displaystyle{ r \in\{0, 1\}^n }[/math],
- [math]\displaystyle{ \Pr[ABr = Cr]\le \frac{1}{2} }[/math].
- If [math]\displaystyle{ AB\neq C }[/math] then for a uniformly random [math]\displaystyle{ r \in\{0, 1\}^n }[/math],
Proof. Let [math]\displaystyle{ D=AB-C }[/math]. The event [math]\displaystyle{ ABr=Cr }[/math] is equivalent to that [math]\displaystyle{ Dr=0 }[/math]. It is then sufficient to show that for a [math]\displaystyle{ D\neq \boldsymbol{0} }[/math], it holds that [math]\displaystyle{ \Pr[Dr = \boldsymbol{0}]\le \frac{1}{2} }[/math]. Since [math]\displaystyle{ D\neq \boldsymbol{0} }[/math], it must have at least one non-zero entry. Suppose that [math]\displaystyle{ D_{ij}\neq 0 }[/math].
We assume the event that [math]\displaystyle{ Dr=\boldsymbol{0} }[/math]. In particular, the [math]\displaystyle{ i }[/math]-th entry of [math]\displaystyle{ Dr }[/math] is
- [math]\displaystyle{ (Dr)_{i}=\sum_{k=1}^n D_{ik}r_k=0. }[/math]
The [math]\displaystyle{ r_j }[/math] can be calculated by
- [math]\displaystyle{ r_j=-\frac{1}{D_{ij}}\sum_{k\neq j}^n D_{ik}r_k. }[/math]
Once all other entries [math]\displaystyle{ r_k }[/math] with [math]\displaystyle{ k\neq j }[/math] are fixed, there is a unique solution of [math]\displaystyle{ r_j }[/math]. Therefore, the number of [math]\displaystyle{ r\in\{0,1\}^n }[/math] satisfying [math]\displaystyle{ Dr=\boldsymbol{0} }[/math] is at most [math]\displaystyle{ 2^{n-1} }[/math]. The probability that [math]\displaystyle{ ABr=Cr }[/math] is bounded as
- [math]\displaystyle{ \Pr[ABr=Cr]=\Pr[Dr=\boldsymbol{0}]\le\frac{2^{n-1}}{2^n}=\frac{1}{2} }[/math].
- [math]\displaystyle{ \square }[/math]
When [math]\displaystyle{ AB=C }[/math], Freivalds algorithm always returns "yes"; and when [math]\displaystyle{ AB\neq C }[/math], Freivalds algorithm returns "no" with probability at least 1/2.
To improve its accuracy, we can run Freivalds algorithm for [math]\displaystyle{ k }[/math] times, each time with an independent [math]\displaystyle{ r\in\{0,1\}^n }[/math], and return "yes" if and only if all running instances returns "yes".
Freivalds' Algorithm (multi-round) - pick [math]\displaystyle{ k }[/math] vectors [math]\displaystyle{ r_1,r_2,\ldots,r_k \in\{0, 1\}^n }[/math] uniformly and independently at random;
- if [math]\displaystyle{ A(Br_i) = Cr_i }[/math] for all [math]\displaystyle{ i=1,\ldots,k }[/math] then return "yes" else return "no";
If [math]\displaystyle{ AB=C }[/math], then the algorithm returns a "yes" with probability 1. If [math]\displaystyle{ AB\neq C }[/math], then due to the independence, the probability that all [math]\displaystyle{ r_i }[/math] have [math]\displaystyle{ ABr_i=C_i }[/math] is at most [math]\displaystyle{ 2^{-k} }[/math], so the algorithm returns "no" with probability at least [math]\displaystyle{ 1-2^{-k} }[/math]. For any [math]\displaystyle{ 0\lt \epsilon\lt 1 }[/math], choose [math]\displaystyle{ k=\log_2 \frac{1}{\epsilon} }[/math]. The algorithm runs in time [math]\displaystyle{ O(n^2\log_2\frac{1}{\epsilon}) }[/math] and has a one-sided error (false positive) bounded by [math]\displaystyle{ \epsilon }[/math].
Polynomial Identity Testing (PIT)
The Polynomial Identity Testing (PIT) is such a problem: given as input two polynomials, determine whether two polynomials are identical. This problem plays a fundamental role in Computer Science.
First let's consider the following simplified version of Polynomial Identity Testing (PIT) which takes only the single-variate polynomials:
- Input: two polynomials [math]\displaystyle{ P_1, P_2\in\mathbb{F}[x] }[/math] of degree [math]\displaystyle{ d }[/math].
- Output: "yes" if two polynomials are identical, i.e. [math]\displaystyle{ P_1\equiv P_2 }[/math], and "no" if otherwise.
The [math]\displaystyle{ \mathbb{F}[x] }[/math] denote the ring of polynomials over field [math]\displaystyle{ \mathbb{F} }[/math].
Alternatively, we can consider the following equivalent problem:
- Input: a polynomial [math]\displaystyle{ P\in\mathbb{F}[x] }[/math] of degree [math]\displaystyle{ d }[/math].
- Output: "yes" if [math]\displaystyle{ P\equiv 0 }[/math], and "no" if otherwise.
The probalem is trivial if [math]\displaystyle{ P }[/math] is presented in its explicit form [math]\displaystyle{ P(x)=\sum_{i=0}^d a_ix^i }[/math]. But we assume that [math]\displaystyle{ P }[/math] is given in product form or as black box.
A straightforward deterministic algorithm that solves PIT is to query [math]\displaystyle{ d+1 }[/math] points [math]\displaystyle{ P(1),P(2),\ldots,P(d+1) }[/math] and check whether thay are all zero. This can determine whether [math]\displaystyle{ P\equiv 0 }[/math] by interpolation.
We now introduce a simple randomized algorithm for the problem.
Algorithm for PIT - pick [math]\displaystyle{ x\in\{1,2,\ldots,2d\} }[/math] uniformly at random;
- if [math]\displaystyle{ P(x) = 0 }[/math] then return “yes” else return “no”;
This algorithm requires only the evaluation of [math]\displaystyle{ P }[/math] at a single point. And if [math]\displaystyle{ P\equiv 0 }[/math] it is always correct. And if [math]\displaystyle{ P\not\equiv 0 }[/math] then the probability that the algorithm wrongly returns "yes" is bounded as follows.
Theorem - Let [math]\displaystyle{ P\in\mathbb{F}[x] }[/math] be a polynomial of degree [math]\displaystyle{ d }[/math] over the field [math]\displaystyle{ \mathbb{F} }[/math]. Let [math]\displaystyle{ S\subset\mathbb{F} }[/math] be an arbitrary set and [math]\displaystyle{ x\in S }[/math] is chosen uniformly at random from [math]\displaystyle{ S }[/math]. If [math]\displaystyle{ P\not\equiv 0 }[/math] then
- [math]\displaystyle{ \Pr[P(x)=0]\le\frac{d}{|S|}. }[/math]
- Let [math]\displaystyle{ P\in\mathbb{F}[x] }[/math] be a polynomial of degree [math]\displaystyle{ d }[/math] over the field [math]\displaystyle{ \mathbb{F} }[/math]. Let [math]\displaystyle{ S\subset\mathbb{F} }[/math] be an arbitrary set and [math]\displaystyle{ x\in S }[/math] is chosen uniformly at random from [math]\displaystyle{ S }[/math]. If [math]\displaystyle{ P\not\equiv 0 }[/math] then
Proof. A non-zero [math]\displaystyle{ d }[/math]-degree polynomial [math]\displaystyle{ P }[/math] has at most [math]\displaystyle{ d }[/math] distinct roots, thus at most [math]\displaystyle{ d }[/math] members [math]\displaystyle{ x }[/math] of [math]\displaystyle{ S }[/math] satisfy that [math]\displaystyle{ P(x)=0 }[/math]. Therefore, [math]\displaystyle{ \Pr[P(x)=0]\le\frac{d}{|S|} }[/math].
- [math]\displaystyle{ \square }[/math]
By the theorem, the algorithm can distinguish a non-zero polynomial from 0 with probability at least [math]\displaystyle{ 1/2 }[/math]. This is achieved by evaluation of the polynomial at only one point and [math]\displaystyle{ 1+\log_2 d }[/math] many random bits.
Communication Complexity of Equality
The communication complexity is introduced by Andrew Chi-Chih Yao as a model of computation which involves multiple participants, each with partial information of the input.
Assume that there are two entities, say Alice and Bob. Alice has a private input [math]\displaystyle{ a }[/math] and Bob has a private input [math]\displaystyle{ b }[/math]. Together they want to compute a function [math]\displaystyle{ f(a,b) }[/math] by communicating with each other. The communication follows a predefined communication protocol (the "algorithm" in this model) whose logics depends only on the problem [math]\displaystyle{ f }[/math] but not on the inputs. The complexity of a communication protocol is measured by the number of bits communicated between Alice and Bob in the worst case.
The problem of checking identity is formally defined by the function EQ as follows: [math]\displaystyle{ \mathrm{EQ}:\{0,1\}^n\times\{0,1\}^n\rightarrow\{0,1\} }[/math] and for any [math]\displaystyle{ a,b\in\{0,1\}^n }[/math],
- [math]\displaystyle{ \mathrm{EQ}(a,b)= \begin{cases} 1& \mbox{if } a=b,\\ 0& \mbox{otherwise.} \end{cases} }[/math]
A trivial way to solve EQ is to let Bob send his entire input string [math]\displaystyle{ b }[/math] to Alice and let Alice check whether [math]\displaystyle{ a=b }[/math]. This costs [math]\displaystyle{ n }[/math] bits of communications.
It is known that for deterministic communication protocols, this is the best we can get for computing EQ.
Theorem (Yao 1979) - Any deterministic communication protocol computing EQ on two [math]\displaystyle{ n }[/math]-bit strings costs [math]\displaystyle{ n }[/math] bits of communication in the worst-case.
This theorem is much more nontrivial to prove than it looks, because Alice and Bob are allowed to interact with each other in arbitrary ways. The proof of this theorem in Yao's 1979 paper initiates the field of communication complexity.
If the randomness is allowed, we can solve this problem up to a tolerable probabilistic error with significantly less communications. The inputs [math]\displaystyle{ a,b\in\{0,1\}^{n} }[/math] are two strings [math]\displaystyle{ a=a_0a_1\cdots a_{n-1}, b=b_0b_1\cdots b_{n-1} }[/math] of [math]\displaystyle{ n }[/math] bits. Let [math]\displaystyle{ k=\lceil\log_2 (2n)\rceil }[/math] and [math]\displaystyle{ p\in[2^k,2^{k+1}] }[/math] be an arbitrary prime number. (Such a prime [math]\displaystyle{ p }[/math] always exists.) The input strings [math]\displaystyle{ a,b }[/math] can be respectively represented as two polynomials [math]\displaystyle{ f,g\in\mathbb{Z}_p[x] }[/math] such that [math]\displaystyle{ f(x)=\sum_{i=0}^{n-1}a_ix^{i} }[/math] and [math]\displaystyle{ g(x)=\sum_{i=0}^{n-1}b_ix^{i} }[/math] of degree [math]\displaystyle{ n-1 }[/math], where all additions and multiplications are modulo [math]\displaystyle{ p }[/math]. The randomized communication protocol is given as follows:
A randomized protocol for EQ Alice does:
- pick [math]\displaystyle{ r\in[p] }[/math] uniformly at random;
- send [math]\displaystyle{ r }[/math] and [math]\displaystyle{ f(r) }[/math] to Bob;
Upon receiving [math]\displaystyle{ r }[/math] and [math]\displaystyle{ f(r) }[/math] Bob does:
- If [math]\displaystyle{ f(r)= g(r) }[/math] return "yes"; else return "no".
Repeat this protocol for 100 times. The total number of bits to communicate is bounded by [math]\displaystyle{ 200\log_2p=O(\log n) }[/math]. Due to the analysis of the randomized algorithm for PIT, if [math]\displaystyle{ a=b }[/math] the protocol is always correct and if [math]\displaystyle{ a\neq b }[/math] the protocol fails to report a difference with probability less than [math]\displaystyle{ 2^{-100} }[/math].
Schwartz-Zippel Theorem
Now let's move on to the the true form of Polynomial Identity Testing (PIT) which works on multi-variate polynomials:
- Input: two [math]\displaystyle{ n }[/math]-variate polynomials [math]\displaystyle{ f, g\in\mathbb{F}[x_1,x_2,\ldots,x_n] }[/math] of degree [math]\displaystyle{ d }[/math].
- Output: "yes" if [math]\displaystyle{ f\equiv g }[/math], and "no" if otherwise.
The [math]\displaystyle{ \mathbb{F}[x_1,x_2,\ldots,x_n] }[/math] is the ring of multi-variate polynomials over field [math]\displaystyle{ \mathbb{F} }[/math]. The most natural way to represent an [math]\displaystyle{ n }[/math]-variate polynomial of degree [math]\displaystyle{ d }[/math] is to write it as a sum of monomials:
- [math]\displaystyle{ f(x_1,x_2,\ldots,x_n)=\sum_{i_1,i_2,\ldots,i_n\ge 0\atop i_1+i_2+\cdots+i_n\le d}a_{i_1,i_2,\ldots,i_n}x_{1}^{i_1}x_2^{i_2}\cdots x_{n}^{i_n} }[/math].
The degree or total degree of a monomial [math]\displaystyle{ a_{i_1,i_2,\ldots,i_n}x_{1}^{i_1}x_2^{i_2}\cdots x_{n}^{i_n} }[/math] is given by [math]\displaystyle{ i_1+i_2+\cdots+i_n }[/math] and the degree of a polynomial [math]\displaystyle{ f }[/math] is the maximum degree of monomials of nonzero coefficients.
Alternatively, we can consider the following equivalent problem:
- Input: a polynomial [math]\displaystyle{ f\in\mathbb{F}[x_1,x_2,\ldots,x_n] }[/math] of degree [math]\displaystyle{ d }[/math].
- Output: "yes" if [math]\displaystyle{ f\equiv 0 }[/math], and "no" if otherwise.
If [math]\displaystyle{ f }[/math] is written explicitly as a sum of monomials, then the problem is trivial. Again we allow [math]\displaystyle{ f }[/math] to be represented in product form.
Example The Vandermonde matrix [math]\displaystyle{ M=M(x_1,x_2,\ldots,x_n) }[/math] is defined as that [math]\displaystyle{ M_{ij}=x_i^{j-1} }[/math], that is
- [math]\displaystyle{ M=\begin{bmatrix} 1 & x_1 & x_1^2 & \dots & x_1^{n-1}\\ 1 & x_2 & x_2^2 & \dots & x_2^{n-1}\\ 1 & x_3 & x_3^2 & \dots & x_3^{n-1}\\ \vdots & \vdots & \vdots & \ddots &\vdots \\ 1 & x_n & x_n^2 & \dots & x_n^{n-1} \end{bmatrix} }[/math].
Let [math]\displaystyle{ f }[/math] be the polynomial defined as
- [math]\displaystyle{ f(x_1,\ldots,x_n)=\det(M)=\prod_{j\lt i}(x_i-x_j). }[/math]
It is pretty easy to evaluate [math]\displaystyle{ f(x_1,x_2,\ldots,x_n) }[/math] on any particular [math]\displaystyle{ x_1,x_2,\ldots,x_n }[/math], however it is prohibitively expensive to symbolically expand [math]\displaystyle{ f(x_1,\ldots,x_n) }[/math] to its sum-of-monomial form.
Here is a very simple randomized algorithm, due to Schwartz and Zippel.
Randomized algorithm for multi-variate PIT - fix an arbitrary set [math]\displaystyle{ S\subseteq \mathbb{F} }[/math] whose size to be fixed;
- pick [math]\displaystyle{ r_1,r_2,\ldots,r_n\in S }[/math] uniformly and independently at random;
- if [math]\displaystyle{ f(\vec{r})=f(r_1,r_2,\ldots,r_n) = 0 }[/math] then return “yes” else return “no”;
This algorithm requires only the evaluation of [math]\displaystyle{ f }[/math] at a single point [math]\displaystyle{ \vec{r} }[/math]. And if [math]\displaystyle{ f\equiv 0 }[/math] it is always correct.
In the Theorem below, we’ll see that if [math]\displaystyle{ f\not\equiv 0 }[/math] then the algorithm is incorrect with probability at most [math]\displaystyle{ \frac{d}{|S|} }[/math], where [math]\displaystyle{ d }[/math] is the degree of the polynomial [math]\displaystyle{ f }[/math].
Schwartz-Zippel Theorem - Let [math]\displaystyle{ f\in\mathbb{F}[x_1,x_2,\ldots,x_n] }[/math] be a multivariate polynomial of degree [math]\displaystyle{ d }[/math] over a field [math]\displaystyle{ \mathbb{F} }[/math] such that [math]\displaystyle{ f\not\equiv 0 }[/math]. Fix any finite set [math]\displaystyle{ S\subset\mathbb{F} }[/math], and let [math]\displaystyle{ r_1,r_2\ldots,r_n }[/math] be chosen uniformly and independently at random from [math]\displaystyle{ S }[/math]. Then
- [math]\displaystyle{ \Pr[f(r_1,r_2,\ldots,r_n)=0]\le\frac{d}{|S|}. }[/math]
- Let [math]\displaystyle{ f\in\mathbb{F}[x_1,x_2,\ldots,x_n] }[/math] be a multivariate polynomial of degree [math]\displaystyle{ d }[/math] over a field [math]\displaystyle{ \mathbb{F} }[/math] such that [math]\displaystyle{ f\not\equiv 0 }[/math]. Fix any finite set [math]\displaystyle{ S\subset\mathbb{F} }[/math], and let [math]\displaystyle{ r_1,r_2\ldots,r_n }[/math] be chosen uniformly and independently at random from [math]\displaystyle{ S }[/math]. Then
Proof. We prove by induction on [math]\displaystyle{ n }[/math] the number of variables.
For [math]\displaystyle{ n=1 }[/math], assuming that [math]\displaystyle{ f\not\equiv 0 }[/math], due to the fundamental theorem of algebra, the degree-[math]\displaystyle{ d }[/math] polynomial [math]\displaystyle{ f(x) }[/math] has at most [math]\displaystyle{ d }[/math] roots, thus
- [math]\displaystyle{ \Pr[f(r)=0]\le\frac{d}{|S|}. }[/math]
Assume the induction hypothesis for a multi-variate polynomial up to [math]\displaystyle{ n-1 }[/math] variable.
An [math]\displaystyle{ n }[/math]-variate polynomial [math]\displaystyle{ f(x_1,x_2,\ldots,x_n) }[/math] can be represented as
- [math]\displaystyle{ f(x_1,x_2,\ldots,x_n)=\sum_{i=0}^kx_n^{i}f_i(x_1,x_2,\ldots,x_{n-1}) }[/math],
where [math]\displaystyle{ k }[/math] is the largest power of [math]\displaystyle{ x_n }[/math], which means that the degree of [math]\displaystyle{ f_k }[/math] is at most [math]\displaystyle{ d-k }[/math] and [math]\displaystyle{ f_k\not\equiv 0 }[/math].
In particular, we write [math]\displaystyle{ f }[/math] as a sum of two parts:
- [math]\displaystyle{ f(x_1,x_2,\ldots,x_n)=x_n^k f_k(x_1,x_2,\ldots,x_{n-1})+\bar{f}(x_1,x_2,\ldots,x_n) }[/math],
where both [math]\displaystyle{ f_k }[/math] and [math]\displaystyle{ \bar{f} }[/math] are polynomials, such that
- as argued above, the degree of [math]\displaystyle{ f_k }[/math] is at most [math]\displaystyle{ d-k }[/math] and [math]\displaystyle{ f_k\not\equiv 0 }[/math];
- [math]\displaystyle{ \bar{f}(x_1,x_2,\ldots,x_n)=\sum_{i=0}^{k-1}x_n^i f_i(x_1,x_2,\ldots,x_{n-1}) }[/math], thus [math]\displaystyle{ \bar{f}(x_1,x_2,\ldots,x_n) }[/math] has no [math]\displaystyle{ x_n^{k} }[/math] factor in any term.
By the law of total probability, it holds that
- [math]\displaystyle{ \begin{align} &\Pr[f(r_1,r_2,\ldots,r_n)=0]\\ = &\Pr[f(\vec{r})=0\mid f_k(r_1,r_2,\ldots,r_{n-1})=0]\cdot\Pr[f_k(r_1,r_2,\ldots,r_{n-1})=0]\\ &+\Pr[f(\vec{r})=0\mid f_k(r_1,r_2,\ldots,r_{n-1})\neq0]\cdot\Pr[f_k(r_1,r_2,\ldots,r_{n-1})\neq0]. \end{align} }[/math]
Note that [math]\displaystyle{ f_k(r_1,r_2,\ldots,r_{n-1}) }[/math] is a polynomial on [math]\displaystyle{ n-1 }[/math] variables of degree [math]\displaystyle{ d-k }[/math] such that [math]\displaystyle{ f_k\not\equiv 0 }[/math]. By the induction hypothesis, we have
- [math]\displaystyle{ \begin{align} (*) &\qquad &\Pr[f_k(r_1,r_2,\ldots,r_{n-1})=0]\le\frac{d-k}{|S|}. \end{align} }[/math]
For the second case, recall that [math]\displaystyle{ \bar{f}(x_1,\ldots,x_n) }[/math] has no [math]\displaystyle{ x_n^k }[/math] factor in any term, thus the condition [math]\displaystyle{ f_k(r_1,r_2,\ldots,r_{n-1})\neq0 }[/math] guarantees that
- [math]\displaystyle{ f(r_1,\ldots,r_{n-1},x_n)=x_n^k f_k(r_1,r_2,\ldots,r_{n-1})+\bar{f}(r_1,r_2,\ldots,r_{n-1},x_n)=g_{r_1,\ldots,r_{n-1}}(x_n) }[/math]
is a single-variate polynomial such that the degree of [math]\displaystyle{ g_{r_1,\ldots,r_{n-1}}(x_n) }[/math] is [math]\displaystyle{ k }[/math] and [math]\displaystyle{ g_{r_1,\ldots,r_{n-1}}\not\equiv 0 }[/math], for which we already known that the probability [math]\displaystyle{ g_{r_1,\ldots,r_{n-1}}(r_n)=0 }[/math] is at most [math]\displaystyle{ \frac{k}{|S|} }[/math]. Therefore,
- [math]\displaystyle{ \begin{align} (**) &\qquad &\Pr[f(\vec{r})=0\mid f_k(r_1,r_2,\ldots,r_{n-1})\neq0]=\Pr[g_{r_1,\ldots,r_{n-1}}(r_n)=0\mid f_k(r_1,r_2,\ldots,r_{n-1})\neq0]\le\frac{k}{|S|} \end{align} }[/math].
Substituting both [math]\displaystyle{ (*) }[/math] and [math]\displaystyle{ (**) }[/math] back in the total probability, we have
- [math]\displaystyle{ \Pr[f(r_1,r_2,\ldots,r_n)=0] \le\frac{d-k}{|S|}+\frac{k}{|S|}=\frac{d}{|S|}, }[/math]
which proves the theorem.
In above proof, for the second case that [math]\displaystyle{ f_k(r_1,\ldots,r_{n-1})\neq 0 }[/math], we use an "probabilistic arguement" to deal with the random choices in the condition. Here we give a more rigorous proof by enumerating all elementary events in applying the law of total probability. You make your own judgement which proof is better.
By the law of total probability,
- [math]\displaystyle{ \begin{align} &\Pr[f(\vec{r})=0]\\ = &\sum_{x_1,\ldots,x_{n-1}\in S}\Pr[f(\vec{r})=0\mid \forall i\lt n, r_i=x_i]\cdot\Pr[\forall i\lt n, r_i=x_i]\\ = &\sum_{x_1,\ldots,x_{n-1}\in S\atop f_k(x_1,\ldots,x_{n-1})=0}\Pr[f(\vec{r})=0\mid \forall i\lt n, r_i=x_i]\cdot\Pr[\forall i\lt n, r_i=x_i]\\ &+\sum_{x_1,\ldots,x_{n-1}\in S\atop f_k(x_1,\ldots,x_{n-1})\neq0}\Pr[f(\vec{r})=0\mid \forall i\lt n, r_i=x_i]\cdot\Pr[\forall i\lt n, r_i=x_i]\\ \le &\sum_{x_1,\ldots,x_{n-1}\in S\atop f_k(x_1,\ldots,x_{n-1})=0}\Pr[\forall i\lt n, r_i=x_i]\\ &+\sum_{x_1,\ldots,x_{n-1}\in S\atop f_k(x_1,\ldots,x_{n-1})\neq 0}\Pr[f(x_1,\ldots,x_{n-1},r_n)=0\mid \forall i\lt n, r_i=x_i]\cdot\Pr[\forall i\lt n, r_i=x_i]\\ = &\Pr[f_k(r_1,\ldots,r_{n-1})=0]+\sum_{x_1,\ldots,x_{n-1}\in S\atop f_k(x_1,\ldots,x_{n-1})\neq 0}\Pr[f(x_1,\ldots,x_{n-1},r_n)=0]\cdot\Pr[\forall i\lt n, r_i=x_i]. \end{align} }[/math]
We have argued that [math]\displaystyle{ f_k\not\equiv 0 }[/math] and the degree of [math]\displaystyle{ f_k }[/math] is [math]\displaystyle{ d-k }[/math]. By the induction hypothesis, we have
- [math]\displaystyle{ \Pr[f_k(r_1,\ldots,r_{n-1})=0]\le\frac{d-k}{|S|}. }[/math]
And for every fixed [math]\displaystyle{ x_1,\ldots,x_{n-1}\in S }[/math] such that [math]\displaystyle{ f_k(x_1,\ldots,x_{n-1})\neq 0 }[/math], we have argued that [math]\displaystyle{ f(x_1,\ldots,x_{n-1},x_n) }[/math] is a polynomial in [math]\displaystyle{ x_n }[/math] of degree [math]\displaystyle{ k }[/math], thus
- [math]\displaystyle{ \Pr[f(x_1,\ldots,x_{n-1},r_n)=0]\le\frac{k}{|S|}, }[/math]
which holds for all [math]\displaystyle{ x_1,\ldots,x_{n-1}\in S }[/math] such that [math]\displaystyle{ f_k(x_1,\ldots,x_{n-1})\neq 0 }[/math], therefore the weighted average
- [math]\displaystyle{ \sum_{x_1,\ldots,x_{n-1}\in S\atop f_k(x_1,\ldots,x_{n-1})\neq 0}\Pr[f(x_1,\ldots,x_{n-1},r_n)=0]\cdot\Pr[\forall i\lt n, r_i=x_i] \le\frac{k}{|S|}. }[/math]
Substituting these inequalities back to the total probability, we have [math]\displaystyle{ \Pr[f(\vec{r})=0] \le\frac{d-k}{|S|}+\frac{k}{|S|} =\frac{d}{|S|}. }[/math]
- [math]\displaystyle{ \square }[/math]
Fingerprinting
The Freivald's algorithm and Schwartz-Zippel theorem can be abstracted as the following procedure: Suppose we want to compare two items [math]\displaystyle{ Z_1 }[/math] and [math]\displaystyle{ Z_2 }[/math]. Instead of comparing them directly, we compute random fingerprints [math]\displaystyle{ \mathrm{FING}(Z_1) }[/math] and [math]\displaystyle{ \mathrm{FING}(Z_2) }[/math] of them and compare the fingerprints. The fingerprints has the following properties:
- [math]\displaystyle{ \mathrm{FING}(\cdot) }[/math] is a function, so if [math]\displaystyle{ Z_1= Z_2 }[/math] then [math]\displaystyle{ \mathrm{FING}(Z_1)=\mathrm{FING}(Z_2) }[/math].
- If [math]\displaystyle{ Z_1\neq Z_2 }[/math] then [math]\displaystyle{ \Pr[\mathrm{FING}(Z_1)=\mathrm{FING}(Z_2)] }[/math] is small.
- It is much easier to compute and compare the fingerprints than to compare [math]\displaystyle{ Z_1 }[/math] and [math]\displaystyle{ Z_2 }[/math] directly.
In Freivald's algorithm, the items to compare are two [math]\displaystyle{ n\times n }[/math] matrices [math]\displaystyle{ AB }[/math] and [math]\displaystyle{ C }[/math], and given an [math]\displaystyle{ n\times n }[/math] matrix [math]\displaystyle{ M }[/math], its random fingerprint is computed as [math]\displaystyle{ \mathrm{FING}(M)=Mr }[/math] for a uniformly random [math]\displaystyle{ r\in\{0,1\}^n }[/math].
In Schwartz-Zippel theorem, the items to compare are two polynomials [math]\displaystyle{ P_1(x_1,\ldots,x_n) }[/math] and [math]\displaystyle{ P_2(x_1,\ldots,x_n) }[/math], and given a polynomial [math]\displaystyle{ Q(x_1,\ldots,x_n) }[/math], its random fingerprint is computed as [math]\displaystyle{ \mathrm{FING}(Q)=Q(r_1,\ldots,r_n) }[/math] for [math]\displaystyle{ r_i }[/math] chosen independently and uniformly at random from some fixed set [math]\displaystyle{ S }[/math].
For different problems, we may have different definitions of [math]\displaystyle{ \mathrm{FING}(\cdot) }[/math].
Communication complexity revisited
Now consider again the communication model where the two players Alice with a private input [math]\displaystyle{ x\in\{0,1\}^n }[/math] and Bob with a private input [math]\displaystyle{ y\in\{0,1\}^n }[/math] together compute a function [math]\displaystyle{ f(x,y) }[/math] by running a communication protocol.
We still consider the communication protocols for the equality function EQ
- [math]\displaystyle{ \mathrm{EQ}(x,y)= \begin{cases} 1& \mbox{if } x=y,\\ 0& \mbox{otherwise.} \end{cases} }[/math]
With the language of fingerprinting, this communication problem can be solved by the following generic scheme:
- Alice choose a random fingerprint function [math]\displaystyle{ \mathrm{FING}(\cdot) }[/math] and compute the fingerprint of her input [math]\displaystyle{ \mathrm{FING}(x) }[/math];
- Alice sends both the description of [math]\displaystyle{ \mathrm{FING}(\cdot) }[/math] and the value of [math]\displaystyle{ \mathrm{FING}(x) }[/math] to Bob;
- Bob computes [math]\displaystyle{ \mathrm{FING}(y) }[/math] and check whether [math]\displaystyle{ \mathrm{FING}(x)=\mathrm{FING}(y) }[/math].
In this way we have a randomized communication protocol for the equality function EQ with a false positive. The communication cost as well as the error probability are reduced to the question of how to design this random fingerprint function [math]\displaystyle{ \mathrm{FING}(\cdot) }[/math] to guarantee:
- A random [math]\displaystyle{ \mathrm{FING}(\cdot) }[/math] can be described succinctly.
- The range of [math]\displaystyle{ \mathrm{FING}(\cdot) }[/math] is small, so the fingerprints are succinct.
- If [math]\displaystyle{ x\neq y }[/math], the probability [math]\displaystyle{ \Pr[\mathrm{FING}(x)=\mathrm{FING}(y)] }[/math] is small.
In above application of single-variate PIT, we know that [math]\displaystyle{ \mathrm{FING}(x)=\sum_{i=1}^n x_i r^{i} }[/math], where [math]\displaystyle{ r }[/math] is a random element from a finite field and the additions and multiplications are defined over the finite field, is a good fingerprint function. Now we introduce another fingerprint and hence a new communication protocol.
The new fingerprint function we design is as follows: by treating the input string [math]\displaystyle{ x\in\{0,1\}^n }[/math] as the binary representation of a number, let [math]\displaystyle{ \mathrm{FING}(x)=x\bmod p }[/math] for some random prime [math]\displaystyle{ p }[/math]. The prime [math]\displaystyle{ p }[/math] can uniquely specify a random fingerprint function [math]\displaystyle{ \mathrm{FING}(\cdot) }[/math], thus can be used as a description of the function, and alos the range of the fingerprints is [math]\displaystyle{ [p] }[/math], thus we want the prime [math]\displaystyle{ p }[/math] to be reasonably small, but still has a good chance to distinguish different [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] after modulo [math]\displaystyle{ p }[/math].
A randomized protocol for EQ Alice does:
- for some parameter [math]\displaystyle{ k }[/math] (to be specified),
- choose uniformly at random a prime [math]\displaystyle{ p\in[k] }[/math];
- send [math]\displaystyle{ p }[/math] and [math]\displaystyle{ x\bmod p }[/math] to Bob;
Upon receiving [math]\displaystyle{ p }[/math] and [math]\displaystyle{ x\bmod p }[/math], Bob does:
- check whether [math]\displaystyle{ x\bmod p=y\bmod p }[/math].
- for some parameter [math]\displaystyle{ k }[/math] (to be specified),
The number of bits to be communicated is [math]\displaystyle{ O(\log k) }[/math]. We then bound the probability of error [math]\displaystyle{ \Pr[x\bmod p=y\bmod p] }[/math] for [math]\displaystyle{ x\neq y }[/math], in terms of [math]\displaystyle{ k }[/math].
Suppose without loss of generality [math]\displaystyle{ x\gt y }[/math]. Let [math]\displaystyle{ z=x-y }[/math]. Then [math]\displaystyle{ z\lt 2^n }[/math] since [math]\displaystyle{ x,y\in[2^n] }[/math], and [math]\displaystyle{ z\neq 0 }[/math] for [math]\displaystyle{ x\neq y }[/math]. It holds that [math]\displaystyle{ x\bmod p=y\bmod p }[/math] if and only if [math]\displaystyle{ z }[/math] is dividable by [math]\displaystyle{ p }[/math]. Note that [math]\displaystyle{ z\lt 2^n }[/math] since [math]\displaystyle{ x,y\in[2^n] }[/math]. We only need to bound the probability
- [math]\displaystyle{ \Pr[z\bmod p=0] }[/math] for [math]\displaystyle{ 0\lt z\lt 2^n }[/math], where [math]\displaystyle{ p }[/math] is a random prime chosen from [math]\displaystyle{ [k] }[/math].
The probability [math]\displaystyle{ \Pr[z\bmod p=0] }[/math] is computed directly as
- [math]\displaystyle{ \Pr[z\bmod p=0]\le\frac{\mbox{the number of prime divisors of }z}{\mbox{the number of primes in }[k]} }[/math].
For the numerator, we have the following lemma.
Lemma - The number of distinct prime divisors of any natural number less than [math]\displaystyle{ 2^n }[/math] is at most [math]\displaystyle{ n }[/math].
Proof. Each prime number is [math]\displaystyle{ \ge2 }[/math]. If an [math]\displaystyle{ N\gt 0 }[/math] has more than [math]\displaystyle{ n }[/math] distinct prime divisors, then [math]\displaystyle{ N\ge 2^n }[/math].
- [math]\displaystyle{ \square }[/math]
Due to this lemma, [math]\displaystyle{ z }[/math] has at most [math]\displaystyle{ n }[/math] prime divisors.
We then lower bound the number of primes in [math]\displaystyle{ [k] }[/math]. This is given by the celebrated Prime Number Theorem (PNT).
Prime Number Theorem - Let [math]\displaystyle{ \pi(k) }[/math] denote the number of primes less than [math]\displaystyle{ k }[/math]. Then [math]\displaystyle{ \pi(k)\sim\frac{k}{\ln k} }[/math] as [math]\displaystyle{ k\rightarrow\infty }[/math].
Therefore, by choosing [math]\displaystyle{ k=tn\ln tn }[/math] for some [math]\displaystyle{ t }[/math], we have that for a [math]\displaystyle{ 0\lt z\lt 2^n }[/math], and a random prime [math]\displaystyle{ p\in[k] }[/math],
- [math]\displaystyle{ \Pr[z\bmod p=0]\le\frac{n}{\pi(k)}\sim\frac{1}{t} }[/math].
We can make this error probability polynomially small and the number of bits to be communicated is still [math]\displaystyle{ O(\log k)=O(\log n) }[/math].
Randomized pattern matching
Consider the following problem of pattern matching, which has nothing to do with communication complexity.
- Input: a string [math]\displaystyle{ x\in\{0,1\}^n }[/math] and a "pattern" [math]\displaystyle{ y\in\{0,1\}^m }[/math].
- Determine whether the pattern [math]\displaystyle{ y }[/math] is a contiguous substring of [math]\displaystyle{ x }[/math]. Usually, we are also asked to find the location of the substring.
A naive algorithm trying every possible match runs in [math]\displaystyle{ O(nm) }[/math] time. The more sophisticated KMP algorithm inspired by automaton theory runs in [math]\displaystyle{ O(n+m) }[/math] time.
A simple randomized algorithm, due to Karp and Rabin, uses the idea of fingerprinting and also runs in [math]\displaystyle{ O(n + m) }[/math] time.
Let [math]\displaystyle{ X(j)=x_jx_{j+1}\cdots x_{j+m-1} }[/math] denote the substring of [math]\displaystyle{ x }[/math] of length [math]\displaystyle{ m }[/math] starting at position [math]\displaystyle{ j }[/math].
Algorithm (Karp-Rabin) - pick a random prime [math]\displaystyle{ p\in[k] }[/math];
- for [math]\displaystyle{ j = 1 }[/math] to [math]\displaystyle{ n -m + 1 }[/math] do
- if [math]\displaystyle{ X(j)\bmod p = y \bmod p }[/math] then report a match;
- return "no match";
So the algorithm just compares the [math]\displaystyle{ \mathrm{FING}(X(j)) }[/math] and [math]\displaystyle{ \mathrm{FING}(y) }[/math] for every [math]\displaystyle{ j }[/math], with the same definition of fingerprint function [math]\displaystyle{ \mathrm{FING}(\cdot) }[/math] as in the communication protocol for EQ.
By the same analysis, by choosing [math]\displaystyle{ k=n^2m\ln (n^2m) }[/math], the probability of a single false match is
- [math]\displaystyle{ \Pr[X(j)\bmod p=y\bmod p\mid X(j)\neq y ]=O\left(\frac{1}{n^2}\right) }[/math].
By the union bound, the probability that a false match occurs is [math]\displaystyle{ O\left(\frac{1}{n}\right) }[/math].
The algorithm runs in linear time if we assume that we can compute [math]\displaystyle{ X(j)\bmod p }[/math] for each [math]\displaystyle{ j }[/math] in constant time. This outrageous assumption can be made realistic by the following observation.
Lemma - Let [math]\displaystyle{ \mathrm{FING}(a)=a\bmod p }[/math].
- [math]\displaystyle{ \mathrm{FING}(X(j+1))\equiv2(\mathrm{FING}(X(j))-2^{m-1}x_j)+x_{j+m}\pmod p\, }[/math].
- Let [math]\displaystyle{ \mathrm{FING}(a)=a\bmod p }[/math].
Proof. It holds that - [math]\displaystyle{ X(j+1)=2(X(j)-2^{m-1}x_j)+x_{j+m}\, }[/math].
So the equation holds on the finite field modulo [math]\displaystyle{ p }[/math].
- [math]\displaystyle{ \square }[/math]
Due to this lemma, each fingerprint [math]\displaystyle{ \mathrm{FING}(X(j)) }[/math] can be computed in an incremental way, each in constant time. The running time of the algorithm is [math]\displaystyle{ O(n+m) }[/math].