随机算法 (Spring 2013)/Introduction and Probability Space
Introduction
This course will study Randomized Algorithms, the algorithms that use randomness in computation.
- Why do we use randomness in computation?
- Randomized algorithms can be simpler than deterministic ones.
- (median selection, load balancing, etc.)
- Randomized algorithms can be faster than the best known deterministic algorithms.
- (min-cut, checking matrix multiplication, primality testing, etc.)
- Randomized algorithms can do things that deterministic algorithms cannot do.
- (routing, volume estimation, communication complexity, data streams, etc.)
- Randomized algorithms may lead us to smart deterministic algorithms.
- (hashing, derandomization, SL=L, Lovász Local Lemma, etc.)
- Randomness is presented in the input.
- (average-case analysis, smoothed analysis, learning, etc.)
- Some deterministic problems are random in nature.
- (counting, inference, etc.)
- ...
- How is randomness used in computation?
- To hit a witness/certificate.
- (identity testing, fingerprinting, primality testing, etc.)
- To avoid worst case or to deal with adversaries.
- (randomized quick sort, perfect hashing, etc.)
- To simulate random samples.
- (random walk, Markov chain Monte Carlo, approximate counting etc.)
- To enumerate/construct solutions.
- (the probabilistic method, min-cut, etc.)
- To break symmetry.
- (mutual exclusion, leader election, parrallel/distributed algorithms, etc.)
- ...
Principles in probability theory
The course is organized by the advancedness of the probabilistic tools. We do this for two reasons: First, for randomized algorithms, analysis is usually more difficult and involved than the algorithm itself; and second, getting familiar with these probability principles will help you understand the true reasons for which the smart algorithms are designed.
- Basics of probability theory: probability space, events, the union bound, independence, conditional probability.
- Moments and deviations: random variables, expectation, linearity of expectation, Markov's inequality, variance, second moment method.
- The probabilistic method: averaging principle, threshold phenomena, Lovász Local Lemma.
- Concentrations: Chernoff-Hoeffding bound, martingales, Azuma's inequality, bounded difference method.
- Markov chains and random walks: Markov chians, random walks, hitting/cover time, mixing time, coupling, conductance.
Probability Space
The axiom foundation of probability theory is laid by Kolmogorov, one of the greatest mathematician of the 20th century, who advanced various very different fields of mathematics.
Definition (Probability Space) A probability space is a triple [math]\displaystyle{ (\Omega,\Sigma,\Pr) }[/math].
- [math]\displaystyle{ \Omega }[/math] is a set, called the sample space.
- [math]\displaystyle{ \Sigma\subseteq 2^{\Omega} }[/math] is the set of all events, satisfying:
- (K1). [math]\displaystyle{ \Omega\in\Sigma }[/math] and [math]\displaystyle{ \empty\in\Sigma }[/math]. (The certain event and the impossible event.)
- (K2). If [math]\displaystyle{ A,B\in\Sigma }[/math], then [math]\displaystyle{ A\cap B, A\cup B, A-B\in\Sigma }[/math]. (Intersection, union, and diference of two events are events).
- A probability measure [math]\displaystyle{ \Pr:\Sigma\rightarrow\mathbb{R} }[/math] is a function that maps each event to a nonnegative real number, satisfying
- (K3). [math]\displaystyle{ \Pr(\Omega)=1 }[/math].
- (K4). If [math]\displaystyle{ A\cap B=\emptyset }[/math] (such events are call disjoint events), then [math]\displaystyle{ \Pr(A\cup B)=\Pr(A)+\Pr(B) }[/math].
- (K5*). For a decreasing sequence of events [math]\displaystyle{ A_1\supset A_2\supset \cdots\supset A_n\supset\cdots }[/math] of events with [math]\displaystyle{ \bigcap_n A_n=\emptyset }[/math], it holds that [math]\displaystyle{ \lim_{n\rightarrow \infty}\Pr(A_n)=0 }[/math].
- Remark
- In general, the set [math]\displaystyle{ \Omega }[/math] may be continuous, but we only consider discrete probability in this lecture, thus we assume that [math]\displaystyle{ \Omega }[/math] is either finite or countably infinite.
- Sometimes it is convenient to assume [math]\displaystyle{ \Sigma=2^{\Omega} }[/math], i.e. the events enumerates all subsets of [math]\displaystyle{ \Omega }[/math]. But in general, a probability space is well-defined by any [math]\displaystyle{ \Sigma }[/math] satisfying (K1) and (K2). Such [math]\displaystyle{ \Sigma }[/math] is called a [math]\displaystyle{ \sigma }[/math]-algebra defined on [math]\displaystyle{ \Omega }[/math].
- The last axiom (K5*) is redundant if [math]\displaystyle{ \Sigma }[/math] is finite, thus it is only essential when there are infinitely many events. The role of axiom (K5*) in probability theory is like Zorn's Lemma (or equivalently the Axiom of Choice) in axiomatic set theory.
Useful laws for probability can be deduced from the axioms (K1)-(K5).
Proposition - Let [math]\displaystyle{ \bar{A}=\Omega\setminus A }[/math]. It holds that [math]\displaystyle{ \Pr(\bar{A})=1-\Pr(A) }[/math].
- If [math]\displaystyle{ A\subseteq B }[/math] then [math]\displaystyle{ \Pr(A)\le\Pr(B) }[/math].
Proof. - The events [math]\displaystyle{ \bar{A} }[/math] and [math]\displaystyle{ A }[/math] are disjoint and [math]\displaystyle{ \bar{A}\cup A=\Omega }[/math]. Due to Axiom (K4) and (K3), [math]\displaystyle{ \Pr(\bar{A})+\Pr(A)=\Pr(\Omega)=1 }[/math].
- The events [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B\setminus A }[/math] are disjoint and [math]\displaystyle{ A\cup(B\setminus A)=B }[/math] since [math]\displaystyle{ A\subseteq B }[/math]. Due to Axiom (K4), [math]\displaystyle{ \Pr(A)+\Pr(B\setminus A)=\Pr(B) }[/math], thus [math]\displaystyle{ \Pr(A)\le\Pr(B) }[/math].
- [math]\displaystyle{ \square }[/math]
- Notation
An event [math]\displaystyle{ A\subseteq\Omega }[/math] can be represented as [math]\displaystyle{ A=\{a\in\Omega\mid \mathcal{E}(a)\} }[/math] with a predicate [math]\displaystyle{ \mathcal{E} }[/math].
The predicate notation of probability is
- [math]\displaystyle{ \Pr[\mathcal{E}]=\Pr(\{a\in\Omega\mid \mathcal{E}(a)\}) }[/math].
During the lecture, we mostly use the predicate notation instead of subset notation.
Independence
Definition (Independent events) - Two events [math]\displaystyle{ \mathcal{E}_1 }[/math] and [math]\displaystyle{ \mathcal{E}_2 }[/math] are independent if and only if
- [math]\displaystyle{ \begin{align} \Pr\left[\mathcal{E}_1 \wedge \mathcal{E}_2\right] &= \Pr[\mathcal{E}_1]\cdot\Pr[\mathcal{E}_2]. \end{align} }[/math]
- Two events [math]\displaystyle{ \mathcal{E}_1 }[/math] and [math]\displaystyle{ \mathcal{E}_2 }[/math] are independent if and only if
This definition can be generalized to any number of events:
Definition (Independent events) - Events [math]\displaystyle{ \mathcal{E}_1, \mathcal{E}_2, \ldots, \mathcal{E}_n }[/math] are mutually independent if and only if, for any subset [math]\displaystyle{ I\subseteq\{1,2,\ldots,n\} }[/math],
- [math]\displaystyle{ \begin{align} \Pr\left[\bigwedge_{i\in I}\mathcal{E}_i\right] &= \prod_{i\in I}\Pr[\mathcal{E}_i]. \end{align} }[/math]
- Events [math]\displaystyle{ \mathcal{E}_1, \mathcal{E}_2, \ldots, \mathcal{E}_n }[/math] are mutually independent if and only if, for any subset [math]\displaystyle{ I\subseteq\{1,2,\ldots,n\} }[/math],
Note that in probability theory, the "mutual independence" is not equivalent with "pair-wise independence", which we will learn in the future.
Model of Computation
Our model of computation extends the standard model (Turing machine or random-access machine) with access to uniform and independent random bits (fair coin flips). On a fixed input, the behavior of the algorithm is random. To be specific, the output or running time of the algorithm may be random.
Monte Carlo algorithms
Monte Carlo algorithms always returns in finite steps but may output the wrong answer. For decision problems (problems with two answers "yes" and "no"), the Monte Carlo algorithms are further divided into those with one-sided errors and two-sided errors.
- Monte Carlo algorithms with one-sided errors
- These algorithms only make errors in one direction, which may be further divided into two cases:
- False positive: If the true answer is "yes" then the algorithm returns "yes" with probability 1, and if the true answer is "no" then the algorithm returns "no" with probability at least [math]\displaystyle{ \epsilon }[/math], where [math]\displaystyle{ 0\lt \epsilon\lt 1 }[/math] is the confidence. The algorithm may return a wrong "yes" while the true answer is "no".
- The one-sided error can be reduced by independent repetitions. Run the algorithm independently for [math]\displaystyle{ t }[/math] times, output "yes" if all running instances return "yes", and output "no" if otherwise. If the true answer is "yes" this new algorithm returns "yes" since all running instances are guaranteed to do so, and if the true answer is "no" the new algorithm returns "yes" only if all running instances return "yes", whose probability is bounded by [math]\displaystyle{ (1-\epsilon)^t }[/math], which can be reduced to any [math]\displaystyle{ \delta\in(0,1) }[/math] by setting [math]\displaystyle{ t=O\left(\frac{1}{\epsilon}\log\frac{1}{\delta}\right) }[/math].
- False negative: If the true answer is "yes" then the algorithm returns "yes" with probability at least [math]\displaystyle{ \epsilon }[/math], and if the true answer is "no" then the algorithm returns "no" with probability 1. The algorithm may return a wrong "no" while the true answer is "yes". The error can be reduced in the same way.
- Monte Carlo algorithms with two-sided errors
- These algorithms make errors in both directions. If the true answer is "yes" then the algorithm returns "yes" with probability at least [math]\displaystyle{ \frac{1}{2}+\epsilon }[/math], and if the true answer is "no" then the algorithm returns "no" with probability at least [math]\displaystyle{ \frac{1}{2}+\epsilon }[/math], where [math]\displaystyle{ \epsilon\in \left(0,\frac{1}{2}\right) }[/math] is a bias.
- The error can be reduced by repetitions and majority vote. Run the algorithm independently for [math]\displaystyle{ t }[/math] times, output "yes" if over half running instances return "yes", and output "no" if otherwise. The numbers of "yes"s and "no"s in the [math]\displaystyle{ t }[/math] trials follow the Binomial distribution. For each [math]\displaystyle{ 0\le i\le t }[/math], the probability that there are precisely [math]\displaystyle{ i }[/math] correct answers in [math]\displaystyle{ t }[/math] trials is given by
- [math]\displaystyle{ {t\choose i}\left(\frac{1}{2}+\epsilon\right)^i\left(\frac{1}{2}-\epsilon\right)^{t-i}, }[/math]
- and the new algorithm returns a wrong answer only if at most [math]\displaystyle{ \lfloor t/2\rfloor }[/math] correct answers in [math]\displaystyle{ t }[/math] trials, which is given by
- [math]\displaystyle{ \begin{align} \sum_{i=0}^{\lfloor t/2\rfloor} {t\choose i}\left(\frac{1}{2}+\epsilon\right)^i\left(\frac{1}{2}-\epsilon\right)^{t-i} &\le \sum_{i=0}^{\lfloor t/2\rfloor} {t\choose i}\left(\frac{1}{2}+\epsilon\right)^{t/2}\left(\frac{1}{2}-\epsilon\right)^{t/2}\\ &= \left(\frac{1}{4}-\epsilon^2\right)^{t/2}\sum_{i=0}^{\lfloor t/2\rfloor}{t\choose i}\\ &\le \left(\frac{1}{4}-\epsilon^2\right)^{t/2}2^t\\ &=(1-4\epsilon^2)^{t/2}, \end{align} }[/math]
- which can be reduced to any [math]\displaystyle{ \delta\in(0,1) }[/math] by setting [math]\displaystyle{ t=O\left(\frac{1}{\epsilon^2}\log\frac{1}{\delta}\right) }[/math].
Las Vegas algorithms
Las Vegas algorithms always output correct answers but the running time is random. The time complexity of a Las Vegas algorithm is measure by the expected running time. The concept of Las Vegas algorithm is introduced by Babai in 1979 in his seminal work on graph isomorphsm testing.
A Las Vegas algorithm can be converted to a Monte Carlo algorithm by truncating. The error of the resulting Monte Carlo algorithm can be made one-sided and can be bounded by Markov's inequality. There is no general way known to convert a Monte Carlo algorithm to a Las Vegas algorithm.
Checking Matrix Multiplication
Let [math]\displaystyle{ \mathbb{F} }[/math] be a feild (you may think of it as the filed [math]\displaystyle{ \mathbb{Q} }[/math] of rational numbers, or the finite field [math]\displaystyle{ \mathbb{Z}_p }[/math] of integers modulo prime [math]\displaystyle{ p }[/math]). We suppose that each field operation (addition, subtraction, multiplication, division) has unit cost. This model is called the unit-cost RAM model, which is an ideal abstraction of a computer.
Consider the following problem:
- Input: Three [math]\displaystyle{ n\times n }[/math] matrices [math]\displaystyle{ A }[/math], [math]\displaystyle{ B }[/math], and [math]\displaystyle{ C }[/math] over the field [math]\displaystyle{ \mathbb{F} }[/math].
- Output: "yes" if [math]\displaystyle{ C=AB }[/math] and "no" if otherwise.
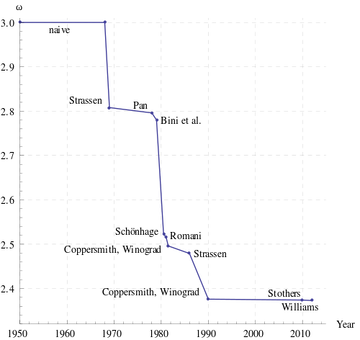
A naive way to solve this is to multiply [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] and compare the result with [math]\displaystyle{ C }[/math]. The straightforward algorithm for matrix multiplication takes [math]\displaystyle{ O(n^3) }[/math] time, assuming that each arithmetic operation takes unit time. The Strassen's algorithm discovered in 1969 now implemented by many numerical libraries runs in time [math]\displaystyle{ O(n^{\log_2 7})\approx O(n^{2.81}) }[/math]. Strassen's algorithm starts the search for fast matrix multiplication algorithms. The Coppersmith–Winograd algorithm discovered in 1987 runs in time [math]\displaystyle{ O(n^{2.376}) }[/math] but is only faster than Strassens' algorithm on extremely large matrices due to the very large constant coefficient. This has been the best known for decades, until recently Stothers got an [math]\displaystyle{ O(n^{2.3737}) }[/math] algorithm in his PhD thesis in 2010, and independently Vassilevska Williams got an [math]\displaystyle{ O(n^{2.3727}) }[/math] algorithm in 2012. Both these improvements are based on generalization of Coppersmith–Winograd algorithm. It is unknown whether the matrix multiplication can be done in time [math]\displaystyle{ O(n^{2+o(1)}) }[/math].
Freivalds Algorithm
The following is a very simple randomized algorithm due to Freivalds, running in [math]\displaystyle{ O(n^2) }[/math] time:
Algorithm (Freivalds, 1979) - pick a vector [math]\displaystyle{ r \in\{0, 1\}^n }[/math] uniformly at random;
- if [math]\displaystyle{ A(Br) = Cr }[/math] then return "yes" else return "no";
The product [math]\displaystyle{ A(Br) }[/math] is computed by first multiplying [math]\displaystyle{ Br }[/math] and then [math]\displaystyle{ A(Br) }[/math]. The running time of Freivalds algorithm is [math]\displaystyle{ O(n^2) }[/math] because the algorithm computes 3 matrix-vector multiplications.
If [math]\displaystyle{ AB=C }[/math] then [math]\displaystyle{ A(Br) = Cr }[/math] for any [math]\displaystyle{ r \in\{0, 1\}^n }[/math], thus the algorithm will return a "yes" for any positive instance ([math]\displaystyle{ AB=C }[/math]). But if [math]\displaystyle{ AB \neq C }[/math] then the algorithm will make a mistake if it chooses such an [math]\displaystyle{ r }[/math] that [math]\displaystyle{ ABr = Cr }[/math]. However, the following lemma states that the probability of this event is bounded.
Lemma - If [math]\displaystyle{ AB\neq C }[/math] then for a uniformly random [math]\displaystyle{ r \in\{0, 1\}^n }[/math],
- [math]\displaystyle{ \Pr[ABr = Cr]\le \frac{1}{2} }[/math].
- If [math]\displaystyle{ AB\neq C }[/math] then for a uniformly random [math]\displaystyle{ r \in\{0, 1\}^n }[/math],
Proof. Let [math]\displaystyle{ D=AB-C }[/math]. The event [math]\displaystyle{ ABr=Cr }[/math] is equivalent to that [math]\displaystyle{ Dr=0 }[/math]. It is then sufficient to show that for a [math]\displaystyle{ D\neq \boldsymbol{0} }[/math], it holds that [math]\displaystyle{ \Pr[Dr = \boldsymbol{0}]\le \frac{1}{2} }[/math]. Since [math]\displaystyle{ D\neq \boldsymbol{0} }[/math], it must have at least one non-zero entry. Suppose that [math]\displaystyle{ D_{ij}\neq 0 }[/math].
We assume the event that [math]\displaystyle{ Dr=\boldsymbol{0} }[/math]. In particular, the [math]\displaystyle{ i }[/math]-th entry of [math]\displaystyle{ Dr }[/math] is
- [math]\displaystyle{ (Dr)_{i}=\sum_{k=1}^n D_{ik}r_k=0. }[/math]
The [math]\displaystyle{ r_j }[/math] can be calculated by
- [math]\displaystyle{ r_j=-\frac{1}{D_{ij}}\sum_{k\neq j}^n D_{ik}r_k. }[/math]
Once all other entries [math]\displaystyle{ r_k }[/math] with [math]\displaystyle{ k\neq j }[/math] are fixed, there is a unique solution of [math]\displaystyle{ r_j }[/math]. Therefore, the number of [math]\displaystyle{ r\in\{0,1\}^n }[/math] satisfying [math]\displaystyle{ Dr=\boldsymbol{0} }[/math] is at most [math]\displaystyle{ 2^{n-1} }[/math]. The probability that [math]\displaystyle{ ABr=Cr }[/math] is bounded as
- [math]\displaystyle{ \Pr[ABr=Cr]=\Pr[Dr=\boldsymbol{0}]\le\frac{2^{n-1}}{2^n}=\frac{1}{2} }[/math].
- [math]\displaystyle{ \square }[/math]
When [math]\displaystyle{ AB=C }[/math], Freivalds algorithm always returns "yes"; and when [math]\displaystyle{ AB\neq C }[/math], Freivalds algorithm returns "no" with probability at least 1/2.
To improve its accuracy, we can run Freivalds algorithm for [math]\displaystyle{ k }[/math] times, each time with an independent [math]\displaystyle{ r\in\{0,1\}^n }[/math], and return "yes" if and only if all running instances returns "yes".
Freivalds' Algorithm (multi-round) - pick [math]\displaystyle{ k }[/math] vectors [math]\displaystyle{ r_1,r_2,\ldots,r_k \in\{0, 1\}^n }[/math] uniformly and independently at random;
- if [math]\displaystyle{ A(Br_i) = Cr_i }[/math] for all [math]\displaystyle{ i=1,\ldots,k }[/math] then return "yes" else return "no";
If [math]\displaystyle{ AB=C }[/math], then the algorithm returns a "yes" with probability 1. If [math]\displaystyle{ AB\neq C }[/math], then due to the independence, the probability that all [math]\displaystyle{ r_i }[/math] have [math]\displaystyle{ ABr_i=C_i }[/math] is at most [math]\displaystyle{ 2^{-k} }[/math], so the algorithm returns "no" with probability at least [math]\displaystyle{ 1-2^{-k} }[/math]. For any [math]\displaystyle{ 0\lt \epsilon\lt 1 }[/math], choose [math]\displaystyle{ k=\log_2 \frac{1}{\epsilon} }[/math]. The algorithm runs in time [math]\displaystyle{ O(n^2\log_2\frac{1}{\epsilon}) }[/math] and has a one-sided error (false positive) bounded by [math]\displaystyle{ \epsilon }[/math].
Polynomial Identity Testing (PIT)
Consider the following problem of Polynomial Identity Testing (PIT):
- Input: two polynomials [math]\displaystyle{ P_1, P_2\in\mathbb{F}[x] }[/math] of degree [math]\displaystyle{ d }[/math].
- Output: "yes" if two polynomials are identical, i.e. [math]\displaystyle{ P_1\equiv P_2 }[/math], and "no" if otherwise.
The [math]\displaystyle{ \mathbb{F}[x] }[/math] denote the ring of polynomials over field [math]\displaystyle{ \mathbb{F} }[/math].
Alternatively, we can consider the following equivalent problem:
- Input: a polynomial [math]\displaystyle{ P\in\mathbb{F}[x] }[/math] of degree [math]\displaystyle{ d }[/math].
- Output: "yes" if [math]\displaystyle{ P\equiv 0 }[/math], and "no" if otherwise.
The probalem is trivial if [math]\displaystyle{ P }[/math] is presented in its explicit form [math]\displaystyle{ P(x)=\sum_{i=0}^d a_ix^i }[/math]. But we assume that [math]\displaystyle{ P }[/math] is given in product form or as black box.
A straightforward deterministic algorithm that solves PIT is to query [math]\displaystyle{ d+1 }[/math] points [math]\displaystyle{ P(1),P(2),\ldots,P(d+1) }[/math] and check whether thay are all zero. This can determine whether [math]\displaystyle{ P\equiv 0 }[/math] by interpolation.
We now introduce a simple randomized algorithm for the problem.
Algorithm for PIT - pick [math]\displaystyle{ x\in\{1,2,\ldots,2d\} }[/math] uniformly at random;
- if [math]\displaystyle{ P(x) = 0 }[/math] then return “yes” else return “no”;
This algorithm requires only the evaluation of [math]\displaystyle{ P }[/math] at a single point. And if [math]\displaystyle{ P\equiv 0 }[/math] it is always correct. And if [math]\displaystyle{ P\not\equiv 0 }[/math] then the probability that the algorithm wrongly returns "yes" is bounded as follows.
Theorem - Let [math]\displaystyle{ P\in\mathbb{F}[x] }[/math] be a polynomial of degree [math]\displaystyle{ d }[/math] over the field [math]\displaystyle{ \mathbb{F} }[/math]. Let [math]\displaystyle{ S\subset\mathbb{F} }[/math] be an arbitrary set and [math]\displaystyle{ x\in S }[/math] is chosen uniformly at random from [math]\displaystyle{ S }[/math]. If [math]\displaystyle{ P\not\equiv 0 }[/math] then
- [math]\displaystyle{ \Pr[P(x)=0]\le\frac{d}{|S|}. }[/math]
- Let [math]\displaystyle{ P\in\mathbb{F}[x] }[/math] be a polynomial of degree [math]\displaystyle{ d }[/math] over the field [math]\displaystyle{ \mathbb{F} }[/math]. Let [math]\displaystyle{ S\subset\mathbb{F} }[/math] be an arbitrary set and [math]\displaystyle{ x\in S }[/math] is chosen uniformly at random from [math]\displaystyle{ S }[/math]. If [math]\displaystyle{ P\not\equiv 0 }[/math] then
Proof. A non-zero [math]\displaystyle{ d }[/math]-degree polynomial [math]\displaystyle{ P }[/math] has at most [math]\displaystyle{ d }[/math] distinct roots, thus at most [math]\displaystyle{ d }[/math] members [math]\displaystyle{ x }[/math] of [math]\displaystyle{ S }[/math] satisfy that [math]\displaystyle{ P(x)=0 }[/math]. Therefore, [math]\displaystyle{ \Pr[P(x)=0]\le\frac{d}{|S|} }[/math].
- [math]\displaystyle{ \square }[/math]
By the theorem, the algorithm can distinguish a non-zero polynomial from 0 with probability at least [math]\displaystyle{ 1/2 }[/math]. This is achieved by evaluation of the polynomial at only one point and [math]\displaystyle{ 1+\log_2 d }[/math] many random bits.
Communication Complexity of Identity
The communication complexity is introduced by Andrew Chi-Chih Yao as a model of computation which involves multiple participants, each with partial information of the input.
Assume that there are two entities, say Alice and Bob. Alice has a private input [math]\displaystyle{ a }[/math] and Bob has a private input [math]\displaystyle{ b }[/math]. Together they want to compute a function [math]\displaystyle{ f(a,b) }[/math] by communicating with each other. The communication follows a predefined communication protocol (the "algorithm" in this model) whose logics depends only on the problem [math]\displaystyle{ f }[/math] but not on the inputs. The complexity of a communication protocol is measured by the number of bits communicated between Alice and Bob in the worst case.
The problem of checking identity is formally defined by the function EQ as follows: [math]\displaystyle{ \mathrm{EQ}:\{0,1\}^n\times\{0,1\}^n\rightarrow\{0,1\} }[/math] and for any [math]\displaystyle{ a,b\in\{0,1\}^n }[/math],
- [math]\displaystyle{ \mathrm{EQ}(a,b)= \begin{cases} 1& \mbox{if } a=b,\\ 0& \mbox{otherwise.} \end{cases} }[/math]
A trivial way to solve EQ is to let Bob send his entire input string [math]\displaystyle{ b }[/math] to Alice and let Alice check whether [math]\displaystyle{ a=b }[/math]. This costs [math]\displaystyle{ n }[/math] bits of communications.
It is known that for deterministic communication protocols, this is the best we can get for computing EQ.
Theorem (Yao 1979) - Any deterministic communication protocol computing EQ on two [math]\displaystyle{ n }[/math]-bit strings costs [math]\displaystyle{ n }[/math] bits of communication in the worst-case.
This theorem is much more nontrivial to prove than it looks, because Alice and Bob are allowed to interact with each other in arbitrary ways. The proof of this theorem in Yao's 1979 paper initiates the field of communication complexity.
If the randomness is allowed, we can solve this problem up to a tolerable probabilistic error with significantly less communications. The inputs [math]\displaystyle{ a,b\in\{0,1\}^{n} }[/math] are two strings [math]\displaystyle{ a=a_0a_1\cdots a_{n-1}, b=b_0b_1\cdots b_{n-1} }[/math] of [math]\displaystyle{ n }[/math] bits. Let [math]\displaystyle{ k=\lceil\log_2 (2n)\rceil }[/math] and [math]\displaystyle{ p\in[2^k,2^{k+1}] }[/math] be an arbitrary prime number. (Such a prime [math]\displaystyle{ p }[/math] always exists.) The input strings [math]\displaystyle{ a,b }[/math] can be respectively represented as two polynomials [math]\displaystyle{ f,g\in\mathbb{Z}_p[x] }[/math] such that [math]\displaystyle{ f(x)=\sum_{i=0}^{n-1}a_ix^{i} }[/math] and [math]\displaystyle{ g(x)=\sum_{i=0}^{n-1}b_ix^{i} }[/math] of degree [math]\displaystyle{ n-1 }[/math], where all additions and multiplications are modulo [math]\displaystyle{ p }[/math]. The randomized communication protocol is given as follows:
A randomized protocol for EQ Alice does:
- pick [math]\displaystyle{ x\in[p] }[/math] uniformly at random;
- send [math]\displaystyle{ x }[/math] and [math]\displaystyle{ f(x) }[/math] to Bob;
Upon receiving [math]\displaystyle{ x }[/math] and [math]\displaystyle{ f(x) }[/math] Bob does:
- If [math]\displaystyle{ f(x)= g(x) }[/math] return "yes"; else return "no".
Repeat this protocol for 100 times. The total number of bits to communicate is bounded by [math]\displaystyle{ 200\log_2p=O(\log n) }[/math]. Due to the analysis of the randomized algorithm for PIT, if [math]\displaystyle{ a=b }[/math] the protocol is always correct and if [math]\displaystyle{ a\neq b }[/math] the protocol fails to report a difference with probability less than [math]\displaystyle{ 2^{-100} }[/math].