随机算法 (Spring 2013)/Mixing Time and Coupling
Mixing Time
The mixing time of a Markov chain gives the rate at which a Markov chain converges to the stationary distribution. To rigorously define this notion, we need a way of measuring the closeness between two distributions.
Total Variation Distance
In probability theory, the total variation distance measures the difference between two probability distributions.
Definition (total variation distance) - Let [math]\displaystyle{ p }[/math] and [math]\displaystyle{ q }[/math] be two probability distributions over the same finite state space [math]\displaystyle{ \Omega }[/math], the total variation distance between [math]\displaystyle{ p }[/math] and [math]\displaystyle{ q }[/math] is defined as
- [math]\displaystyle{ \|p-q\|_{TV}=\frac{1}{2}\sum_{x\in\Omega}|p(x)-q(x)|=\frac{1}{2}\|p-q\|_1 }[/math],
- where [math]\displaystyle{ \|\cdot\|_1 }[/math] is the [math]\displaystyle{ \ell_1 }[/math]-norm of vectors.
- Let [math]\displaystyle{ p }[/math] and [math]\displaystyle{ q }[/math] be two probability distributions over the same finite state space [math]\displaystyle{ \Omega }[/math], the total variation distance between [math]\displaystyle{ p }[/math] and [math]\displaystyle{ q }[/math] is defined as
It can be verified (left as an exercise) that
- [math]\displaystyle{ \max_{A\subset\Omega}|p(A)-q(A)|=\frac{1}{2}\sum_{x\in\Omega}|p(x)-q(x)| }[/math],
thus the total variation distance can be equivalently defined as
- [math]\displaystyle{ \|p-q\|_{TV}=\max_{A\subset\Omega}|p(A)-q(A)| }[/math].
So the total variation distance between two distributions gives an upper bound on the difference between the probabilities of the same event according to the two distributions.
Mixing Time
Definition (mixing time) - Let [math]\displaystyle{ \pi }[/math] be the stationary of the chain, and [math]\displaystyle{ p_x^{(t)} }[/math] be the distribution after [math]\displaystyle{ t }[/math] steps when the initial state is [math]\displaystyle{ x }[/math].
- [math]\displaystyle{ \Delta_x(t)=\|p_x^{(t)}-\pi\|_{TV} }[/math] is the distance to stationary distribution [math]\displaystyle{ \pi }[/math] after [math]\displaystyle{ t }[/math] steps, started at state [math]\displaystyle{ x }[/math].
- [math]\displaystyle{ \Delta(t)=\max_{x\in\Omega}\Delta_x(t) }[/math] is the maximum distance to stationary distribution [math]\displaystyle{ \pi }[/math] after [math]\displaystyle{ t }[/math] steps.
- [math]\displaystyle{ \tau_x(\epsilon)=\min\{t\mid\Delta_x(t)\le\epsilon\} }[/math] is the time until the total variation distance to the stationary distribution, started at the initial state [math]\displaystyle{ x }[/math], reaches [math]\displaystyle{ \epsilon }[/math].
- [math]\displaystyle{ \tau(\epsilon)=\max_{x\in\Omega}\tau_x(\epsilon) }[/math] is the time until the total variation distance to the stationary distribution, started at the worst possible initial state, reaches [math]\displaystyle{ \epsilon }[/math].
- Let [math]\displaystyle{ \pi }[/math] be the stationary of the chain, and [math]\displaystyle{ p_x^{(t)} }[/math] be the distribution after [math]\displaystyle{ t }[/math] steps when the initial state is [math]\displaystyle{ x }[/math].
We note that [math]\displaystyle{ \Delta_x(t) }[/math] is monotonically non-increasing in [math]\displaystyle{ t }[/math]. So the definition of [math]\displaystyle{ \tau_x(\epsilon) }[/math] makes sense, and is actually the inverse of [math]\displaystyle{ \Delta_x(t) }[/math].
Definition (mixing time) - The mixing time [math]\displaystyle{ \tau_{\mathrm{mix}} }[/math] of a Markov chain is [math]\displaystyle{ \tau(1/2\mathrm{e}) }[/math].
The mixing time is the time until the total variation distance to the stationary distribution, starting from the worst possible initial state [math]\displaystyle{ x\in\Omega }[/math], reaches [math]\displaystyle{ \frac{1}{2\mathrm{e}} }[/math]. The value [math]\displaystyle{ \frac{1}{2\mathrm{e}} }[/math] is chosen just for the convenience of calculation. The next proposition says that [math]\displaystyle{ \tau(\epsilon) }[/math] with general [math]\displaystyle{ \epsilon }[/math] can be estimated from [math]\displaystyle{ \tau_{\mathrm{mix}} }[/math].
Proposition - [math]\displaystyle{ \Delta(k\cdot\tau_{\mathrm{mix}})\le \mathrm{e}^{-k} }[/math] for any integer [math]\displaystyle{ k\ge1 }[/math].
- [math]\displaystyle{ \tau(\epsilon)\le\tau_{\mathrm{mix}}\cdot\left\lceil\ln\frac{1}{\epsilon}\right\rceil }[/math].
So the distance to stationary distribution [math]\displaystyle{ \Delta(t) }[/math] decays exponentially in multiplications of [math]\displaystyle{ \tau_\mathrm{mix} }[/math].
Both the formal proofs of the monotonicity of [math]\displaystyle{ \Delta_x(t) }[/math] and the above proposition uses the coupling technique and is postponed to next section.
Coupling
We will discuss how to bound the mixing time by coupling two Markov chains. Before that, we will first formally introduce the coupling of two probability distributions.
Coupling of Two Distributions
Coupling is a powerful proof technique in probability theory. It allows us to compare two unrelated variables (or processes) by forcing them to share some randomness.
Definition (coupling) - Let [math]\displaystyle{ p }[/math] and [math]\displaystyle{ q }[/math] be two probability distributions over [math]\displaystyle{ \Omega }[/math]. A probability distribution [math]\displaystyle{ \mu }[/math] over [math]\displaystyle{ \Omega\times\Omega }[/math] is said to be a coupling if its marginal distributions are [math]\displaystyle{ p }[/math] and [math]\displaystyle{ q }[/math]; that is
- [math]\displaystyle{ \begin{align} p(x) &=\sum_{y\in\Omega}\mu(x,y);\\ q(x) &=\sum_{y\in\Omega}\mu(y,x). \end{align} }[/math]
- Let [math]\displaystyle{ p }[/math] and [math]\displaystyle{ q }[/math] be two probability distributions over [math]\displaystyle{ \Omega }[/math]. A probability distribution [math]\displaystyle{ \mu }[/math] over [math]\displaystyle{ \Omega\times\Omega }[/math] is said to be a coupling if its marginal distributions are [math]\displaystyle{ p }[/math] and [math]\displaystyle{ q }[/math]; that is
The interesting case is when [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] are not independent. In particular, we want the probability that [math]\displaystyle{ X=Y }[/math] to be as large as possible, yet still maintaining the respective marginal distributions [math]\displaystyle{ p }[/math] and [math]\displaystyle{ q }[/math]. When [math]\displaystyle{ p }[/math] and [math]\displaystyle{ q }[/math] are different it is inevitable that [math]\displaystyle{ X\neq Y }[/math] with some probability, but how small this probability can be, that is, how well two distributions can be coupled? The following coupling lemma states that this is determined by the total variation distance between the two distributions.
Lemma (coupling lemma) - Let [math]\displaystyle{ p }[/math] and [math]\displaystyle{ q }[/math] be two probability distributions over [math]\displaystyle{ \Omega }[/math].
- For any coupling [math]\displaystyle{ (X,Y) }[/math] of [math]\displaystyle{ p }[/math] and [math]\displaystyle{ q }[/math], it holds that [math]\displaystyle{ \Pr[X\neq Y]\ge\|p-q\|_{TV} }[/math].
- There exists a coupling [math]\displaystyle{ (X,Y) }[/math] of [math]\displaystyle{ p }[/math] and [math]\displaystyle{ q }[/math] such that [math]\displaystyle{ \Pr[X\neq Y]=\|p-q\|_{TV} }[/math].
Proof. - 1.
Suppose [math]\displaystyle{ (X,Y) }[/math] follows the distribution [math]\displaystyle{ \mu }[/math] over [math]\displaystyle{ \Omega\times\Omega }[/math]. Due to the definition of coupling,
- [math]\displaystyle{ \begin{align} p(x) =\sum_{y\in\Omega}\mu(x,y) &\quad\text{and } &q(x) =\sum_{y\in\Omega}\mu(y,x). \end{align} }[/math]
Then for any [math]\displaystyle{ z\in\Omega }[/math], [math]\displaystyle{ \mu(z,z)\le\min\{p(z),q(z)\} }[/math], thus
- [math]\displaystyle{ \begin{align} \Pr[X=Y] &= \sum_{z\in\Omega}\mu(z,z) \le\sum_{z\in\Omega}\min\{p(z),q(z)\}. \end{align} }[/math]
Therefore,
- [math]\displaystyle{ \begin{align} \Pr[X\neq Y] &\ge 1-\sum_{z\in\Omega}\min\{p(z),q(z)\}\\ &=\sum_{z\in\Omega}(p(z)-\min\{p(z),q(z)\})\\ &=\sum_{z\in\Omega\atop p(z)\gt q(z)}(p(z)-q(z))\\ &=\frac{1}{2}\sum_{z\in\Omega}|p(z)-q(z)|\\ &=\|p-q\|_{TV}. \end{align} }[/math]
- 2.
We can couple [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] so that for each [math]\displaystyle{ z\in\Omega }[/math], [math]\displaystyle{ X=Y=z }[/math] with probability [math]\displaystyle{ \min\{p(z),q(z)\} }[/math]. The remaining follows as above.
- [math]\displaystyle{ \square }[/math]
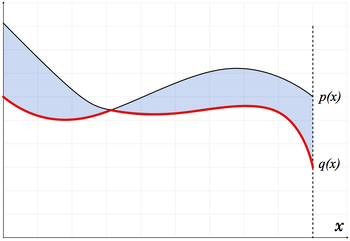
The proof is depicted by the following figure, where the curves are the probability density functions for the two distributions [math]\displaystyle{ p }[/math] and [math]\displaystyle{ q }[/math], the colored area is the diference between the two distribution, and the "lower envelope" (the red line) is the [math]\displaystyle{ \min\{p(x), q(x)\} }[/math].
Monotonicity of [math]\displaystyle{ \Delta_x(t) }[/math]
Consider a Markov chain on state space [math]\displaystyle{ \Omega }[/math]. Let [math]\displaystyle{ \pi }[/math] be the stationary distribution, and [math]\displaystyle{ p_x^{(t)} }[/math] be the distribution after [math]\displaystyle{ t }[/math] steps when the initial state is [math]\displaystyle{ x }[/math]. Recall that [math]\displaystyle{ \Delta_x(t)=\|p_x^{(t)}-\pi\|_{TV} }[/math] is the distance to stationary distribution [math]\displaystyle{ \pi }[/math] after [math]\displaystyle{ t }[/math] steps, started at state [math]\displaystyle{ x }[/math].
We will show that [math]\displaystyle{ \Delta_x(t) }[/math] is non-decreasing in [math]\displaystyle{ t }[/math]. That is, for a Markov chain, the variation distance to the stationary distribution monotonically decreases as time passes. Although this is rather intuitive at the first glance, the proof is nontrivial. A brute force (algebraic) proof can be obtained by analyze the change to the 1-norm of [math]\displaystyle{ p_x^{(t)}-\pi }[/math] by multiplying the transition matrix [math]\displaystyle{ P }[/math]. The analysis uses eigen decomposition. We introduce a cleverer proof using coupling.
Proposition - [math]\displaystyle{ \Delta_x(t) }[/math] is non-decreasing in [math]\displaystyle{ t }[/math].
Proof. Let [math]\displaystyle{ X_0=x }[/math] and [math]\displaystyle{ Y_0 }[/math] follow the stationary distribution [math]\displaystyle{ \pi }[/math]. Two chains [math]\displaystyle{ X_0,X_1,X_2,\ldots }[/math] and [math]\displaystyle{ Y_0,Y_1,Y_2,\ldots }[/math] can be defined by the initial distributions [math]\displaystyle{ X_0 }[/math] and [math]\displaystyle{ Y_0 }[/math]. The distributions of [math]\displaystyle{ X_t }[/math] and [math]\displaystyle{ Y_t }[/math] are [math]\displaystyle{ p_x^{(t)} }[/math] and [math]\displaystyle{ \pi }[/math], respectively.
For any fixed [math]\displaystyle{ t }[/math], we can couple [math]\displaystyle{ X_t }[/math] and [math]\displaystyle{ Y_t }[/math] such that [math]\displaystyle{ \Pr[X_t\neq Y_t]=\|p_x^{(t)}-\pi\|_{TV}=\Delta_x(t) }[/math]. Due to the Coupling Lemma, such coupling exists. We then define a coupling between [math]\displaystyle{ X_{t+1} }[/math] and [math]\displaystyle{ Y_{t+1} }[/math] as follows.
- If [math]\displaystyle{ X_t=Y_t }[/math], then [math]\displaystyle{ X_{t+1}=Y_{t+1} }[/math] following the transition matrix of the Markov chain.
- Otherwise, do the transitions [math]\displaystyle{ X_t\rightarrow X_{t+1} }[/math] and [math]\displaystyle{ Y_t\rightarrow Y_{t+1} }[/math] independently, following the transitin matrix.
It is easy to see that the marginal distributions of [math]\displaystyle{ X_{t+1} }[/math] and [math]\displaystyle{ Y_{t+1} }[/math] both follow the original Markov chain, and
- [math]\displaystyle{ \Pr[X_{t+1}\neq Y_{t+1}]\le \Pr[X_t\neq Y_{t}]. }[/math]
In conclusion, it holds that
- [math]\displaystyle{ \Delta_x(t+1)=\|p_x^{(t+1)}-\pi\|_{TV}\le\Pr[X_{t+1}\neq Y_{t+1}]\le \Pr[X_t\neq Y_{t}]=\Delta_x(t), }[/math]
where the first inequality is due to the easy direction of the Coupling Lemma.
- [math]\displaystyle{ \square }[/math]
Rapid Mixing by Coupling
Consider an ergodic (irreducible and aperiodic) Markov chain on finite state space [math]\displaystyle{ \Omega }[/math]. We want to upper bound its mixing time. The coupling technique for bounding the mixing time can be sumerized as follows:
- Consider two random walks starting at state [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] in [math]\displaystyle{ \Omega }[/math]. Each individual walk follows the transition rule of the original Markov chain. But the two random walks may be "coupled" in some way, that is, may be correlated with each other. A key observation is that for any such coupling, it always holds that
- [math]\displaystyle{ \Delta(t) \le\max_{x,y\in\Omega}\Pr[\text{ the two } \mathit{coupled} \text{ random walks started at }x,y\text{ have not met by time }t] }[/math]
- where we recall that [math]\displaystyle{ \Delta(t)=\max_{x\in\Omega}\|p_x^{(t)}-\pi\|_{TV} }[/math].
Definition (coupling of Markov chain) - A coupling of a Markov chain with state space [math]\displaystyle{ \Omega }[/math] and transition matrix [math]\displaystyle{ P }[/math], is a Markov chain [math]\displaystyle{ (X_t,Y_t) }[/math] with state space [math]\displaystyle{ \Omega\times\Omega }[/math], satisfying
- each of [math]\displaystyle{ X_t }[/math] and [math]\displaystyle{ Y_t }[/math] viewed in isolation is a faithful copy of the original Markov chain, i.e.
- [math]\displaystyle{ \Pr[X_{t+1}=v\mid X_t=u]=\Pr[Y_{t+1}=v\mid Y_{t}=u]=P(u,v) }[/math];
- once [math]\displaystyle{ X_t }[/math] and [math]\displaystyle{ Y_t }[/math] reaches the same state, they make identical moves ever since, i.e.
- [math]\displaystyle{ X_{t+1}=Y_{t+1} }[/math] if [math]\displaystyle{ X_t=Y_t }[/math].
Lemma (coupling lemma for Markov chains) - Let [math]\displaystyle{ (X_t,Y_t) }[/math] be a coupling of a Markov chain [math]\displaystyle{ M }[/math] with state space [math]\displaystyle{ \Omega }[/math]. Then [math]\displaystyle{ \Delta(t) }[/math] for [math]\displaystyle{ M }[/math] is bounded by
- [math]\displaystyle{ \Delta(t) \le\max_{x,y\in\Omega}\Pr[X_t\neq Y_t\mid X_0=x,Y_0=y] }[/math].
- Let [math]\displaystyle{ (X_t,Y_t) }[/math] be a coupling of a Markov chain [math]\displaystyle{ M }[/math] with state space [math]\displaystyle{ \Omega }[/math]. Then [math]\displaystyle{ \Delta(t) }[/math] for [math]\displaystyle{ M }[/math] is bounded by
Proof. Due to the coupling lemma (for probability distributions),
- [math]\displaystyle{ \Pr[X_t\neq Y_t\mid X_0=x,Y_0=y] \ge \|p_x^{(t)}-p_y^{(t)}\|_{TV}, }[/math]
where [math]\displaystyle{ p_x^{(t)},p_y^{(t)} }[/math] are distributions of the Markov chain [math]\displaystyle{ M }[/math] at time [math]\displaystyle{ t }[/math], started at states [math]\displaystyle{ x, y }[/math].
Therefore,
- [math]\displaystyle{ \begin{align} \Delta(t) &= \max_{x\in\Omega}\|p_x^{(t)}-\pi\|_{TV}\\ &\le \max_{x,y\in\Omega}\|p_x^{(t)}-p_y^{(t)}\|_{TV}\\ &\le \max_{x,y\in\Omega}\Pr[X_t\neq Y_t\mid X_0=x,Y_0=y]. \end{align} }[/math]
- [math]\displaystyle{ \square }[/math]
Corollary - Let [math]\displaystyle{ (X_t,Y_t) }[/math] be a coupling of a Markov chain [math]\displaystyle{ M }[/math] with state space [math]\displaystyle{ \Omega }[/math]. Then [math]\displaystyle{ \tau(\epsilon) }[/math] for [math]\displaystyle{ M }[/math] is bounded as follows:
- [math]\displaystyle{ \max_{x,y\in\Omega}\Pr[X_t\neq Y_t\mid X_0=x,Y_0=y]\le \epsilon\quad\Longrightarrow\quad\tau(\epsilon)\le t }[/math].
- Let [math]\displaystyle{ (X_t,Y_t) }[/math] be a coupling of a Markov chain [math]\displaystyle{ M }[/math] with state space [math]\displaystyle{ \Omega }[/math]. Then [math]\displaystyle{ \tau(\epsilon) }[/math] for [math]\displaystyle{ M }[/math] is bounded as follows:
Geometric convergence
Consider a Markov chain on state space [math]\displaystyle{ \Omega }[/math]. Let [math]\displaystyle{ \pi }[/math] be the stationary distribution, and [math]\displaystyle{ p_x^{(t)} }[/math] be the distribution after [math]\displaystyle{ t }[/math] steps when the initial state is [math]\displaystyle{ x }[/math]. Recall that
- [math]\displaystyle{ \Delta_x(t)=\|p_x^{(t)}-\pi\|_{TV} }[/math];
- [math]\displaystyle{ \Delta(t)=\max_{x\in\Omega}\Delta_x(t) }[/math];
- [math]\displaystyle{ \tau_x(\epsilon)=\min\{t\mid\Delta_x(t)\le\epsilon\} }[/math];
- [math]\displaystyle{ \tau(\epsilon)=\max_{x\in\Omega}\tau_x(\epsilon) }[/math];
- [math]\displaystyle{ \tau_{\mathrm{mix}}=\tau(1/2\mathrm{e})\, }[/math].
We prove that
Proposition - [math]\displaystyle{ \Delta(k\cdot\tau_{\mathrm{mix}})\le \mathrm{e}^{-k} }[/math] for any integer [math]\displaystyle{ k\ge1 }[/math].
- [math]\displaystyle{ \tau(\epsilon)\le\tau_{\mathrm{mix}}\cdot\left\lceil\ln\frac{1}{\epsilon}\right\rceil }[/math].
Proof. - 1.
We denote that [math]\displaystyle{ \tau=\tau_{\mathrm{mix}}\, }[/math]. We construct a coupling of the Markov chain as follows. Suppose [math]\displaystyle{ t=k\tau }[/math] for some integer [math]\displaystyle{ k }[/math].
- If [math]\displaystyle{ X_t=Y_t }[/math] then [math]\displaystyle{ X_{t+i}=Y_{t+i} }[/math] for [math]\displaystyle{ i=1,2,\ldots,\tau }[/math].
- For the case that [math]\displaystyle{ X_t=u, Y_t=v }[/math] for some [math]\displaystyle{ u\neq v }[/math], we couple the [math]\displaystyle{ X_{t+\tau} }[/math] and [math]\displaystyle{ Y_{t+\tau} }[/math] so that [math]\displaystyle{ \Pr[X_{t+\tau}\neq Y_{t+\tau}\mid X_t=u,Y_t=v]=\|p_u^{(t)}-p_v^{(t)}\|_{TV} }[/math]. Due to the Coupling Lemma, such coupling does exist.
For any [math]\displaystyle{ u,v\in\Omega }[/math] that [math]\displaystyle{ u\neq v }[/math],
- [math]\displaystyle{ \begin{align} \Pr[X_{t+\tau}\neq Y_{t+\tau}\mid X_t=u,Y_t=v] &=\|p_u^{(\tau)}-p_v^{(\tau)}\|_{TV}\\ &\le \|p_u^{(\tau)}-\pi\|_{TV}+\|p_v^{(\tau)}-\pi\|_{TV}\\ &= \Delta_u(\tau)+\Delta_v(\tau)\\ &\le \frac{1}{\mathrm{e}}. \end{align} }[/math]
Thus [math]\displaystyle{ \Pr[X_{t+\tau}\neq Y_{t+\tau}\mid X_t\neq Y_t]\le \frac{1}{\mathrm{e}} }[/math] by the law of total probability. Therefore, for any [math]\displaystyle{ x,y\in\Omega }[/math],
- [math]\displaystyle{ \begin{align} &\quad\, \Pr[X_{t+\tau}\neq Y_{t+\tau}\mid X_0=x,Y_0=y]\\ &= \Pr[X_{t+\tau}\neq Y_{t+\tau}\mid X_t\neq Y_t]\cdot \Pr[X_{t}\neq Y_{t}\mid X_0=x,Y_0=y]\\ &\le \frac{1}{\mathrm{e}}\Pr[X_{t}\neq Y_{t}\mid X_0=x,Y_0=y]. \end{align} }[/math]
Then by induction,
- [math]\displaystyle{ \Pr[X_{k\tau}\neq Y_{k\tau}\mid X_0=x,Y_0=y]\le \mathrm{e}^{-k}, }[/math]
and this holds for any [math]\displaystyle{ x,y\in\Omega }[/math]. By the Coupling Lemma for Markov chains, this means [math]\displaystyle{ \Delta(k\tau_{\mathrm{mix}})=\Delta(k\tau)\le\mathrm{e}^{-k} }[/math].
- 2.
By the definition of [math]\displaystyle{ \tau(\epsilon) }[/math], the inequality is straightforwardly implied by (1).
- [math]\displaystyle{ \square }[/math]
Application: Random Walk on the Hypercube
A [math]\displaystyle{ n }[/math]-dimensional hypercube is a graph on vertex set [math]\displaystyle{ \{0,1\}^n }[/math]. For any [math]\displaystyle{ x,y\in\{0,1\}^n }[/math], there is an edge between [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] if [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] differ at exact one coordinate (the hamming distance between [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] is 1).
We use coupling to bound the mixing time of the following simple random walk on a hypercube.
Random Walk on Hypercube - At each step, for the current state [math]\displaystyle{ x\in\{0,1\}^n }[/math]:
- with probability [math]\displaystyle{ 1/2 }[/math], do nothing;
- else, pick a coordinate [math]\displaystyle{ i\in\{1,2,\ldots,n\} }[/math] uniformly at random and flip the bit [math]\displaystyle{ x_i }[/math] (change [math]\displaystyle{ x_i }[/math] to [math]\displaystyle{ 1-x_i }[/math]).
This is a lazy uniform random walk in an [math]\displaystyle{ n }[/math]-dimensional hypercube. It is equivalent to the following random walk.
Random Walk on Hypercube - At each step, for the current state [math]\displaystyle{ x\in\{0,1\}^n }[/math]:
- pick a coordinate [math]\displaystyle{ i\in\{1,2,\ldots,n\} }[/math] uniformly at random and a bit [math]\displaystyle{ b\in\{0,1\} }[/math] uniformly at random;
- let [math]\displaystyle{ x_i=b }[/math].
It is easy to see the two random walks are the same. The second form hint us to couple the random choice of [math]\displaystyle{ i }[/math] and [math]\displaystyle{ b }[/math] in each step. Consider two copies of the random walk [math]\displaystyle{ X_t }[/math] and [math]\displaystyle{ Y_t }[/math], started from arbitrary two states [math]\displaystyle{ X_0 }[/math] and [math]\displaystyle{ Y_0 }[/math], the coupling rule is:
- At each step, [math]\displaystyle{ X_t }[/math] and [math]\displaystyle{ Y_t }[/math] choose the same (uniformly random) coordinate [math]\displaystyle{ i }[/math] and the same (uniformly random) bit [math]\displaystyle{ b }[/math].
Obviously the two individual random walks are both faithful copies of the original walk.
For arbitrary [math]\displaystyle{ x,y\in\{0,1\}^n }[/math], started at [math]\displaystyle{ X_0=x, Y_0=y }[/math], the event [math]\displaystyle{ X_t=Y_t }[/math] occurs if everyone of the coordinates on which [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] disagree has been picked at least once. In the worst case, [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] disagree on all [math]\displaystyle{ n }[/math] coordinates. The time [math]\displaystyle{ T }[/math] that all [math]\displaystyle{ n }[/math] coordinates have been picked follows the coupon collector problem collecting [math]\displaystyle{ n }[/math] coupons, and we know from the coupon collector problem that for [math]\displaystyle{ c\gt 0 }[/math],
- [math]\displaystyle{ \Pr[T\ge n\ln n+cn]\le \mathrm{e}^{-c}. }[/math]
Thus for any [math]\displaystyle{ x,y\in\{0,1\}^n }[/math], if [math]\displaystyle{ t\ge n\ln n+cn }[/math], then [math]\displaystyle{ \Pr[X_t\neq Y_t\mid X_0=x,Y_0=y]\le \mathrm{e}^{-c} }[/math]. Due to the coupling lemma for Markov chains,
- [math]\displaystyle{ \Delta(n\ln n+cn)\le \mathrm{e}^{-c}, }[/math]
which implies that
- [math]\displaystyle{ \tau(\epsilon)=n\ln n+n\ln\frac{1}{\epsilon} }[/math].
So the random walk achieves a polynomially small variation distance [math]\displaystyle{ \epsilon=\frac{1}{\mathrm{poly}(n)} }[/math] to the stationary distribution in time [math]\displaystyle{ O(n\ln n) }[/math].
Note that the number of states (vertices in the [math]\displaystyle{ n }[/math]-dimensional hypercube) is [math]\displaystyle{ 2^n }[/math]. Therefore, the mixing time is exponentially small compared to the size of the state space.
Card Shuffling
We consider the Markov chain of shuffling a deck of cards, and prove the rapid mixing of the chain by coupling.
Riffle Shuffle
The following is the Gilbert-Shannon-Reeds model of riffle shuffle introduced by Gilbert and Shannon in 1955 and independently by Reeds in 1985.
Riffle Shuffle (Gilbert-Shannon 1955; Reeds 1985) - Given a deck of [math]\displaystyle{ n }[/math] cards, at each round, do as follows.
- Split the original deck into two decks according to the binomial distribution [math]\displaystyle{ \mathrm{Bin}(n,1/2) }[/math].
- Cut off the first [math]\displaystyle{ k }[/math] cards with probability [math]\displaystyle{ \frac{{n\choose k}}{2^n} }[/math], put into the left deck, and put the rest [math]\displaystyle{ n-k }[/math] cards into the right deck.
- Drop cards in sequence, where the next card comes from one of the two decks with probability proportional to the size of the deck at that time.
- Suppose at a step there are [math]\displaystyle{ L }[/math] cards in the left deck and [math]\displaystyle{ R }[/math] cards in the right deck. A card is dropped from left with probability [math]\displaystyle{ \frac{L}{L+R} }[/math], and from right otherwise.
The second step actually samples a uniform interleaving of left and right deck. The magician and mathematician Diaconis in 1988 found evidence showing that this mathematical model reasonably approximate the riffle shuffling acted by human.
The above model is equivalent to the following model of inverse riffle shuffle.
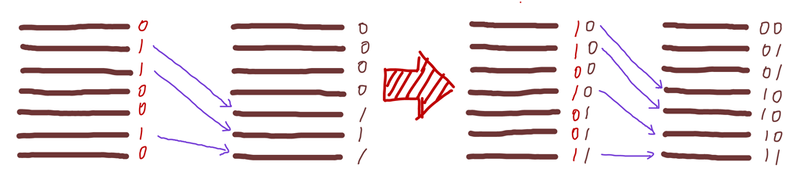
Inverse Riffle Shuffle - Label each card with a bit from [math]\displaystyle{ \{0,1\} }[/math] uniformly and independently at random.
- Place all cards labeled with 0 above all cards labeled with 1, keeping the cards with the same label in the same the relative order as before.
The process of inverse riffle shuffle is depicted as follows.
For each card, the random bits used for labeling the card compose a binary code [math]\displaystyle{ x }[/math], with the [math]\displaystyle{ t }[/math]-th bit (from lower to higher radix) [math]\displaystyle{ x_t }[/math] being the random bit chosen in round [math]\displaystyle{ t }[/math] to label the card.
Lemma - After every round of the inverse riffle shuffle, the cards are sorted in non-decreasing order of their corresponding binary codes.
Proof. By induction. After the first round, all [math]\displaystyle{ 0 }[/math] are above all [math]\displaystyle{ 1 }[/math]s. Assume that the hypothesis is true for the first [math]\displaystyle{ t-1 }[/math] rounds. After the [math]\displaystyle{ t }[/math]-th round, all cards with the highest coordinate [math]\displaystyle{ x_t=0 }[/math] are above all cards with [math]\displaystyle{ x_t=1 }[/math], and by the definition of inverse riffle shuffle, cards with the same highest bit [math]\displaystyle{ x_t }[/math] are kept in the same relative order as they are after the [math]\displaystyle{ (t-1) }[/math]-th round of the shuffling, which due to the hypothesis, means that the cards with the same highest bit [math]\displaystyle{ x_t }[/math] are sorted in the non-decreasing order of [math]\displaystyle{ x_{t-1}x_{t-2}\cdots x_1 }[/math]. By the definition of binary representation, all cards are sorted.
- [math]\displaystyle{ \square }[/math]
Rapid Mixing of Riffle Shuffle by Coupling
Theorem - The mixing time of inverse riffle shuffle of a deck of [math]\displaystyle{ n }[/math] cards is [math]\displaystyle{ \tau_{\mathrm{mix}}=O(\log n) }[/math].
Consider two instance of shuffling, started with two decks, each in an arbitrary order. We couple the two shuffling processes by coupling their random choices of labelings:
- In each round, we label the same cards (same content, not the same order) in the two decks with the same random bit.
Formally, for each [math]\displaystyle{ i\in[n] }[/math], we uniformly and independently choose a random [math]\displaystyle{ b_i\in\{0,1\} }[/math] as the label of the card [math]\displaystyle{ i }[/math] in each of the two decks in that round. It is easy to see that, each of the two shuffling processes viewed individually follows exactly the rules of inverse riffle shuffle.
Lemma - With the above coupling rule, started with arbitrary two decks of cards, the two decks are the same once all cards in the first (or the second) deck have distinct labels.
Proof. By the definition of the coupling rule, any two identical cards in the two decks always have the same label, since in every round they choose the same random bit. And we have shown that after each round, the labels are sorted in non-decreasing order. Thus, we can conclude:
- after each round, the sequences of the labels of the two decks are identical (and sorted in non-decreasing order).
Therefore, when all cards in the first deck have distinct labels, the second deck have the same set of distinct labels, and the cards are sorted increasingly in their labels in the respective decks. Since any two identical cards have the same labels, the cards in the two decks must be in the same order.
- [math]\displaystyle{ \square }[/math]
We denote by [math]\displaystyle{ T }[/math] the random variable representing the time that in an inverse riffle shuffle, all cards in the deck have distinct labels. Due to the coupling lemma for Markov chains,
- [math]\displaystyle{ \Delta(t)\le\Pr[T\ge t] }[/math].
This bound can be deduced from the birthday problem. After [math]\displaystyle{ t }[/math] round, each of the [math]\displaystyle{ n }[/math] cards is randomly assigned one of the [math]\displaystyle{ 2^t }[/math] possible labels. We know that for some [math]\displaystyle{ 2^t=O(n^2) }[/math], i.e. [math]\displaystyle{ t=2\log n+O(1) }[/math], the probability that no two cards have the same label is [math]\displaystyle{ \gt 1-1/2\mathrm{e} }[/math], i.e. [math]\displaystyle{ \Delta(t)\lt 1/2\mathrm{e} }[/math], thus
- [math]\displaystyle{ \tau_{\mathrm{mix}}\le 2\log n+O(1) }[/math].
Note that the state space is the set of all permutations, which is of size [math]\displaystyle{ n! }[/math], whose logarithm is still as large as [math]\displaystyle{ \log (n!)=O(n\ln n) }[/math] due to Stirling's approximation. Thus the riffle shuffle is mixing extremely fast.
This estimation of mixing time is fairly tight. For the case that [math]\displaystyle{ n=52 }[/math], the real mixing rate is as follows.
[math]\displaystyle{ t }[/math] 1 2 3 4 5 6 7 8 9 [math]\displaystyle{ \Delta(t) }[/math] 1.000 1.000 1.000 1.000 0.924 0.614 0.334 0.167 0.003
Graph Colorings
A proper coloring of a graph [math]\displaystyle{ G(V,E) }[/math] is a mapping [math]\displaystyle{ f:V\rightarrow[q] }[/math] for some integer [math]\displaystyle{ q }[/math], satisfying that [math]\displaystyle{ f(u)\neq f(v) }[/math] for all [math]\displaystyle{ uv\in E }[/math].
We consider the problem of sampling a uniformly random proper coloring of a given graph. We will later see that this is useful for counting the number of proper colorings of a given graph, which is a fundamental combinatorial problem, having important applications in statistic physics.
Let's first consider the decision version of the problem. That is, given as input a graph [math]\displaystyle{ G(V,E) }[/math], decide whether there exists a proper [math]\displaystyle{ q }[/math]-coloring of [math]\displaystyle{ G }[/math]. Denote by [math]\displaystyle{ \Delta }[/math] the maximum degree of [math]\displaystyle{ G }[/math].
- If [math]\displaystyle{ q\ge \Delta+1 }[/math], there always exists a proper coloring. Moreover, the proper coloring can be found by a simple greedy algorithm.
- If [math]\displaystyle{ q=\Delta }[/math], [math]\displaystyle{ G }[/math] has a proper coloring unless it contains a [math]\displaystyle{ (\Delta+1) }[/math]-clique or it is an odd cycle. (Brooks Theorem)
- If [math]\displaystyle{ q\lt \Delta }[/math], the problem is NP-hard.
Sampling a random coloring is at least as hard as deciding its existence, so we don't expect to solve the sampling problem when [math]\displaystyle{ q\lt \Delta }[/math]. The decision problem for the case [math]\displaystyle{ q=\Delta }[/math] is also nontrivial. Thus people are interested only in the case when [math]\displaystyle{ q\ge \Delta+1 }[/math].
The following is a natural Markov chain for sampling proper colorings.
Markov Chain for Graph Coloring [math]\displaystyle{ \mathcal{M}_c }[/math] - Start with a proper coloring of [math]\displaystyle{ G(V,E) }[/math]. At each step:
- Pick a vertex [math]\displaystyle{ v\in V }[/math] and a color [math]\displaystyle{ c\in[q] }[/math] uniformly at random.
- Change the color of [math]\displaystyle{ v }[/math] to [math]\displaystyle{ c }[/math] if the resulting coloring is proper; do nothing if otherwise.
For a fixed graph [math]\displaystyle{ G(V,E) }[/math], the state space of the above Markov chain is the set of all proper colorings of [math]\displaystyle{ G }[/math] with [math]\displaystyle{ q }[/math] colors.
Lemma The followings hold for [math]\displaystyle{ \mathcal{M}_c }[/math].
- Aperiodic.
- The transition matrix is symmetric.
- Irreducible if [math]\displaystyle{ q\ge \Delta+2 }[/math].
The followings are the two most important conjectures regarding the problem.
Conjecture - [math]\displaystyle{ \mathcal{M}_c }[/math] has mixing time [math]\displaystyle{ O(n\ln n) }[/math] whenever [math]\displaystyle{ q\ge\Delta+2 }[/math].
- Random sampling of proper graph colorings can be done in polynomial time whenever [math]\displaystyle{ q\ge\Delta+1 }[/math].
These two conjectures are still open. People approach them by relax the requirement for the number of colors [math]\displaystyle{ q }[/math]. Intuitively, the larger the [math]\displaystyle{ q }[/math] is, the more freedom we have, the less dependency are there between non-adjacent vertices.
Rapid mixing of the case [math]\displaystyle{ q\gt 4\Delta }[/math]
We couple the two copies of [math]\displaystyle{ \mathcal{M}_c }[/math], [math]\displaystyle{ X_t }[/math] and [math]\displaystyle{ Y_t }[/math], by the following coupling rule:
- At each step, let [math]\displaystyle{ X_t }[/math] and [math]\displaystyle{ Y_t }[/math] choose the same vertex [math]\displaystyle{ v }[/math] and same color [math]\displaystyle{ c }[/math].
Note that by this coupling, it is possible that [math]\displaystyle{ v }[/math] is recolored to [math]\displaystyle{ c }[/math] in both chains, in one of the two chains, or in no chain. We may separate these cases by looking at the Hamming distance between two colorings.
Let [math]\displaystyle{ d(X_t,Y_t) }[/math] be the number of vertices whose colors in [math]\displaystyle{ X_t }[/math] and [math]\displaystyle{ Y_t }[/math] disagree. For each step, for any choice of vertex [math]\displaystyle{ v }[/math] and color [math]\displaystyle{ c }[/math], there are three possible cases:
- "Good move" ([math]\displaystyle{ d(X_t,Y_t) }[/math] decreases by 1): [math]\displaystyle{ X_t }[/math] disagree with [math]\displaystyle{ Y_t }[/math] at [math]\displaystyle{ v }[/math], and [math]\displaystyle{ c }[/math] is not used in the colors of [math]\displaystyle{ v }[/math] in both [math]\displaystyle{ X_t }[/math] and [math]\displaystyle{ Y_t }[/math].
- "Bad move" ([math]\displaystyle{ d(X_t,Y_t) }[/math] increases by 1):
- "Neutral move" ([math]\displaystyle{ d(X_t,Y_t) }[/math] is unchanged):