组合数学 (Fall 2015)/Problem Set 3 and 随机算法 (Fall 2015)/Chernoff Bound: Difference between pages
imported>Etone No edit summary |
imported>Etone |
||
| Line 1: | Line 1: | ||
== | =The Chernoff Bound= | ||
Suppose that we have a fair coin. If we toss it once, then the outcome is completely unpredictable. But if we toss it, say for 1000 times, then the number of HEADs is very likely to be around 500. This striking phenomenon, illustrated in the right figure, is called the '''concentration'''. The Chernoff bound captures the concentration of independent trials. | |||
[[File:Coinflip.png|border|450px|right]] | |||
The Chernoff bound is also a tail bound for the sum of independent random variables which may give us ''exponentially'' sharp bounds. | |||
Before proving the Chernoff bound, we should talk about the moment generating functions. | |||
== Moment generating functions == | |||
The more we know about the moments of a random variable <math>X</math>, the more information we would have about <math>X</math>. There is a so-called '''moment generating function''', which "packs" all the information about the moments of <math>X</math> into one function. | |||
{{Theorem | |||
|Definition| | |||
:The moment generating function of a random variable <math>X</math> is defined as <math>\mathbf{E}\left[\mathrm{e}^{\lambda X}\right]</math> where <math>\lambda</math> is the parameter of the function. | |||
}} | |||
By Taylor's expansion and the linearity of expectations, | |||
:<math>\begin{align} | |||
\mathbf{E}\left[\mathrm{e}^{\lambda X}\right] | |||
&= | |||
\mathbf{E}\left[\sum_{k=0}^\infty\frac{\lambda^k}{k!}X^k\right]\\ | |||
&=\sum_{k=0}^\infty\frac{\lambda^k}{k!}\mathbf{E}\left[X^k\right] | |||
\end{align}</math> | |||
The moment generating function <math>\mathbf{E}\left[\mathrm{e}^{\lambda X}\right]</math> is a function of <math>\lambda</math>. | |||
== The Chernoff bound == | |||
The Chernoff bounds are exponentially sharp tail inequalities for the sum of independent trials. | |||
The bounds are obtained by applying Markov's inequality to the moment generating function of the sum of independent trials, with some appropriate choice of the parameter <math>\lambda</math>. | |||
{{Theorem | |||
|Chernoff bound (the upper tail)| | |||
:Let <math>X=\sum_{i=1}^n X_i</math>, where <math>X_1, X_2, \ldots, X_n</math> are independent Poisson trials. Let <math>\mu=\mathbf{E}[X]</math>. | |||
:Then for any <math>\delta>0</math>, | |||
::<math>\Pr[X\ge (1+\delta)\mu]\le\left(\frac{e^{\delta}}{(1+\delta)^{(1+\delta)}}\right)^{\mu}.</math> | |||
}} | |||
{{Proof| For any <math>\lambda>0</math>, <math>X\ge (1+\delta)\mu</math> is equivalent to that <math>e^{\lambda X}\ge e^{\lambda (1+\delta)\mu}</math>, thus | |||
:<math>\begin{align} | |||
\Pr[X\ge (1+\delta)\mu] | |||
&= | |||
\Pr\left[e^{\lambda X}\ge e^{\lambda (1+\delta)\mu}\right]\\ | |||
&\le | |||
\frac{\mathbf{E}\left[e^{\lambda X}\right]}{e^{\lambda (1+\delta)\mu}}, | |||
\end{align}</math> | |||
where the last step follows by Markov's inequality. | |||
Computing the moment generating function <math>\mathbf{E}[e^{\lambda X}]</math>: | |||
:<math>\begin{align} | |||
\mathbf{E}\left[e^{\lambda X}\right] | |||
&= | |||
\mathbf{E}\left[e^{\lambda \sum_{i=1}^n X_i}\right]\\ | |||
&= | |||
\mathbf{E}\left[\prod_{i=1}^n e^{\lambda X_i}\right]\\ | |||
&= | |||
\prod_{i=1}^n \mathbf{E}\left[e^{\lambda X_i}\right]. | |||
& (\mbox{for independent random variables}) | |||
\end{align}</math> | |||
Let <math>p_i=\Pr[X_i=1]</math> for <math>i=1,2,\ldots,n</math>. Then, | |||
:<math>\mu=\mathbf{E}[X]=\mathbf{E}\left[\sum_{i=1}^n X_i\right]=\sum_{i=1}^n\mathbf{E}[X_i]=\sum_{i=1}^n p_i</math>. | |||
== | We bound the moment generating function for each individual <math>X_i</math> as follows. | ||
:<math>\begin{align} | |||
\mathbf{E}\left[e^{\lambda X_i}\right] | |||
&= | |||
p_i\cdot e^{\lambda\cdot 1}+(1-p_i)\cdot e^{\lambda\cdot 0}\\ | |||
&= | |||
1+p_i(e^\lambda -1)\\ | |||
&\le | |||
e^{p_i(e^\lambda-1)}, | |||
\end{align}</math> | |||
where in the last step we apply the Taylor's expansion so that <math>e^y\ge 1+y</math> where <math>y=p_i(e^\lambda-1)\ge 0</math>. (By doing this, we can transform the product to the sum of <math>p_i</math>, which is <math>\mu</math>.) | |||
Therefore, | |||
For <math> | :<math>\begin{align} | ||
\mathbf{E}\left[e^{\lambda X}\right] | |||
&= | |||
\prod_{i=1}^n \mathbf{E}\left[e^{\lambda X_i}\right]\\ | |||
&\le | |||
\prod_{i=1}^n e^{p_i(e^\lambda-1)}\\ | |||
&= | |||
\exp\left(\sum_{i=1}^n p_i(e^{\lambda}-1)\right)\\ | |||
&= | |||
e^{(e^\lambda-1)\mu}. | |||
\end{align}</math> | |||
Thus, we have shown that for any <math>\lambda>0</math>, | |||
:<math>\begin{align} | |||
\Pr[X\ge (1+\delta)\mu] | |||
&\le | |||
\frac{\mathbf{E}\left[e^{\lambda X}\right]}{e^{\lambda (1+\delta)\mu}}\\ | |||
&\le | |||
\frac{e^{(e^\lambda-1)\mu}}{e^{\lambda (1+\delta)\mu}}\\ | |||
&= | |||
\left(\frac{e^{(e^\lambda-1)}}{e^{\lambda (1+\delta)}}\right)^\mu | |||
\end{align}</math>. | |||
For any <math>\delta>0</math>, we can let <math>\lambda=\ln(1+\delta)>0</math> to get | |||
:<math>\Pr[X\ge (1+\delta)\mu]\le\left(\frac{e^{\delta}}{(1+\delta)^{(1+\delta)}}\right)^{\mu}.</math> | |||
}} | |||
= | The idea of the proof is actually quite clear: we apply Markov's inequality to <math>e^{\lambda X}</math> and for the rest, we just estimate the moment generating function <math>\mathbf{E}[e^{\lambda X}]</math>. To make the bound as tight as possible, we minimized the <math>\frac{e^{(e^\lambda-1)}}{e^{\lambda (1+\delta)}}</math> by setting <math>\lambda=\ln(1+\delta)</math>, which can be justified by taking derivatives of <math>\frac{e^{(e^\lambda-1)}}{e^{\lambda (1+\delta)}}</math>. | ||
( | |||
---- | |||
We then proceed to the lower tail, the probability that the random variable deviates below the mean value: | |||
{{Theorem | |||
|Chernoff bound (the lower tail)| | |||
:Let <math>X=\sum_{i=1}^n X_i</math>, where <math>X_1, X_2, \ldots, X_n</math> are independent Poisson trials. Let <math>\mu=\mathbf{E}[X]</math>. | |||
:Then for any <math>0<\delta<1</math>, | |||
::<math>\Pr[X\le (1-\delta)\mu]\le\left(\frac{e^{-\delta}}{(1-\delta)^{(1-\delta)}}\right)^{\mu}.</math> | |||
}} | |||
{{Proof| For any <math>\lambda<0</math>, by the same analysis as in the upper tail version, | |||
:<math>\begin{align} | |||
\Pr[X\le (1-\delta)\mu] | |||
&= | |||
\Pr\left[e^{\lambda X}\ge e^{\lambda (1-\delta)\mu}\right]\\ | |||
&\le | |||
\frac{\mathbf{E}\left[e^{\lambda X}\right]}{e^{\lambda (1-\delta)\mu}}\\ | |||
&\le | |||
\left(\frac{e^{(e^\lambda-1)}}{e^{\lambda (1-\delta)}}\right)^\mu. | |||
\end{align}</math> | |||
For any <math>0<\delta<1</math>, we can let <math>\lambda=\ln(1-\delta)<0</math> to get | |||
:<math>\Pr[X\ge (1-\delta)\mu]\le\left(\frac{e^{-\delta}}{(1-\delta)^{(1-\delta)}}\right)^{\mu}.</math> | |||
}} | |||
---- | |||
Some useful special forms of the bounds can be derived directly from the above general forms of the bounds. We now know better why we say that the bounds are exponentially sharp. | |||
{{Theorem | |||
|Useful forms of the Chernoff bound| | |||
:Let <math>X=\sum_{i=1}^n X_i</math>, where <math>X_1, X_2, \ldots, X_n</math> are independent Poisson trials. Let <math>\mu=\mathbf{E}[X]</math>. Then | |||
:1. for <math>0<\delta\le 1</math>, | |||
::<math>\Pr[X\ge (1+\delta)\mu]<\exp\left(-\frac{\mu\delta^2}{3}\right);</math> | |||
::<math>\Pr[X\le (1-\delta)\mu]<\exp\left(-\frac{\mu\delta^2}{2}\right);</math> | |||
:2. for <math>t\ge 2e\mu</math>, | |||
::<math>\Pr[X\ge t]\le 2^{-t}.</math> | |||
}} | |||
{{Proof| To obtain the bounds in (1), we need to show that for <math>0<\delta< 1</math>, <math>\frac{e^{\delta}}{(1+\delta)^{(1+\delta)}}\le e^{-\delta^2/3}</math> and <math>\frac{e^{-\delta}}{(1-\delta)^{(1-\delta)}}\le e^{-\delta^2/2}</math>. We can verify both inequalities by standard analysis techniques. | |||
To obtain the bound in (2), let <math>t=(1+\delta)\mu</math>. Then <math>\delta=t/\mu-1\ge 2e-1</math>. Hence, | |||
:<math>\begin{align} | |||
\Pr[X\ge(1+\delta)\mu] | |||
&\le | |||
\left(\frac{e^\delta}{(1+\delta)^{(1+\delta)}}\right)^\mu\\ | |||
&\le | |||
\left(\frac{e}{1+\delta}\right)^{(1+\delta)\mu}\\ | |||
&\le | |||
\left(\frac{e}{2e}\right)^t\\ | |||
&\le | |||
2^{-t} | |||
\end{align}</math> | |||
}} | |||
== Balls into bins, revisited == | |||
Throwing <math>m</math> balls uniformly and independently to <math>n</math> bins, what is the maximum load of all bins with high probability? In the last class, we gave an analysis of this problem by using a counting argument. | |||
Now we give a more "advanced" analysis by using Chernoff bounds. | |||
For any <math>i\in[n]</math> and <math>j\in[m]</math>, let <math>X_{ij}</math> be the indicator variable for the event that ball <math>j</math> is thrown to bin <math>i</math>. Obviously | |||
:<math>\mathbf{E}[X_{ij}]=\Pr[\mbox{ball }j\mbox{ is thrown to bin }i]=\frac{1}{n}</math> | |||
Let <math>Y_i=\sum_{j\in[m]}X_{ij}</math> be the load of bin <math>i</math>. | |||
Then the expected load of bin <math>i</math> is | |||
<math>(*)\qquad \mu=\mathbf{E}[Y_i]=\mathbf{E}\left[\sum_{j\in[m]}X_{ij}\right]=\sum_{j\in[m]}\mathbf{E}[X_{ij}]=m/n. </math> | |||
For the case <math>m=n</math>, it holds that <math>\mu=1</math> | |||
Note that <math>Y_i</math> is a sum of <math>m</math> mutually independent indicator variable. Applying Chernoff bound, for any particular bin <math>i\in[n]</math>, | |||
:<math> | |||
\Pr[Y_i>(1+\delta)\mu] \le \left(\frac{e^{\delta}}{(1+\delta)^{1+\delta}}\right)^\mu. | |||
</math> | |||
=== When <math>m=n</math> === | |||
When <math>m=n</math>, <math>\mu=1</math>. Write <math>c=1+\delta</math>. The above bound can be written as | |||
:<math> | |||
\Pr[Y_i>c] \le \frac{e^{c-1}}{c^c}. | |||
</math> | |||
Let <math>c=\frac{e\ln n}{\ln\ln n}</math>, we evaluate <math>\frac{e^{c-1}}{c^c}</math> by taking logarithm to its reciprocal. | |||
:<math> | |||
\begin{align} | |||
\ln\left(\frac{c^c}{e^{c-1}}\right) | |||
&= | |||
c\ln c-c+1\\ | |||
&= | |||
c(\ln c-1)+1\\ | |||
&= | |||
\frac{e\ln n}{\ln\ln n}\left(\ln\ln n-\ln\ln\ln n\right)+1\\ | |||
&\ge | |||
\frac{e\ln n}{\ln\ln n}\cdot\frac{2}{e}\ln\ln n+1\\ | |||
&\ge | |||
2\ln n. | |||
\end{align} | |||
</math> | |||
Thus, | |||
:<math> | |||
\Pr\left[Y_i>\frac{e\ln n}{\ln\ln n}\right] \le \frac{1}{n^2}. | |||
</math> | |||
Applying the union bound, the probability that there exists a bin with load <math>>12\ln n</math> is | |||
:<math>n\cdot \Pr\left[Y_1>\frac{e\ln n}{\ln\ln n}\right] \le \frac{1}{n}</math>. | |||
Therefore, for <math>m=n</math>, with high probability, the maximum load is <math>O\left(\frac{e\ln n}{\ln\ln n}\right)</math>. | |||
=== For larger <math>m</math> === | |||
When <math>m\ge n\ln n</math>, then according to <math>(*)</math>, <math>\mu=\frac{m}{n}\ge \ln n</math> | |||
We can apply an easier form of the Chernoff bounds, | |||
:<math> | |||
\Pr[Y_i\ge 2e\mu]\le 2^{-2e\mu}\le 2^{-2e\ln n}<\frac{1}{n^2}. | |||
</math> | |||
By the union bound, the probability that there exists a bin with load <math>\ge 2e\frac{m}{n}</math> is, | |||
:<math>n\cdot \Pr\left[Y_1>2e\frac{m}{n}\right] = n\cdot \Pr\left[Y_1>2e\mu\right]\le \frac{1}{n}</math>. | |||
Therefore, for <math>m\ge n\ln n</math>, with high probability, the maximum load is <math>O\left(\frac{m}{n}\right)</math>. | |||
=Set Balancing= | |||
Supposed that we have an <math>n\times m</math> matrix <math>A</math> with 0-1 entries. We are looking for a <math>b\in\{-1,+1\}^m</math> that minimizes <math>\|Ab\|_\infty</math>. | |||
Recall that <math>\|\cdot\|_\infty</math> is the infinity norm (also called <math>L_\infty</math> norm) of a vector, and for the vector <math>c=Ab</math>, | |||
:<math>\|Ab\|_\infty=\max_{i=1,2,\ldots,n}|c_i|</math>. | |||
We can also describe this problem as an optimization: | |||
:<math>\begin{align} | |||
\mbox{minimize } | |||
&\quad | |||
\|Ab\|_\infty\\ | |||
\mbox{subject to: } | |||
&\quad | |||
b\in\{-1,+1\}^m. | |||
\end{align}</math> | |||
This problem is called set balancing for a reason. | |||
{|border="1" | |||
|The problem arises in designing statistical experiments. Suppose that we have <math>m</math> '''subjects''', each of which may have up to <math>n</math> '''features'''. This gives us an <math>n\times m</math> matrix <math>A</math>: | |||
:<math> | |||
\begin{array}{c} | |||
\mbox{feature 1:}\\ | |||
\mbox{feature 2:}\\ | |||
\vdots\\ | |||
\mbox{feature n:}\\ | |||
\end{array} | |||
\left[ | |||
\begin{array}{cccc} | |||
a_{11} & a_{12} & \cdots & a_{1m}\\ | |||
a_{21} & a_{22} & \cdots & a_{2m}\\ | |||
\vdots & \vdots & \ddots & \vdots\\ | |||
a_{n1} & a_{n2} & \cdots & a_{nm}\\ | |||
\end{array} | |||
\right], | |||
</math> | |||
where each column represents a subject and each row represent a feature. An entry <math>a_{ij}\in\{0,1\}</math> indicates whether subject <math>j</math> has feature <math>i</math>. | |||
By multiplying a vector <math>b\in\{-1,+1\}^m</math> | |||
:<math> | |||
\left[ | |||
\begin{array}{cccc} | |||
a_{11} & a_{12} & \cdots & a_{1m}\\ | |||
a_{21} & a_{22} & \cdots & a_{2m}\\ | |||
\vdots & \vdots & \ddots & \vdots\\ | |||
a_{n1} & a_{n2} & \cdots & a_{nm}\\ | |||
\end{array} | |||
\right] | |||
\left[ | |||
\begin{array}{c} | |||
b_{1}\\ | |||
b_{2}\\ | |||
\vdots\\ | |||
b_{m}\\ | |||
\end{array} | |||
\right] | |||
= | |||
\left[ | |||
\begin{array}{c} | |||
c_{1}\\ | |||
c_{2}\\ | |||
\vdots\\ | |||
c_{n}\\ | |||
\end{array} | |||
\right], | |||
</math> | |||
the subjects are partitioned into two disjoint groups: one for -1 and other other for +1. Each <math>c_i</math> gives the difference between the numbers of subjects with feature <math>i</math> in the two groups. By minimizing <math>\|Ab\|_\infty=\|c\|_\infty</math>, we ask for an optimal partition so that each feature is roughly as balanced as possible between the two groups. | |||
In a scientific experiment, one of the group serves as a [http://en.wikipedia.org/wiki/Scientific_control control group] (对照组). Ideally, we want the two groups are statistically identical, which is usually impossible to achieve in practice. The requirement of minimizing <math>\|Ab\|_\infty</math> actually means the statistical difference between the two groups are minimized. | |||
|} | |||
We propose an extremely simple "randomized algorithm" for computing a <math>b\in\{-1,+1\}^m</math>: for each <math>i=1,2,\ldots, m</math>, let <math>b_i</math> be independently chosen from <math>\{-1,+1\}</math>, such that | |||
:<math>b_i= | |||
\begin{cases} | |||
-1 & \mbox{with probability }\frac{1}{2}\\ | |||
+1 &\mbox{with probability }\frac{1}{2} | |||
\end{cases}. | |||
</math> | |||
This procedure can hardly be called as an "algorithm", because its decision is made disregard of the input <math>A</math>. We then show that despite of this obliviousness, the algorithm chooses a good enough <math>b</math>, such that for any <math>A</math>, <math>\|Ab\|_\infty=O(\sqrt{m\ln n})</math> with high probability. | |||
{{Theorem | |||
|Theorem| | |||
:Let <math>A</math> be an <math>n\times m</math> matrix with 0-1 entries. For a random vector <math>b</math> with <math>m</math> entries chosen independently and with equal probability from <math>\{-1,+1\}</math>, | |||
::<math>\Pr[\|Ab\|_\infty>2\sqrt{2m\ln n}]\le\frac{2}{n}</math>. | |||
}} | |||
{{Proof| | |||
Consider particularly the <math>i</math>-th row of <math>A</math>. The entry of <math>Ab</math> contributed by row <math>i</math> is <math>c_i=\sum_{j=1}^m a_{ij}b_j</math>. | |||
Let <math>k</math> be the non-zero entries in the row. If <math>k\le2\sqrt{2m\ln n}</math>, then clearly <math>|c_i|</math> is no greater than <math>2\sqrt{2m\ln n}</math>. On the other hand if <math>k>2\sqrt{2m\ln n}</math> then the <math>k</math> nonzero terms in the sum | |||
:<math>c_i=\sum_{j=1}^m a_{ij}b_j</math> | |||
are independent, each with probability 1/2 of being either +1 or -1. | |||
Thus, for these <math>k</math> nonzero terms, each <math>b_i</math> is either positive or negative independently with equal probability. There are expectedly <math>\mu=\frac{k}{2}</math> positive <math>b_i</math>'s among these <math>k</math> terms, and <math>c_i<-2\sqrt{2m\ln n}</math> only occurs when there are less than <math>\frac{k}{2}-\sqrt{2m\ln n}=\left(1-\delta\right)\mu</math> positive <math>b_i</math>'s, where <math>\delta=\frac{2\sqrt{2m\ln n}}{k}</math>. Applying Chernoff bound, this event occurs with probability at most | |||
:<math>\begin{align} | |||
\exp\left(-\frac{\mu\delta^2}{2}\right) | |||
&= | |||
\exp\left(-\frac{k}{2}\cdot\frac{8m\ln n}{2k^2}\right)\\ | |||
&= | |||
\exp\left(-\frac{2m\ln n}{k}\right)\\ | |||
&\le | |||
\exp\left(-\frac{2m\ln n}{m}\right)\\ | |||
&\le n^{-2}. | |||
\end{align} | |||
</math> | |||
The same argument can be applied to negative <math>b_i</math>'s, so that the probability that <math>c_i>2\sqrt{2m\ln n}</math> is at most <math>n^{-2}</math>. Therefore, by the union bound, | |||
:<math>\Pr[|c_i|> 2\sqrt{2m\ln n}]\le\frac{2}{n^2}</math>. | |||
Apply the union bound to all <math>n</math> rows. | |||
:<math>\Pr[\|Ab\|_\infty>2\sqrt{2m\ln n}]\le n\cdot\Pr[|c_i|> 2\sqrt{2m\ln n}]\le\frac{2}{n}</math>. | |||
}} | |||
How good is this randomized algorithm? In fact when <math>m=n</math> there exists a matrix <math>A</math> such that <math>\|Ab\|_\infty=\Omega(\sqrt{n})</math> for any choice of <math>b\in\{-1,+1\}^n</math>. | |||
Revision as of 11:10, 29 November 2015
The Chernoff Bound
Suppose that we have a fair coin. If we toss it once, then the outcome is completely unpredictable. But if we toss it, say for 1000 times, then the number of HEADs is very likely to be around 500. This striking phenomenon, illustrated in the right figure, is called the concentration. The Chernoff bound captures the concentration of independent trials.
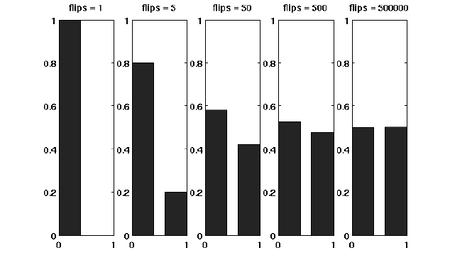
The Chernoff bound is also a tail bound for the sum of independent random variables which may give us exponentially sharp bounds.
Before proving the Chernoff bound, we should talk about the moment generating functions.
Moment generating functions
The more we know about the moments of a random variable [math]\displaystyle{ X }[/math], the more information we would have about [math]\displaystyle{ X }[/math]. There is a so-called moment generating function, which "packs" all the information about the moments of [math]\displaystyle{ X }[/math] into one function.
Definition - The moment generating function of a random variable [math]\displaystyle{ X }[/math] is defined as [math]\displaystyle{ \mathbf{E}\left[\mathrm{e}^{\lambda X}\right] }[/math] where [math]\displaystyle{ \lambda }[/math] is the parameter of the function.
By Taylor's expansion and the linearity of expectations,
- [math]\displaystyle{ \begin{align} \mathbf{E}\left[\mathrm{e}^{\lambda X}\right] &= \mathbf{E}\left[\sum_{k=0}^\infty\frac{\lambda^k}{k!}X^k\right]\\ &=\sum_{k=0}^\infty\frac{\lambda^k}{k!}\mathbf{E}\left[X^k\right] \end{align} }[/math]
The moment generating function [math]\displaystyle{ \mathbf{E}\left[\mathrm{e}^{\lambda X}\right] }[/math] is a function of [math]\displaystyle{ \lambda }[/math].
The Chernoff bound
The Chernoff bounds are exponentially sharp tail inequalities for the sum of independent trials. The bounds are obtained by applying Markov's inequality to the moment generating function of the sum of independent trials, with some appropriate choice of the parameter [math]\displaystyle{ \lambda }[/math].
Chernoff bound (the upper tail) - Let [math]\displaystyle{ X=\sum_{i=1}^n X_i }[/math], where [math]\displaystyle{ X_1, X_2, \ldots, X_n }[/math] are independent Poisson trials. Let [math]\displaystyle{ \mu=\mathbf{E}[X] }[/math].
- Then for any [math]\displaystyle{ \delta\gt 0 }[/math],
- [math]\displaystyle{ \Pr[X\ge (1+\delta)\mu]\le\left(\frac{e^{\delta}}{(1+\delta)^{(1+\delta)}}\right)^{\mu}. }[/math]
Proof. For any [math]\displaystyle{ \lambda\gt 0 }[/math], [math]\displaystyle{ X\ge (1+\delta)\mu }[/math] is equivalent to that [math]\displaystyle{ e^{\lambda X}\ge e^{\lambda (1+\delta)\mu} }[/math], thus - [math]\displaystyle{ \begin{align} \Pr[X\ge (1+\delta)\mu] &= \Pr\left[e^{\lambda X}\ge e^{\lambda (1+\delta)\mu}\right]\\ &\le \frac{\mathbf{E}\left[e^{\lambda X}\right]}{e^{\lambda (1+\delta)\mu}}, \end{align} }[/math]
where the last step follows by Markov's inequality.
Computing the moment generating function [math]\displaystyle{ \mathbf{E}[e^{\lambda X}] }[/math]:
- [math]\displaystyle{ \begin{align} \mathbf{E}\left[e^{\lambda X}\right] &= \mathbf{E}\left[e^{\lambda \sum_{i=1}^n X_i}\right]\\ &= \mathbf{E}\left[\prod_{i=1}^n e^{\lambda X_i}\right]\\ &= \prod_{i=1}^n \mathbf{E}\left[e^{\lambda X_i}\right]. & (\mbox{for independent random variables}) \end{align} }[/math]
Let [math]\displaystyle{ p_i=\Pr[X_i=1] }[/math] for [math]\displaystyle{ i=1,2,\ldots,n }[/math]. Then,
- [math]\displaystyle{ \mu=\mathbf{E}[X]=\mathbf{E}\left[\sum_{i=1}^n X_i\right]=\sum_{i=1}^n\mathbf{E}[X_i]=\sum_{i=1}^n p_i }[/math].
We bound the moment generating function for each individual [math]\displaystyle{ X_i }[/math] as follows.
- [math]\displaystyle{ \begin{align} \mathbf{E}\left[e^{\lambda X_i}\right] &= p_i\cdot e^{\lambda\cdot 1}+(1-p_i)\cdot e^{\lambda\cdot 0}\\ &= 1+p_i(e^\lambda -1)\\ &\le e^{p_i(e^\lambda-1)}, \end{align} }[/math]
where in the last step we apply the Taylor's expansion so that [math]\displaystyle{ e^y\ge 1+y }[/math] where [math]\displaystyle{ y=p_i(e^\lambda-1)\ge 0 }[/math]. (By doing this, we can transform the product to the sum of [math]\displaystyle{ p_i }[/math], which is [math]\displaystyle{ \mu }[/math].)
Therefore,
- [math]\displaystyle{ \begin{align} \mathbf{E}\left[e^{\lambda X}\right] &= \prod_{i=1}^n \mathbf{E}\left[e^{\lambda X_i}\right]\\ &\le \prod_{i=1}^n e^{p_i(e^\lambda-1)}\\ &= \exp\left(\sum_{i=1}^n p_i(e^{\lambda}-1)\right)\\ &= e^{(e^\lambda-1)\mu}. \end{align} }[/math]
Thus, we have shown that for any [math]\displaystyle{ \lambda\gt 0 }[/math],
- [math]\displaystyle{ \begin{align} \Pr[X\ge (1+\delta)\mu] &\le \frac{\mathbf{E}\left[e^{\lambda X}\right]}{e^{\lambda (1+\delta)\mu}}\\ &\le \frac{e^{(e^\lambda-1)\mu}}{e^{\lambda (1+\delta)\mu}}\\ &= \left(\frac{e^{(e^\lambda-1)}}{e^{\lambda (1+\delta)}}\right)^\mu \end{align} }[/math].
For any [math]\displaystyle{ \delta\gt 0 }[/math], we can let [math]\displaystyle{ \lambda=\ln(1+\delta)\gt 0 }[/math] to get
- [math]\displaystyle{ \Pr[X\ge (1+\delta)\mu]\le\left(\frac{e^{\delta}}{(1+\delta)^{(1+\delta)}}\right)^{\mu}. }[/math]
- [math]\displaystyle{ \square }[/math]
The idea of the proof is actually quite clear: we apply Markov's inequality to [math]\displaystyle{ e^{\lambda X} }[/math] and for the rest, we just estimate the moment generating function [math]\displaystyle{ \mathbf{E}[e^{\lambda X}] }[/math]. To make the bound as tight as possible, we minimized the [math]\displaystyle{ \frac{e^{(e^\lambda-1)}}{e^{\lambda (1+\delta)}} }[/math] by setting [math]\displaystyle{ \lambda=\ln(1+\delta) }[/math], which can be justified by taking derivatives of [math]\displaystyle{ \frac{e^{(e^\lambda-1)}}{e^{\lambda (1+\delta)}} }[/math].
We then proceed to the lower tail, the probability that the random variable deviates below the mean value:
Chernoff bound (the lower tail) - Let [math]\displaystyle{ X=\sum_{i=1}^n X_i }[/math], where [math]\displaystyle{ X_1, X_2, \ldots, X_n }[/math] are independent Poisson trials. Let [math]\displaystyle{ \mu=\mathbf{E}[X] }[/math].
- Then for any [math]\displaystyle{ 0\lt \delta\lt 1 }[/math],
- [math]\displaystyle{ \Pr[X\le (1-\delta)\mu]\le\left(\frac{e^{-\delta}}{(1-\delta)^{(1-\delta)}}\right)^{\mu}. }[/math]
Proof. For any [math]\displaystyle{ \lambda\lt 0 }[/math], by the same analysis as in the upper tail version, - [math]\displaystyle{ \begin{align} \Pr[X\le (1-\delta)\mu] &= \Pr\left[e^{\lambda X}\ge e^{\lambda (1-\delta)\mu}\right]\\ &\le \frac{\mathbf{E}\left[e^{\lambda X}\right]}{e^{\lambda (1-\delta)\mu}}\\ &\le \left(\frac{e^{(e^\lambda-1)}}{e^{\lambda (1-\delta)}}\right)^\mu. \end{align} }[/math]
For any [math]\displaystyle{ 0\lt \delta\lt 1 }[/math], we can let [math]\displaystyle{ \lambda=\ln(1-\delta)\lt 0 }[/math] to get
- [math]\displaystyle{ \Pr[X\ge (1-\delta)\mu]\le\left(\frac{e^{-\delta}}{(1-\delta)^{(1-\delta)}}\right)^{\mu}. }[/math]
- [math]\displaystyle{ \square }[/math]
Some useful special forms of the bounds can be derived directly from the above general forms of the bounds. We now know better why we say that the bounds are exponentially sharp.
Useful forms of the Chernoff bound - Let [math]\displaystyle{ X=\sum_{i=1}^n X_i }[/math], where [math]\displaystyle{ X_1, X_2, \ldots, X_n }[/math] are independent Poisson trials. Let [math]\displaystyle{ \mu=\mathbf{E}[X] }[/math]. Then
- 1. for [math]\displaystyle{ 0\lt \delta\le 1 }[/math],
- [math]\displaystyle{ \Pr[X\ge (1+\delta)\mu]\lt \exp\left(-\frac{\mu\delta^2}{3}\right); }[/math]
- [math]\displaystyle{ \Pr[X\le (1-\delta)\mu]\lt \exp\left(-\frac{\mu\delta^2}{2}\right); }[/math]
- 2. for [math]\displaystyle{ t\ge 2e\mu }[/math],
- [math]\displaystyle{ \Pr[X\ge t]\le 2^{-t}. }[/math]
Proof. To obtain the bounds in (1), we need to show that for [math]\displaystyle{ 0\lt \delta\lt 1 }[/math], [math]\displaystyle{ \frac{e^{\delta}}{(1+\delta)^{(1+\delta)}}\le e^{-\delta^2/3} }[/math] and [math]\displaystyle{ \frac{e^{-\delta}}{(1-\delta)^{(1-\delta)}}\le e^{-\delta^2/2} }[/math]. We can verify both inequalities by standard analysis techniques. To obtain the bound in (2), let [math]\displaystyle{ t=(1+\delta)\mu }[/math]. Then [math]\displaystyle{ \delta=t/\mu-1\ge 2e-1 }[/math]. Hence,
- [math]\displaystyle{ \begin{align} \Pr[X\ge(1+\delta)\mu] &\le \left(\frac{e^\delta}{(1+\delta)^{(1+\delta)}}\right)^\mu\\ &\le \left(\frac{e}{1+\delta}\right)^{(1+\delta)\mu}\\ &\le \left(\frac{e}{2e}\right)^t\\ &\le 2^{-t} \end{align} }[/math]
- [math]\displaystyle{ \square }[/math]
Balls into bins, revisited
Throwing [math]\displaystyle{ m }[/math] balls uniformly and independently to [math]\displaystyle{ n }[/math] bins, what is the maximum load of all bins with high probability? In the last class, we gave an analysis of this problem by using a counting argument.
Now we give a more "advanced" analysis by using Chernoff bounds.
For any [math]\displaystyle{ i\in[n] }[/math] and [math]\displaystyle{ j\in[m] }[/math], let [math]\displaystyle{ X_{ij} }[/math] be the indicator variable for the event that ball [math]\displaystyle{ j }[/math] is thrown to bin [math]\displaystyle{ i }[/math]. Obviously
- [math]\displaystyle{ \mathbf{E}[X_{ij}]=\Pr[\mbox{ball }j\mbox{ is thrown to bin }i]=\frac{1}{n} }[/math]
Let [math]\displaystyle{ Y_i=\sum_{j\in[m]}X_{ij} }[/math] be the load of bin [math]\displaystyle{ i }[/math].
Then the expected load of bin [math]\displaystyle{ i }[/math] is
[math]\displaystyle{ (*)\qquad \mu=\mathbf{E}[Y_i]=\mathbf{E}\left[\sum_{j\in[m]}X_{ij}\right]=\sum_{j\in[m]}\mathbf{E}[X_{ij}]=m/n. }[/math]
For the case [math]\displaystyle{ m=n }[/math], it holds that [math]\displaystyle{ \mu=1 }[/math]
Note that [math]\displaystyle{ Y_i }[/math] is a sum of [math]\displaystyle{ m }[/math] mutually independent indicator variable. Applying Chernoff bound, for any particular bin [math]\displaystyle{ i\in[n] }[/math],
- [math]\displaystyle{ \Pr[Y_i\gt (1+\delta)\mu] \le \left(\frac{e^{\delta}}{(1+\delta)^{1+\delta}}\right)^\mu. }[/math]
When [math]\displaystyle{ m=n }[/math]
When [math]\displaystyle{ m=n }[/math], [math]\displaystyle{ \mu=1 }[/math]. Write [math]\displaystyle{ c=1+\delta }[/math]. The above bound can be written as
- [math]\displaystyle{ \Pr[Y_i\gt c] \le \frac{e^{c-1}}{c^c}. }[/math]
Let [math]\displaystyle{ c=\frac{e\ln n}{\ln\ln n} }[/math], we evaluate [math]\displaystyle{ \frac{e^{c-1}}{c^c} }[/math] by taking logarithm to its reciprocal.
- [math]\displaystyle{ \begin{align} \ln\left(\frac{c^c}{e^{c-1}}\right) &= c\ln c-c+1\\ &= c(\ln c-1)+1\\ &= \frac{e\ln n}{\ln\ln n}\left(\ln\ln n-\ln\ln\ln n\right)+1\\ &\ge \frac{e\ln n}{\ln\ln n}\cdot\frac{2}{e}\ln\ln n+1\\ &\ge 2\ln n. \end{align} }[/math]
Thus,
- [math]\displaystyle{ \Pr\left[Y_i\gt \frac{e\ln n}{\ln\ln n}\right] \le \frac{1}{n^2}. }[/math]
Applying the union bound, the probability that there exists a bin with load [math]\displaystyle{ \gt 12\ln n }[/math] is
- [math]\displaystyle{ n\cdot \Pr\left[Y_1\gt \frac{e\ln n}{\ln\ln n}\right] \le \frac{1}{n} }[/math].
Therefore, for [math]\displaystyle{ m=n }[/math], with high probability, the maximum load is [math]\displaystyle{ O\left(\frac{e\ln n}{\ln\ln n}\right) }[/math].
For larger [math]\displaystyle{ m }[/math]
When [math]\displaystyle{ m\ge n\ln n }[/math], then according to [math]\displaystyle{ (*) }[/math], [math]\displaystyle{ \mu=\frac{m}{n}\ge \ln n }[/math]
We can apply an easier form of the Chernoff bounds,
- [math]\displaystyle{ \Pr[Y_i\ge 2e\mu]\le 2^{-2e\mu}\le 2^{-2e\ln n}\lt \frac{1}{n^2}. }[/math]
By the union bound, the probability that there exists a bin with load [math]\displaystyle{ \ge 2e\frac{m}{n} }[/math] is,
- [math]\displaystyle{ n\cdot \Pr\left[Y_1\gt 2e\frac{m}{n}\right] = n\cdot \Pr\left[Y_1\gt 2e\mu\right]\le \frac{1}{n} }[/math].
Therefore, for [math]\displaystyle{ m\ge n\ln n }[/math], with high probability, the maximum load is [math]\displaystyle{ O\left(\frac{m}{n}\right) }[/math].
Set Balancing
Supposed that we have an [math]\displaystyle{ n\times m }[/math] matrix [math]\displaystyle{ A }[/math] with 0-1 entries. We are looking for a [math]\displaystyle{ b\in\{-1,+1\}^m }[/math] that minimizes [math]\displaystyle{ \|Ab\|_\infty }[/math].
Recall that [math]\displaystyle{ \|\cdot\|_\infty }[/math] is the infinity norm (also called [math]\displaystyle{ L_\infty }[/math] norm) of a vector, and for the vector [math]\displaystyle{ c=Ab }[/math],
- [math]\displaystyle{ \|Ab\|_\infty=\max_{i=1,2,\ldots,n}|c_i| }[/math].
We can also describe this problem as an optimization:
- [math]\displaystyle{ \begin{align} \mbox{minimize } &\quad \|Ab\|_\infty\\ \mbox{subject to: } &\quad b\in\{-1,+1\}^m. \end{align} }[/math]
This problem is called set balancing for a reason.
The problem arises in designing statistical experiments. Suppose that we have [math]\displaystyle{ m }[/math] subjects, each of which may have up to [math]\displaystyle{ n }[/math] features. This gives us an [math]\displaystyle{ n\times m }[/math] matrix [math]\displaystyle{ A }[/math]:
where each column represents a subject and each row represent a feature. An entry [math]\displaystyle{ a_{ij}\in\{0,1\} }[/math] indicates whether subject [math]\displaystyle{ j }[/math] has feature [math]\displaystyle{ i }[/math]. By multiplying a vector [math]\displaystyle{ b\in\{-1,+1\}^m }[/math]
the subjects are partitioned into two disjoint groups: one for -1 and other other for +1. Each [math]\displaystyle{ c_i }[/math] gives the difference between the numbers of subjects with feature [math]\displaystyle{ i }[/math] in the two groups. By minimizing [math]\displaystyle{ \|Ab\|_\infty=\|c\|_\infty }[/math], we ask for an optimal partition so that each feature is roughly as balanced as possible between the two groups. In a scientific experiment, one of the group serves as a control group (对照组). Ideally, we want the two groups are statistically identical, which is usually impossible to achieve in practice. The requirement of minimizing [math]\displaystyle{ \|Ab\|_\infty }[/math] actually means the statistical difference between the two groups are minimized. |
We propose an extremely simple "randomized algorithm" for computing a [math]\displaystyle{ b\in\{-1,+1\}^m }[/math]: for each [math]\displaystyle{ i=1,2,\ldots, m }[/math], let [math]\displaystyle{ b_i }[/math] be independently chosen from [math]\displaystyle{ \{-1,+1\} }[/math], such that
- [math]\displaystyle{ b_i= \begin{cases} -1 & \mbox{with probability }\frac{1}{2}\\ +1 &\mbox{with probability }\frac{1}{2} \end{cases}. }[/math]
This procedure can hardly be called as an "algorithm", because its decision is made disregard of the input [math]\displaystyle{ A }[/math]. We then show that despite of this obliviousness, the algorithm chooses a good enough [math]\displaystyle{ b }[/math], such that for any [math]\displaystyle{ A }[/math], [math]\displaystyle{ \|Ab\|_\infty=O(\sqrt{m\ln n}) }[/math] with high probability.
Theorem - Let [math]\displaystyle{ A }[/math] be an [math]\displaystyle{ n\times m }[/math] matrix with 0-1 entries. For a random vector [math]\displaystyle{ b }[/math] with [math]\displaystyle{ m }[/math] entries chosen independently and with equal probability from [math]\displaystyle{ \{-1,+1\} }[/math],
- [math]\displaystyle{ \Pr[\|Ab\|_\infty\gt 2\sqrt{2m\ln n}]\le\frac{2}{n} }[/math].
- Let [math]\displaystyle{ A }[/math] be an [math]\displaystyle{ n\times m }[/math] matrix with 0-1 entries. For a random vector [math]\displaystyle{ b }[/math] with [math]\displaystyle{ m }[/math] entries chosen independently and with equal probability from [math]\displaystyle{ \{-1,+1\} }[/math],
Proof. Consider particularly the [math]\displaystyle{ i }[/math]-th row of [math]\displaystyle{ A }[/math]. The entry of [math]\displaystyle{ Ab }[/math] contributed by row [math]\displaystyle{ i }[/math] is [math]\displaystyle{ c_i=\sum_{j=1}^m a_{ij}b_j }[/math].
Let [math]\displaystyle{ k }[/math] be the non-zero entries in the row. If [math]\displaystyle{ k\le2\sqrt{2m\ln n} }[/math], then clearly [math]\displaystyle{ |c_i| }[/math] is no greater than [math]\displaystyle{ 2\sqrt{2m\ln n} }[/math]. On the other hand if [math]\displaystyle{ k\gt 2\sqrt{2m\ln n} }[/math] then the [math]\displaystyle{ k }[/math] nonzero terms in the sum
- [math]\displaystyle{ c_i=\sum_{j=1}^m a_{ij}b_j }[/math]
are independent, each with probability 1/2 of being either +1 or -1.
Thus, for these [math]\displaystyle{ k }[/math] nonzero terms, each [math]\displaystyle{ b_i }[/math] is either positive or negative independently with equal probability. There are expectedly [math]\displaystyle{ \mu=\frac{k}{2} }[/math] positive [math]\displaystyle{ b_i }[/math]'s among these [math]\displaystyle{ k }[/math] terms, and [math]\displaystyle{ c_i\lt -2\sqrt{2m\ln n} }[/math] only occurs when there are less than [math]\displaystyle{ \frac{k}{2}-\sqrt{2m\ln n}=\left(1-\delta\right)\mu }[/math] positive [math]\displaystyle{ b_i }[/math]'s, where [math]\displaystyle{ \delta=\frac{2\sqrt{2m\ln n}}{k} }[/math]. Applying Chernoff bound, this event occurs with probability at most
- [math]\displaystyle{ \begin{align} \exp\left(-\frac{\mu\delta^2}{2}\right) &= \exp\left(-\frac{k}{2}\cdot\frac{8m\ln n}{2k^2}\right)\\ &= \exp\left(-\frac{2m\ln n}{k}\right)\\ &\le \exp\left(-\frac{2m\ln n}{m}\right)\\ &\le n^{-2}. \end{align} }[/math]
The same argument can be applied to negative [math]\displaystyle{ b_i }[/math]'s, so that the probability that [math]\displaystyle{ c_i\gt 2\sqrt{2m\ln n} }[/math] is at most [math]\displaystyle{ n^{-2} }[/math]. Therefore, by the union bound,
- [math]\displaystyle{ \Pr[|c_i|\gt 2\sqrt{2m\ln n}]\le\frac{2}{n^2} }[/math].
Apply the union bound to all [math]\displaystyle{ n }[/math] rows.
- [math]\displaystyle{ \Pr[\|Ab\|_\infty\gt 2\sqrt{2m\ln n}]\le n\cdot\Pr[|c_i|\gt 2\sqrt{2m\ln n}]\le\frac{2}{n} }[/math].
- [math]\displaystyle{ \square }[/math]
How good is this randomized algorithm? In fact when [math]\displaystyle{ m=n }[/math] there exists a matrix [math]\displaystyle{ A }[/math] such that [math]\displaystyle{ \|Ab\|_\infty=\Omega(\sqrt{n}) }[/math] for any choice of [math]\displaystyle{ b\in\{-1,+1\}^n }[/math].