组合数学 (Fall 2011) and 组合数学 (Fall 2011)/Sieve methods: Difference between pages
imported>Etone |
imported>Etone |
||
| Line 1: | Line 1: | ||
| | == Principle of Inclusion-Exclusion == | ||
| | Let <math>A</math> and <math>B</math> be two finite sets. The cardinality of their union is | ||
| | :<math>|A\cup B|=|A|+|B|-{\color{Blue}|A\cap B|}</math>. | ||
For three sets <math>A</math>, <math>B</math>, and <math>C</math>, the cardinality of the union of these three sets is computed as | |||
| | :<math>|A\cup B\cup C|=|A|+|B|+|C|-{\color{Blue}|A\cap B|}-{\color{Blue}|A\cap C|}-{\color{Blue}|B\cap C|}+{\color{Red}|A\cap B\cap C|}</math>. | ||
| | This is illustrated by the following figure. | ||
| | ::[[Image:Inclusion-exclusion.png|200px|border|center]] | ||
| | Generally, the '''Principle of Inclusion-Exclusion''' states the rule for computing the union of <math>n</math> finite sets <math>A_1,A_2,\ldots,A_n</math>, such that | ||
{{Equation| | |||
| | <math> | ||
| | \begin{align} | ||
| | \left|\bigcup_{i=1}^nA_i\right| | ||
| | &= | ||
\sum_{I\subseteq\{1,\ldots,n\}}(-1)^{|I|-1}\left|\bigcap_{i\in I}A_i\right|. | |||
| | \end{align} | ||
</math> | |||
| | }} | ||
| | ----- | ||
| | |||
| | In combinatorial enumeration, the Principle of Inclusion-Exclusion is usually applied in its complement form. | ||
| | |||
| | Let <math>A_1,A_2,\ldots,A_n\subseteq U</math> be subsets of some finite set <math>U</math>. Here <math>U</math> is some universe of combinatorial objects, whose cardinality is easy to calculate (e.g. all strings, tuples, permutations), and each <math>A_i</math> contains the objects with some specific property (e.g. a "pattern") which we want to avoid. The problem is to count the number of objects without any of the <math>n</math> properties. We write <math>\bar{A_i}=U-A_i</math>. The number of objects without any of the properties <math>A_1,A_2,\ldots,A_n</math> is | ||
| | {{Equation| | ||
| | <math> | ||
| | \begin{align} | ||
| | \left|\bar{A_1}\cap\bar{A_2}\cap\cdots\cap\bar{A_n}\right|=\left|U-\bigcup_{i=1}^nA_i\right| | ||
| | &= | ||
|U|+\sum_{I\subseteq\{1,\ldots,n\}}(-1)^{|I|}\left|\bigcap_{i\in I}A_i\right|. | |||
| | \end{align} | ||
</math> | |||
}} | |||
| | For an <math>I\subseteq\{1,2,\ldots,n\}</math>, we denote | ||
| | :<math>A_I=\bigcap_{i\in I}A_i</math> | ||
| | with the convention that <math>A_\emptyset=U</math>. The above equation is stated as: | ||
| | {{Theorem|Principle of Inclusion-Exclusion| | ||
| | :Let <math>A_1,A_2,\ldots,A_n</math> be a family of subsets of <math>U</math>. Then the number of elements of <math>U</math> which lie in none of the subsets <math>A_i</math> is | ||
| | ::<math>\sum_{I\subseteq\{1,\ldots, n\}}(-1)^{|I|}|A_I|</math>. | ||
}} | |||
Let <math>S_k=\sum_{|I|=k}|A_I|\,</math>. Conventionally, <math>S_0=|A_\emptyset|=|U|</math>. The principle of inclusion-exclusion can be expressed as | |||
{{Equation|<math> | |||
S_0-S_1+S_2+\cdots+(-1)^nS_n. | |||
</math> | |||
}} | |||
=== Surjections === | |||
In the twelvefold way, we discuss the counting problems incurred by the mappings <math>f:N\rightarrow M</math>. The basic case is that elements from both <math>N</math> and <math>M</math> are distinguishable. In this case, it is easy to count the number of arbitrary mappings (which is <math>m^n</math>) and the number of injective (one-to-one) mappings (which is <math>(m)_n</math>), but the number of surjective is difficult. Here we apply the principle of inclusion-exclusion to count the number of surjective (onto) mappings. | |||
{{Theorem|Theorem| | |||
:The number of surjective mappings from an <math>n</math>-set to an <math>m</math>-set is given by | |||
::<math>\sum_{k=1}^m(-1)^{m-k}{m\choose k}k^n</math>. | |||
}} | |||
{{Proof| | |||
Let <math>U=\{f:[n]\rightarrow[m]\}</math> be the set of mappings from <math>[n]</math> to <math>[m]</math>. Then <math>|U|=m^n</math>. | |||
For <math>i\in[m]</math>, let <math>A_i</math> be the set of mappings <math>f:[n]\rightarrow[m]</math> that none of <math>j\in[n]</math> is mapped to <math>i</math>, i.e. <math>A_i=\{f:[n]\rightarrow[m]\setminus\{i\}\}</math>, thus <math>|A_i|=(m-1)^n</math>. | |||
More generally, for <math>I\subseteq [m]</math>, <math>A_I=\bigcap_{i\in I}A_i</math> contains the mappings <math>f:[n]\rightarrow[m]\setminus I</math>. And <math>|A_I|=(m-|I|)^n\,</math>. | |||
A mapping <math>f:[n]\rightarrow[m]</math> is surjective if <math>f</math> lies in none of <math>A_i</math>. By the principle of inclusion-exclusion, the number of surjective <math>f:[n]\rightarrow[m]</math> is | |||
:<math>\sum_{I\subseteq[m]}(-1)^{|I|}\left|A_I\right|=\sum_{I\subseteq[m]}(-1)^{|I|}(m-|I|)^n=\sum_{j=0}^m(-1)^j{m\choose j}(m-j)^n</math>. | |||
Let <math>k=m-j</math>. The theorem is proved. | |||
}} | |||
Recall that, in the twelvefold way, we establish a relation between surjections and partitions. | |||
* Surjection to ordered partition: | |||
:For a surjective <math>f:[n]\rightarrow[m]</math>, <math>(f^{-1}(0),f^{-1}(1),\ldots,f^{-1}(m-1))</math> is an '''ordered partition''' of <math>[n]</math>. | |||
* Ordered partition to surjection: | |||
:For an ordered <math>m</math>-partition <math>(B_0,B_1,\ldots, B_{m-1})</math> of <math>[n]</math>, we can define a function <math>f:[n]\rightarrow[m]</math> by letting <math>f(i)=j</math> if and only if <math>i\in B_j</math>. <math>f</math> is surjective since as a partition, none of <math>B_i</math> is empty. | |||
Therefore, we have a one-to-one correspondence between surjective mappings from an <math>n</math>-set to an <math>m</math>-set and the ordered <math>m</math>-partitions of an <math>n</math>-set. | |||
The Stirling number of the second kind <math>S(n,m)</math> is the number of <math>m</math>-partitions of an <math>n</math>-set. There are <math>m!</math> ways to order an <math>m</math>-partition, thus the number of surjective mappings <math>f:[n]\rightarrow[m]</math> is <math>m! S(n,m)</math>. Combining with what we have proved for surjections, we give the following result for the Stirling number of the second kind. | |||
{{Theorem|Proposition| | |||
:<math>S(n,m)=\frac{1}{m!}\sum_{k=1}^m(-1)^{m-k}{m\choose k}k^n</math>. | |||
}} | |||
=== Derangements === | |||
We now count the number of bijections from a set to itself with no fixed points. This is the '''derangement problem'''. | |||
For a permutation <math>\pi</math> of <math>\{1,2,\ldots,n\}</math>, a '''fixed point''' is such an <math>i\in\{1,2,\ldots,n\}</math> that <math>\pi(i)=i</math>. | |||
A [http://en.wikipedia.org/wiki/Derangement '''derangement'''] of <math>\{1,2,\ldots,n\}</math> is a permutation of <math>\{1,2,\ldots,n\}</math> that has no fixed points. | |||
{{Theorem|Theorem| | |||
:The number of derangements of <math>\{1,2,\ldots,n\}</math> given by | |||
::<math>n!\sum_{k=0}^n\frac{(-1)^k}{k!}\approx \frac{n!}{\mathrm{e}}</math>. | |||
}} | |||
{{Proof| | |||
Let <math>U</math> be the set of all permutations of <math>\{1,2,\ldots,n\}</math>. So <math>|U|=n!</math>. | |||
Let <math>A_i</math> be the set of permutations with fixed point <math>i</math>; so <math>|A_i|=(n-1)!</math>. More generally, for any <math>I\subseteq \{1,2,\ldots,n\}</math>, <math>A_I=\bigcap_{i\in I}A_i</math>, and <math>|A_I|=(n-|I|)!</math>, since permutations in <math>A_I</math> fix every point in <math>I</math> and permute the remaining points arbitrarily. A permutation is a derangement if and only if it lies in none of the sets <math>A_i</math>. So the number of derangements is | |||
:<math>\sum_{I\subseteq\{1,2,\ldots,n\}}(-1)^{|I|}(n-|I|)!=\sum_{k=0}^n(-1)^k{n\choose k}(n-k)!=n!\sum_{k=0}^n\frac{(-1)^k}{k!}.</math> | |||
By Taylor's series, | |||
:<math>\frac{1}{\mathrm{e}}=\sum_{k=0}^\infty\frac{(-1)^k}{k!}=\sum_{k=0}^n\frac{(-1)^k}{k!}\pm o\left(\frac{1}{n!}\right)</math>. | |||
It is not hard to see that <math>n!\sum_{k=0}^n\frac{(-1)^k}{k!}</math> is the closest integer to <math>\frac{n!}{\mathrm{e}}</math>. | |||
}} | |||
Therefore, there are about <math>\frac{1}{\mathrm{e}}</math> fraction of all permutations with no fixed points. | |||
=== Permutations with restricted positions === | |||
We introduce a general theory of counting permutations with restricted positions. In the derangement problem, we count the number of permutations that <math>\pi(i)\neq i</math>. We now generalize to the problem of counting permutations which avoid a set of arbitrarily specified positions. | |||
| | It is traditionally described using terminology from the game of chess. Let <math>B\subseteq \{1,\ldots,n\}\times \{1,\ldots,n\}</math>, called a '''board'''. As illustrated below, we can think of <math>B</math> as a chess board, with the positions in <math>B</math> marked by "<math>\times</math>". | ||
| | {{Chess diagram small | ||
| | |||
| | |||
|= | |||
8 |__|xx|xx|__|xx|__|__|xx|= | |||
7 |xx|__|__|xx|__|__|xx|__|= | |||
6 |xx|__|xx|xx|__|xx|xx|__|= | |||
5 |__|xx|__|__|xx|__|xx|__|= | |||
4 |xx|__|__|__|xx|xx|xx|__|= | |||
3 |__|xx|__|xx|__|__|__|xx|= | |||
2 |__|__|xx|__|xx|__|__|xx|= | |||
1 |xx|__|__|xx|__|xx|__|__|= | |||
a b c d e f g h | |||
| | |||
}} | }} | ||
For a permutation <math>\pi</math> of <math>\{1,\ldots,n\}</math>, define the '''graph''' <math>G_\pi(V,E)</math> as | |||
:<math> | |||
\begin{align} | |||
G_\pi &= \{(i,\pi(i))\mid i\in \{1,2,\ldots,n\}\}. | |||
\end{align} | |||
</math> | |||
This can also be viewed as a set of marked positions on a chess board. Each row and each column has only one marked position, because <math>\pi</math> is a permutation. Thus, we can identify each <math>G_\pi</math> as a placement of <math>n</math> rooks (“城堡”,规则同中国象棋里的“车”) without attacking each other. | |||
For example, the following is the <math>G_\pi</math> of such <math>\pi</math> that <math>\pi(i)=i</math>. | |||
{{Chess diagram small | |||
| | |||
| | |||
|= | |||
8 |rl|__|__|__|__|__|__|__|= | |||
7 |__|rl|__|__|__|__|__|__|= | |||
6 |__|__|rl|__|__|__|__|__|= | |||
5 |__|__|__|rl|__|__|__|__|= | |||
4 |__|__|__|__|rl|__|__|__|= | |||
3 |__|__|__|__|__|rl|__|__|= | |||
2 |__|__|__|__|__|__|rl|__|= | |||
1 |__|__|__|__|__|__|__|rl|= | |||
a b c d e f g h | |||
| | |||
}} | |||
Now define | |||
:<math>\begin{align} | |||
N_0 &= \left|\left\{\pi\mid B\cap G_\pi=\emptyset\right\}\right|\\ | |||
r_k &= \mbox{number of }k\mbox{-subsets of }B\mbox{ such that no two elements have a common coordinate}\\ | |||
&=\left|\left\{S\in{B\choose k} \,\bigg|\, \forall (i_1,j_1),(i_2,j_2)\in S, i_1\neq i_2, j_1\neq j_2 \right\}\right| | |||
\end{align} | |||
</math> | |||
Interpreted in chess game, | |||
* <math>B</math>: a set of marked positions in an <math>[n]\times [n]</math> chess board. | |||
* <math>N_0</math>: the number of ways of placing <math>n</math> non-attacking rooks on the chess board such that none of these rooks lie in <math>B</math>. | |||
* <math>r_k</math>: number of ways of placing <math>k</math> non-attacking rooks on <math>B</math>. | |||
Our goal is to count <math>N_0</math> in terms of <math>r_k</math>. This gives the number of permutations avoid all positions in a <math>B</math>. | |||
= | {{Theorem|Theorem| | ||
:<math>N_0=\sum_{k=0}^n(-1)^kr_k(n-k)!</math>. | |||
}} | |||
{{Proof| | |||
For each <math>i\in[n]</math>, let <math>A_i=\{\pi\mid (i,\pi(i))\in B\}</math> be the set of permutations <math>\pi</math> whose <math>i</math>-th position is in <math>B</math>. | |||
<math>N_0</math> is the number of permutations avoid all positions in <math>B</math>. Thus, our goal is to count the number of permutations <math>\pi</math> in none of <math>A_i</math> for <math>i\in [n]</math>. | |||
= | For each <math>I\subseteq [n]</math>, let <math>A_I=\bigcap_{i\in I}A_i</math>, which is the set of permutations <math>\pi</math> such that <math>(i,\pi(i))\in B</math> for all <math>i\in I</math>. Due to the principle of inclusion-exclusion, | ||
:<math>N_0=\sum_{I\subseteq [n]} (-1)^{|I|}|A_I|=\sum_{k=0}^n(-1)^k\sum_{I\in{[n]\choose k}}|A_I|</math>. | |||
= | The next observation is that | ||
:<math>\sum_{I\in{[n]\choose k}}|A_I|=r_k(n-k)!</math>, | |||
because we can count both sides by first placing <math>k</math> non-attacking rooks on <math>B</math> and placing <math>n-k</math> additional non-attacking rooks on <math>[n]\times [n]</math> in <math>(n-k)!</math> ways. | |||
== | Therefore, | ||
:<math>N_0=\sum_{k=0}^n(-1)^kr_k(n-k)!</math>. | |||
}} | |||
=== | ====Derangement problem==== | ||
We use the above general method to solve the derange problem again. | |||
= | Take <math>B=\{(1,1),(2,2),\ldots,(n,n)\}</math> as the chess board. A derangement <math>\pi</math> is a placement of <math>n</math> non-attacking rooks such that none of them is in <math>B</math>. | ||
{{Chess diagram small | |||
| | |||
| | |||
|= | |||
8 |xx|__|__|__|__|__|__|__|= | |||
7 |__|xx|__|__|__|__|__|__|= | |||
6 |__|__|xx|__|__|__|__|__|= | |||
5 |__|__|__|xx|__|__|__|__|= | |||
4 |__|__|__|__|xx|__|__|__|= | |||
3 |__|__|__|__|__|xx|__|__|= | |||
2 |__|__|__|__|__|__|xx|__|= | |||
1 |__|__|__|__|__|__|__|xx|= | |||
a b c d e f g h | |||
| | |||
}} | |||
Clearly, the number of ways of placing <math>k</math> non-attacking rooks on <math>B</math> is <math>r_k={n\choose k}</math>. We want to count <math>N_0</math>, which gives the number of ways of placing <math>n</math> non-attacking rooks such that none of these rooks lie in <math>B</math>. | |||
By the above theorem | |||
:<math> | |||
N_0=\sum_{k=0}^n(-1)^kr_k(n-k)!=\sum_{k=0}^n(-1)^k{n\choose k}(n-k)!=\sum_{k=0}^n(-1)^k\frac{n!}{k!}=n!\sum_{k=0}^n(-1)^k\frac{1}{k!}\approx\frac{n!}{e}. | |||
</math> | |||
====Problème des ménages==== | |||
Suppose that in a banquet, we want to seat <math>n</math> couples at a circular table, satisfying the following constraints: | |||
* Men and women are in alternate places. | |||
* No one sits next to his/her spouse. | |||
In how many ways can this be done? | |||
(For convenience, we assume that every seat at the table marked differently so that rotating the seats clockwise or anti-clockwise will end up with a '''different''' solution.) | |||
First, let the <math>n</math> ladies find their seats. They may either sit at the odd numbered seats or even numbered seats, in either case, there are <math>n!</math> different orders. Thus, there are <math>2(n!)</math> ways to seat the <math>n</math> ladies. | |||
After sitting the wives, we label the remaining <math>n</math> places clockwise as <math>0,1,\ldots, n-1</math>. And a seating of the <math>n</math> husbands is given by a permutation <math>\pi</math> of <math>[n]</math> defined as follows. Let <math>\pi(i)</math> be the seat of the husband of he lady sitting at the <math>i</math>-th place. | |||
It is easy to see that <math>\pi</math> satisfies that <math>\pi(i)\neq i</math> and <math>\pi(i)\not\equiv i+1\pmod n</math>, and every permutation <math>\pi</math> with these properties gives a feasible seating of the <math>n</math> husbands. Thus, we only need to count the number of permutations <math>\pi</math> such that <math>\pi(i)\not\equiv i, i+1\pmod n</math>. | |||
Take <math>B=\{(0,0),(1,1),\ldots,(n-1,n-1), (0,1),(1,2),\ldots,(n-2,n-1),(n-1,0)\}</math> as the chess board. A permutation <math>\pi</math> which defines a way of seating the husbands, is a placement of <math>n</math> non-attacking rooks such that none of them is in <math>B</math>. | |||
{{Chess diagram small | |||
| | |||
| | |||
|= | |||
8 |xx|xx|__|__|__|__|__|__|= | |||
7 |__|xx|xx|__|__|__|__|__|= | |||
6 |__|__|xx|xx|__|__|__|__|= | |||
5 |__|__|__|xx|xx|__|__|__|= | |||
4 |__|__|__|__|xx|xx|__|__|= | |||
3 |__|__|__|__|__|xx|xx|__|= | |||
2 |__|__|__|__|__|__|xx|xx|= | |||
1 |xx|__|__|__|__|__|__|xx|= | |||
a b c d e f g h | |||
| | |||
}} | |||
We need to compute <math>r_k</math>, the number of ways of placing <math>k</math> non-attacking rooks on <math>B</math>. For our choice of <math>B</math>, <math>r_k</math> is the number of ways of choosing <math>k</math> points, no two consecutive, from a collection of <math>2n</math> points arranged in a circle. | |||
We first see how to do this in a ''line''. | |||
{{Theorem|Lemma| | |||
:The number of ways of choosing <math>k</math> ''non-consecutive'' objects from a collection of <math>m</math> objects arranged in a ''line'', is <math>{m-k+1\choose k}</math>. | |||
}} | |||
{{Proof| | |||
We draw a line of <math>m-k</math> black points, and then insert <math>k</math> red points into the <math>m-k+1</math> spaces between the black points (including the beginning and end). | |||
::<math> | |||
\begin{align} | |||
&\sqcup \, \bullet \, \sqcup \, \bullet \, \sqcup \, \bullet \, \sqcup \, \bullet \, \sqcup \, \bullet \, \sqcup \, \bullet \, \sqcup \, \bullet \, \sqcup \\ | |||
&\qquad\qquad\qquad\quad\Downarrow\\ | |||
&\sqcup \, \bullet \,\, {\color{Red}\bullet} \, \bullet \,\, {\color{Red}\bullet} \, \bullet \, \sqcup \, \bullet \,\, {\color{Red}\bullet}\, \, \bullet \, \sqcup \, \bullet \, \sqcup \, \bullet \,\, {\color{Red}\bullet} | |||
\end{align} | |||
</math> | |||
This gives us a line of <math>m</math> points, and the red points specifies the chosen objects, which are non-consecutive. The mapping is 1-1 correspondence. | |||
There are <math>{m-k+1\choose k}</math> ways of placing <math>k</math> red points into <math>m-k+1</math> spaces. | |||
}} | |||
The problem of choosing non-consecutive objects in a circle can be reduced to the case that the objects are in a line. | |||
{{Theorem|Lemma| | |||
:The number of ways of choosing <math>k</math> ''non-consecutive'' objects from a collection of <math>m</math> objects arranged in a ''circle'', is <math>\frac{m}{m-k}{m-k\choose k}</math>. | |||
}} | |||
{{Proof| | |||
Let <math>f(m,k)</math> be the desired number; and let <math>g(m,k)</math> be the number of ways of choosing <math>k</math> non-consecutive points from <math>m</math> points arranged in a circle, next coloring the <math>k</math> points red, and then coloring one of the uncolored point blue. | |||
Clearly, <math>g(m,k)=(m-k)f(m,k)</math>. | |||
But we can also compute <math>g(m,k)</math> as follows: | |||
* Choose one of the <math>m</math> points and color it blue. This gives us <math>m</math> ways. | |||
* Cut the circle to make a line of <math>m-1</math> points by removing the blue point. | |||
* Choose <math>k</math> non-consecutive points from the line of <math>m-1</math> points and color them red. This gives <math>{m-k\choose k}</math> ways due to the previous lemma. | |||
Thus, <math>g(m,k)=m{m-k\choose k}</math>. Therefore we have the desired number <math>f(m,k)=\frac{m}{m-k}{m-k\choose k}</math>. | |||
}} | |||
By the above lemma, we have that <math>r_k=\frac{2n}{2n-k}{2n-k\choose k}</math>. Then apply the theorem of counting permutations with restricted positions, | |||
:<math> | |||
N_0=\sum_{k=0}^n(-1)^kr_k(n-k)!=\sum_{k=0}^n(-1)^k\frac{2n}{2n-k}{2n-k\choose k}(n-k)!. | |||
</math> | |||
This gives the number of ways of seating the <math>n</math> husbands ''after the ladies are seated''. Recall that there are <math>2n!</math> ways of seating the <math>n</math> ladies. Thus, the total number of ways of seating <math>n</math> couples as required by problème des ménages is | |||
:<math> | |||
2n!\sum_{k=0}^n(-1)^k\frac{2n}{2n-k}{2n-k\choose k}(n-k)!. | |||
</math> | |||
=== The Euler totient function === | |||
Two integers <math>m, n</math> are said to be '''relatively prime''' if their greatest common diviser <math>\mathrm{gcd}(m,n)=1</math>. For a positive integer <math>n</math>, let <math>\phi(n)</math> be the number of positive integers from <math>\{1,2,\ldots,n\}</math> that are relative prime to <math>n</math>. This function, called the Euler <math>\phi</math> function or '''the Euler totient function''', is fundamental in number theory. | |||
We now derive a formula for this function by using the principle of inclusion-exclusion. | |||
{{Theorem|Theorem (The Euler totient function)| | |||
Suppose <math>n</math> is divisible by precisely <math>r</math> different primes, denoted <math>p_1,\ldots,p_r</math>. Then | |||
:<math>\phi(n)=n\prod_{i=1}^r\left(1-\frac{1}{p_i}\right)</math>. | |||
}} | |||
{{Proof| | |||
Let <math>U=\{1,2,\ldots,n\}</math> be the universe. The number of positive integers from <math>U</math> which is divisible by some <math>p_{i_1},p_{i_2},\ldots,p_{i_s}\in\{p_1,\ldots,p_r\}</math>, is <math>\frac{n}{p_{i_1}p_{i_2}\cdots p_{i_s}}</math>. | |||
<math>\phi(n)</math> is the number of integers from <math>U</math> which is not divisible by any <math>p_1,\ldots,p_r</math>. | |||
By principle of inclusion-exclusion, | |||
:<math> | |||
\begin{align} | |||
\phi(n) | |||
&=n+\sum_{k=1}^r(-1)^k\sum_{1\le i_1<i_2<\cdots <i_k\le n}\frac{n}{p_{i_1}p_{i_2}\cdots p_{i_k}}\\ | |||
&=n-\sum_{1\le i\le n}\frac{n}{p_i}+\sum_{1\le i<j\le n}\frac{n}{p_i p_j}-\sum_{1\le i<j<k\le n}\frac{n}{p_{i} p_{j} p_{k}}+\cdots + (-1)^r\frac{n}{p_{1}p_{2}\cdots p_{r}}\\ | |||
&=n\left(1-\sum_{1\le i\le n}\frac{1}{p_i}+\sum_{1\le i<j\le n}\frac{1}{p_i p_j}-\sum_{1\le i<j<k\le n}\frac{1}{p_{i} p_{j} p_{k}}+\cdots + (-1)^r\frac{1}{p_{1}p_{2}\cdots p_{r}}\right)\\ | |||
&=n\prod_{i=1}^n\left(1-\frac{1}{p_i}\right). | |||
\end{align} | |||
</math> | |||
}} | |||
== Möbius inversion == | |||
=== Posets === | |||
A '''partially ordered set''' or '''poset''' for short is a set <math>P</math> together with a binary relation denoted <math>\le_P</math> (or just <math>\le</math> if no confusion is caused), satisfying | |||
* (''reflexivity'') For all <math>x\in P, x\le x</math>. | |||
* (''antisymmetry'') If <math>x\le y</math> and <math>y\le x</math>, then <math>x=y</math>. | |||
* (''transitivity'') If <math>x\le y</math> and <math>y\le z</math>, then <math>x\le z</math>. | |||
We say two elements <math>x</math> and <math>y</math> are '''comparable''' if <math>x\le y</math> or <math>y\le x</math>; otherwise <math>x</math> and <math>y</math> are '''incomparable'''. | |||
;Notation | |||
* <math>x\ge y</math> means <math>y\le x</math>. | |||
* <math>x<y</math> means <math>x\le y</math> and <math>x\neq y</math>. | |||
* <math>x>y</math> means <math>y<x</math>. | |||
=== The Möbius function=== | |||
Let <math>P</math> be a finite poset. Consider functions in form of <math>\alpha:P\times P\rightarrow\mathbb{R}</math> defined over domain <math>P\times P</math>. It is convenient to treat such functions as matrices whose rows and columns are indexed by <math>P</math>. | |||
;Incidence algebra of poset | |||
:Let | |||
::<math>\mathbb{A}(P)=\{\alpha:P\times P\rightarrow\mathbb{R}\mid \alpha(x,y)=0\text{ for all }x\not\le_P y\}</math> | |||
:be the class of <math>\alpha</math> such that <math>\alpha(x,y)</math> is non-zero only for <math>x\le_P y</math>. | |||
:Treating <math>\alpha</math> as matrix, it is trivial to see that <math>\mathbb{A}(P)</math> is closed under addition and scalar multiplication, that is, | |||
:* if <math>\alpha,\beta\in \mathbb{A}(P)</math> then <math>\alpha+\beta\in\mathbb{A}(P)</math>; | |||
:* if <math>\alpha\in \mathbb{A}(P)</math> then <math>c\alpha\in\mathbb{A}(P)</math> for any <math>c\in\mathbb{R}</math>; | |||
:where <math>\alpha,\beta</math> are treated as matrices. | |||
:With this spirit, it is natural to define the matrix multiplication in <math>\mathbb{A}(P)</math>. For <math>\alpha,\beta\in \mathbb{A}(P)</math>, | |||
::<math>(\alpha\beta)(x,y)=\sum_{z\in P}\alpha(x,z)\beta(z,y)=\sum_{x\le z\le y}\alpha(x,z)\beta(z,y)</math>. | |||
:The second equation is due to that for <math>\alpha,\beta\in \mathbb{A}(P)</math>, for all <math>z</math> other than <math>x\le z\le y</math>, <math>\alpha(x,z)\beta(z,y)</math> is zero. | |||
:By transitivity, it is also easy to observe that <math>\mathbb{A}(P)</math> is closed under matrix multiplication (the detailed proof is left as an exercise). Therefore, <math>\mathbb{A}(P)</math> is closed under addition, scalar multiplication and matrix multiplication, so we have an algebra <math>\mathbb{A}(P)</math>, called '''incidence algebra''', over functions on <math>P\times P</math>. | |||
;Zeta function and Möbius function | |||
:A special function in <math>\mathbb{A}(P)</math> is the so-called '''zeta function''' <math>\zeta</math>, defined as | |||
::<math>\zeta(x,y)=\begin{cases}1&\text{if }x\le_P y,\\0 &\text{otherwise.}\end{cases}</math> | |||
:As a matrix (or more accurately, as an element of the incidence algebra), <math>\zeta</math> is invertible and its inversion, denoted by <math>\mu</math>, is called the '''Möbius function'''. More precisely, <math>\mu</math> is also in the incidence algebra <math>\mathbb{A}(P)</math>, and <math>\mu\zeta=I</math> where <math>I</math> is the identity matrix (the identity of the incidence algebra <math>\mathbb{A}(P)</math>). | |||
There is an equivalent explicit definition of Möbius function. | |||
{{Theorem|Definition (Möbius function)| | |||
:<math>\mu(x,y)=\begin{cases} | |||
-\sum_{x\le z\le y}\mu(x,z)&\text{if }x<y,\\ | |||
1&\text{if }x=y,\\ | |||
0&\text{if }x\not\le y. | |||
\end{cases} | |||
</math> | |||
}} | |||
To see the equivalence between this definition and the inversion of zeta function, we may have the following proposition, which is proved by directly evaluating <math>\mu\zeta</math>. | |||
{{Theorem|Proposition| | |||
:For any <math>x,y\in P</math>, | |||
::<math>\sum_{x\le z\le y}\mu(x,z)=\begin{cases}1 &\text{if }x=y,\\ | |||
0 &\text{otherwise.}\end{cases}</math> | |||
}} | |||
{{Proof| | |||
It holds that | |||
:<math>(\mu\zeta)(x,y)=\sum_{x\le z\le y}\mu(x,z)\zeta(z,y)=\sum_{x\le z\le y}\mu(x,z)</math>. | |||
On the other hand, <math>\mu\zeta=I</math>, i.e. | |||
:<math>(\mu\zeta)(x,y)=\begin{cases}1 &\text{if }x=y,\\ | |||
0 &\text{otherwise.}\end{cases}</math> | |||
The proposition follows. | |||
}} | |||
Note that <math>\mu(x,y)=\sum_{x\le z\le y}\mu(x,z)-\sum_{x\le z< y}\mu(x,z)</math>, which gives the above inductive definition of Möbius function. | |||
=== Principle of Möbius inversion === | |||
{{Theorem|Möbius inversion formula| | |||
:Let <math>P</math> be a finite poset and <math>\mu</math> its Möbius function. Let <math>f,g:P\rightarrow \mathbb{R}</math>. Then | |||
::<math>\forall x\in P,\,\, g(x)=\sum_{y\le x} f(y)</math>, | |||
:if and only if | |||
::<math>\forall x\in P,\,\, f(x)=\sum_{y\le x}g(y)\mu(y,x)</math>. | |||
}} | |||
{{Theorem|Möbius inversion formula, dual form| | |||
:Let <math>P</math> be a finite poset and <math>\mu</math> its Möbius function. Let <math>f,g:P\rightarrow \mathbb{R}</math>. Then | |||
::<math>\forall x\in P, \,\, g(x)=\sum_{y{\color{red}\ge} x} f(y)</math>, | |||
: if and only if | |||
::<math>\forall x\in P, \,\, f(x)=\sum_{y{\color{red}\ge} x}g(y)\mu(y,x)</math>. | |||
}} | |||
= | == Reference == | ||
* | * ''Stanley,'' Enumerative Combinatorics, Volume 1, Chapter 2. | ||
* ''van Lin and Wilson'', A course in combinatorics, Chapter 10, 15. | |||
* | |||
Revision as of 09:08, 21 September 2011
Principle of Inclusion-Exclusion
Let [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] be two finite sets. The cardinality of their union is
- [math]\displaystyle{ |A\cup B|=|A|+|B|-{\color{Blue}|A\cap B|} }[/math].
For three sets [math]\displaystyle{ A }[/math], [math]\displaystyle{ B }[/math], and [math]\displaystyle{ C }[/math], the cardinality of the union of these three sets is computed as
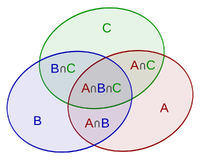
- [math]\displaystyle{ |A\cup B\cup C|=|A|+|B|+|C|-{\color{Blue}|A\cap B|}-{\color{Blue}|A\cap C|}-{\color{Blue}|B\cap C|}+{\color{Red}|A\cap B\cap C|} }[/math].
This is illustrated by the following figure.
Generally, the Principle of Inclusion-Exclusion states the rule for computing the union of [math]\displaystyle{ n }[/math] finite sets [math]\displaystyle{ A_1,A_2,\ldots,A_n }[/math], such that
[math]\displaystyle{ \begin{align} \left|\bigcup_{i=1}^nA_i\right| &= \sum_{I\subseteq\{1,\ldots,n\}}(-1)^{|I|-1}\left|\bigcap_{i\in I}A_i\right|. \end{align} }[/math]
In combinatorial enumeration, the Principle of Inclusion-Exclusion is usually applied in its complement form.
Let [math]\displaystyle{ A_1,A_2,\ldots,A_n\subseteq U }[/math] be subsets of some finite set [math]\displaystyle{ U }[/math]. Here [math]\displaystyle{ U }[/math] is some universe of combinatorial objects, whose cardinality is easy to calculate (e.g. all strings, tuples, permutations), and each [math]\displaystyle{ A_i }[/math] contains the objects with some specific property (e.g. a "pattern") which we want to avoid. The problem is to count the number of objects without any of the [math]\displaystyle{ n }[/math] properties. We write [math]\displaystyle{ \bar{A_i}=U-A_i }[/math]. The number of objects without any of the properties [math]\displaystyle{ A_1,A_2,\ldots,A_n }[/math] is
[math]\displaystyle{ \begin{align} \left|\bar{A_1}\cap\bar{A_2}\cap\cdots\cap\bar{A_n}\right|=\left|U-\bigcup_{i=1}^nA_i\right| &= |U|+\sum_{I\subseteq\{1,\ldots,n\}}(-1)^{|I|}\left|\bigcap_{i\in I}A_i\right|. \end{align} }[/math]
For an [math]\displaystyle{ I\subseteq\{1,2,\ldots,n\} }[/math], we denote
- [math]\displaystyle{ A_I=\bigcap_{i\in I}A_i }[/math]
with the convention that [math]\displaystyle{ A_\emptyset=U }[/math]. The above equation is stated as:
Principle of Inclusion-Exclusion - Let [math]\displaystyle{ A_1,A_2,\ldots,A_n }[/math] be a family of subsets of [math]\displaystyle{ U }[/math]. Then the number of elements of [math]\displaystyle{ U }[/math] which lie in none of the subsets [math]\displaystyle{ A_i }[/math] is
- [math]\displaystyle{ \sum_{I\subseteq\{1,\ldots, n\}}(-1)^{|I|}|A_I| }[/math].
- Let [math]\displaystyle{ A_1,A_2,\ldots,A_n }[/math] be a family of subsets of [math]\displaystyle{ U }[/math]. Then the number of elements of [math]\displaystyle{ U }[/math] which lie in none of the subsets [math]\displaystyle{ A_i }[/math] is
Let [math]\displaystyle{ S_k=\sum_{|I|=k}|A_I|\, }[/math]. Conventionally, [math]\displaystyle{ S_0=|A_\emptyset|=|U| }[/math]. The principle of inclusion-exclusion can be expressed as
Surjections
In the twelvefold way, we discuss the counting problems incurred by the mappings [math]\displaystyle{ f:N\rightarrow M }[/math]. The basic case is that elements from both [math]\displaystyle{ N }[/math] and [math]\displaystyle{ M }[/math] are distinguishable. In this case, it is easy to count the number of arbitrary mappings (which is [math]\displaystyle{ m^n }[/math]) and the number of injective (one-to-one) mappings (which is [math]\displaystyle{ (m)_n }[/math]), but the number of surjective is difficult. Here we apply the principle of inclusion-exclusion to count the number of surjective (onto) mappings.
Theorem - The number of surjective mappings from an [math]\displaystyle{ n }[/math]-set to an [math]\displaystyle{ m }[/math]-set is given by
- [math]\displaystyle{ \sum_{k=1}^m(-1)^{m-k}{m\choose k}k^n }[/math].
- The number of surjective mappings from an [math]\displaystyle{ n }[/math]-set to an [math]\displaystyle{ m }[/math]-set is given by
Proof. Let [math]\displaystyle{ U=\{f:[n]\rightarrow[m]\} }[/math] be the set of mappings from [math]\displaystyle{ [n] }[/math] to [math]\displaystyle{ [m] }[/math]. Then [math]\displaystyle{ |U|=m^n }[/math].
For [math]\displaystyle{ i\in[m] }[/math], let [math]\displaystyle{ A_i }[/math] be the set of mappings [math]\displaystyle{ f:[n]\rightarrow[m] }[/math] that none of [math]\displaystyle{ j\in[n] }[/math] is mapped to [math]\displaystyle{ i }[/math], i.e. [math]\displaystyle{ A_i=\{f:[n]\rightarrow[m]\setminus\{i\}\} }[/math], thus [math]\displaystyle{ |A_i|=(m-1)^n }[/math].
More generally, for [math]\displaystyle{ I\subseteq [m] }[/math], [math]\displaystyle{ A_I=\bigcap_{i\in I}A_i }[/math] contains the mappings [math]\displaystyle{ f:[n]\rightarrow[m]\setminus I }[/math]. And [math]\displaystyle{ |A_I|=(m-|I|)^n\, }[/math].
A mapping [math]\displaystyle{ f:[n]\rightarrow[m] }[/math] is surjective if [math]\displaystyle{ f }[/math] lies in none of [math]\displaystyle{ A_i }[/math]. By the principle of inclusion-exclusion, the number of surjective [math]\displaystyle{ f:[n]\rightarrow[m] }[/math] is
- [math]\displaystyle{ \sum_{I\subseteq[m]}(-1)^{|I|}\left|A_I\right|=\sum_{I\subseteq[m]}(-1)^{|I|}(m-|I|)^n=\sum_{j=0}^m(-1)^j{m\choose j}(m-j)^n }[/math].
Let [math]\displaystyle{ k=m-j }[/math]. The theorem is proved.
- [math]\displaystyle{ \square }[/math]
Recall that, in the twelvefold way, we establish a relation between surjections and partitions.
- Surjection to ordered partition:
- For a surjective [math]\displaystyle{ f:[n]\rightarrow[m] }[/math], [math]\displaystyle{ (f^{-1}(0),f^{-1}(1),\ldots,f^{-1}(m-1)) }[/math] is an ordered partition of [math]\displaystyle{ [n] }[/math].
- Ordered partition to surjection:
- For an ordered [math]\displaystyle{ m }[/math]-partition [math]\displaystyle{ (B_0,B_1,\ldots, B_{m-1}) }[/math] of [math]\displaystyle{ [n] }[/math], we can define a function [math]\displaystyle{ f:[n]\rightarrow[m] }[/math] by letting [math]\displaystyle{ f(i)=j }[/math] if and only if [math]\displaystyle{ i\in B_j }[/math]. [math]\displaystyle{ f }[/math] is surjective since as a partition, none of [math]\displaystyle{ B_i }[/math] is empty.
Therefore, we have a one-to-one correspondence between surjective mappings from an [math]\displaystyle{ n }[/math]-set to an [math]\displaystyle{ m }[/math]-set and the ordered [math]\displaystyle{ m }[/math]-partitions of an [math]\displaystyle{ n }[/math]-set.
The Stirling number of the second kind [math]\displaystyle{ S(n,m) }[/math] is the number of [math]\displaystyle{ m }[/math]-partitions of an [math]\displaystyle{ n }[/math]-set. There are [math]\displaystyle{ m! }[/math] ways to order an [math]\displaystyle{ m }[/math]-partition, thus the number of surjective mappings [math]\displaystyle{ f:[n]\rightarrow[m] }[/math] is [math]\displaystyle{ m! S(n,m) }[/math]. Combining with what we have proved for surjections, we give the following result for the Stirling number of the second kind.
Proposition - [math]\displaystyle{ S(n,m)=\frac{1}{m!}\sum_{k=1}^m(-1)^{m-k}{m\choose k}k^n }[/math].
Derangements
We now count the number of bijections from a set to itself with no fixed points. This is the derangement problem.
For a permutation [math]\displaystyle{ \pi }[/math] of [math]\displaystyle{ \{1,2,\ldots,n\} }[/math], a fixed point is such an [math]\displaystyle{ i\in\{1,2,\ldots,n\} }[/math] that [math]\displaystyle{ \pi(i)=i }[/math]. A derangement of [math]\displaystyle{ \{1,2,\ldots,n\} }[/math] is a permutation of [math]\displaystyle{ \{1,2,\ldots,n\} }[/math] that has no fixed points.
Theorem - The number of derangements of [math]\displaystyle{ \{1,2,\ldots,n\} }[/math] given by
- [math]\displaystyle{ n!\sum_{k=0}^n\frac{(-1)^k}{k!}\approx \frac{n!}{\mathrm{e}} }[/math].
- The number of derangements of [math]\displaystyle{ \{1,2,\ldots,n\} }[/math] given by
Proof. Let [math]\displaystyle{ U }[/math] be the set of all permutations of [math]\displaystyle{ \{1,2,\ldots,n\} }[/math]. So [math]\displaystyle{ |U|=n! }[/math].
Let [math]\displaystyle{ A_i }[/math] be the set of permutations with fixed point [math]\displaystyle{ i }[/math]; so [math]\displaystyle{ |A_i|=(n-1)! }[/math]. More generally, for any [math]\displaystyle{ I\subseteq \{1,2,\ldots,n\} }[/math], [math]\displaystyle{ A_I=\bigcap_{i\in I}A_i }[/math], and [math]\displaystyle{ |A_I|=(n-|I|)! }[/math], since permutations in [math]\displaystyle{ A_I }[/math] fix every point in [math]\displaystyle{ I }[/math] and permute the remaining points arbitrarily. A permutation is a derangement if and only if it lies in none of the sets [math]\displaystyle{ A_i }[/math]. So the number of derangements is
- [math]\displaystyle{ \sum_{I\subseteq\{1,2,\ldots,n\}}(-1)^{|I|}(n-|I|)!=\sum_{k=0}^n(-1)^k{n\choose k}(n-k)!=n!\sum_{k=0}^n\frac{(-1)^k}{k!}. }[/math]
By Taylor's series,
- [math]\displaystyle{ \frac{1}{\mathrm{e}}=\sum_{k=0}^\infty\frac{(-1)^k}{k!}=\sum_{k=0}^n\frac{(-1)^k}{k!}\pm o\left(\frac{1}{n!}\right) }[/math].
It is not hard to see that [math]\displaystyle{ n!\sum_{k=0}^n\frac{(-1)^k}{k!} }[/math] is the closest integer to [math]\displaystyle{ \frac{n!}{\mathrm{e}} }[/math].
- [math]\displaystyle{ \square }[/math]
Therefore, there are about [math]\displaystyle{ \frac{1}{\mathrm{e}} }[/math] fraction of all permutations with no fixed points.
Permutations with restricted positions
We introduce a general theory of counting permutations with restricted positions. In the derangement problem, we count the number of permutations that [math]\displaystyle{ \pi(i)\neq i }[/math]. We now generalize to the problem of counting permutations which avoid a set of arbitrarily specified positions.
It is traditionally described using terminology from the game of chess. Let [math]\displaystyle{ B\subseteq \{1,\ldots,n\}\times \{1,\ldots,n\} }[/math], called a board. As illustrated below, we can think of [math]\displaystyle{ B }[/math] as a chess board, with the positions in [math]\displaystyle{ B }[/math] marked by "[math]\displaystyle{ \times }[/math]".
For a permutation [math]\displaystyle{ \pi }[/math] of [math]\displaystyle{ \{1,\ldots,n\} }[/math], define the graph [math]\displaystyle{ G_\pi(V,E) }[/math] as
- [math]\displaystyle{ \begin{align} G_\pi &= \{(i,\pi(i))\mid i\in \{1,2,\ldots,n\}\}. \end{align} }[/math]
This can also be viewed as a set of marked positions on a chess board. Each row and each column has only one marked position, because [math]\displaystyle{ \pi }[/math] is a permutation. Thus, we can identify each [math]\displaystyle{ G_\pi }[/math] as a placement of [math]\displaystyle{ n }[/math] rooks (“城堡”,规则同中国象棋里的“车”) without attacking each other.
For example, the following is the [math]\displaystyle{ G_\pi }[/math] of such [math]\displaystyle{ \pi }[/math] that [math]\displaystyle{ \pi(i)=i }[/math].
Now define
- [math]\displaystyle{ \begin{align} N_0 &= \left|\left\{\pi\mid B\cap G_\pi=\emptyset\right\}\right|\\ r_k &= \mbox{number of }k\mbox{-subsets of }B\mbox{ such that no two elements have a common coordinate}\\ &=\left|\left\{S\in{B\choose k} \,\bigg|\, \forall (i_1,j_1),(i_2,j_2)\in S, i_1\neq i_2, j_1\neq j_2 \right\}\right| \end{align} }[/math]
Interpreted in chess game,
- [math]\displaystyle{ B }[/math]: a set of marked positions in an [math]\displaystyle{ [n]\times [n] }[/math] chess board.
- [math]\displaystyle{ N_0 }[/math]: the number of ways of placing [math]\displaystyle{ n }[/math] non-attacking rooks on the chess board such that none of these rooks lie in [math]\displaystyle{ B }[/math].
- [math]\displaystyle{ r_k }[/math]: number of ways of placing [math]\displaystyle{ k }[/math] non-attacking rooks on [math]\displaystyle{ B }[/math].
Our goal is to count [math]\displaystyle{ N_0 }[/math] in terms of [math]\displaystyle{ r_k }[/math]. This gives the number of permutations avoid all positions in a [math]\displaystyle{ B }[/math].
Theorem - [math]\displaystyle{ N_0=\sum_{k=0}^n(-1)^kr_k(n-k)! }[/math].
Proof. For each [math]\displaystyle{ i\in[n] }[/math], let [math]\displaystyle{ A_i=\{\pi\mid (i,\pi(i))\in B\} }[/math] be the set of permutations [math]\displaystyle{ \pi }[/math] whose [math]\displaystyle{ i }[/math]-th position is in [math]\displaystyle{ B }[/math].
[math]\displaystyle{ N_0 }[/math] is the number of permutations avoid all positions in [math]\displaystyle{ B }[/math]. Thus, our goal is to count the number of permutations [math]\displaystyle{ \pi }[/math] in none of [math]\displaystyle{ A_i }[/math] for [math]\displaystyle{ i\in [n] }[/math].
For each [math]\displaystyle{ I\subseteq [n] }[/math], let [math]\displaystyle{ A_I=\bigcap_{i\in I}A_i }[/math], which is the set of permutations [math]\displaystyle{ \pi }[/math] such that [math]\displaystyle{ (i,\pi(i))\in B }[/math] for all [math]\displaystyle{ i\in I }[/math]. Due to the principle of inclusion-exclusion,
- [math]\displaystyle{ N_0=\sum_{I\subseteq [n]} (-1)^{|I|}|A_I|=\sum_{k=0}^n(-1)^k\sum_{I\in{[n]\choose k}}|A_I| }[/math].
The next observation is that
- [math]\displaystyle{ \sum_{I\in{[n]\choose k}}|A_I|=r_k(n-k)! }[/math],
because we can count both sides by first placing [math]\displaystyle{ k }[/math] non-attacking rooks on [math]\displaystyle{ B }[/math] and placing [math]\displaystyle{ n-k }[/math] additional non-attacking rooks on [math]\displaystyle{ [n]\times [n] }[/math] in [math]\displaystyle{ (n-k)! }[/math] ways.
Therefore,
- [math]\displaystyle{ N_0=\sum_{k=0}^n(-1)^kr_k(n-k)! }[/math].
- [math]\displaystyle{ \square }[/math]
Derangement problem
We use the above general method to solve the derange problem again.
Take [math]\displaystyle{ B=\{(1,1),(2,2),\ldots,(n,n)\} }[/math] as the chess board. A derangement [math]\displaystyle{ \pi }[/math] is a placement of [math]\displaystyle{ n }[/math] non-attacking rooks such that none of them is in [math]\displaystyle{ B }[/math].
Clearly, the number of ways of placing [math]\displaystyle{ k }[/math] non-attacking rooks on [math]\displaystyle{ B }[/math] is [math]\displaystyle{ r_k={n\choose k} }[/math]. We want to count [math]\displaystyle{ N_0 }[/math], which gives the number of ways of placing [math]\displaystyle{ n }[/math] non-attacking rooks such that none of these rooks lie in [math]\displaystyle{ B }[/math].
By the above theorem
- [math]\displaystyle{ N_0=\sum_{k=0}^n(-1)^kr_k(n-k)!=\sum_{k=0}^n(-1)^k{n\choose k}(n-k)!=\sum_{k=0}^n(-1)^k\frac{n!}{k!}=n!\sum_{k=0}^n(-1)^k\frac{1}{k!}\approx\frac{n!}{e}. }[/math]
Problème des ménages
Suppose that in a banquet, we want to seat [math]\displaystyle{ n }[/math] couples at a circular table, satisfying the following constraints:
- Men and women are in alternate places.
- No one sits next to his/her spouse.
In how many ways can this be done?
(For convenience, we assume that every seat at the table marked differently so that rotating the seats clockwise or anti-clockwise will end up with a different solution.)
First, let the [math]\displaystyle{ n }[/math] ladies find their seats. They may either sit at the odd numbered seats or even numbered seats, in either case, there are [math]\displaystyle{ n! }[/math] different orders. Thus, there are [math]\displaystyle{ 2(n!) }[/math] ways to seat the [math]\displaystyle{ n }[/math] ladies.
After sitting the wives, we label the remaining [math]\displaystyle{ n }[/math] places clockwise as [math]\displaystyle{ 0,1,\ldots, n-1 }[/math]. And a seating of the [math]\displaystyle{ n }[/math] husbands is given by a permutation [math]\displaystyle{ \pi }[/math] of [math]\displaystyle{ [n] }[/math] defined as follows. Let [math]\displaystyle{ \pi(i) }[/math] be the seat of the husband of he lady sitting at the [math]\displaystyle{ i }[/math]-th place.
It is easy to see that [math]\displaystyle{ \pi }[/math] satisfies that [math]\displaystyle{ \pi(i)\neq i }[/math] and [math]\displaystyle{ \pi(i)\not\equiv i+1\pmod n }[/math], and every permutation [math]\displaystyle{ \pi }[/math] with these properties gives a feasible seating of the [math]\displaystyle{ n }[/math] husbands. Thus, we only need to count the number of permutations [math]\displaystyle{ \pi }[/math] such that [math]\displaystyle{ \pi(i)\not\equiv i, i+1\pmod n }[/math].
Take [math]\displaystyle{ B=\{(0,0),(1,1),\ldots,(n-1,n-1), (0,1),(1,2),\ldots,(n-2,n-1),(n-1,0)\} }[/math] as the chess board. A permutation [math]\displaystyle{ \pi }[/math] which defines a way of seating the husbands, is a placement of [math]\displaystyle{ n }[/math] non-attacking rooks such that none of them is in [math]\displaystyle{ B }[/math].
We need to compute [math]\displaystyle{ r_k }[/math], the number of ways of placing [math]\displaystyle{ k }[/math] non-attacking rooks on [math]\displaystyle{ B }[/math]. For our choice of [math]\displaystyle{ B }[/math], [math]\displaystyle{ r_k }[/math] is the number of ways of choosing [math]\displaystyle{ k }[/math] points, no two consecutive, from a collection of [math]\displaystyle{ 2n }[/math] points arranged in a circle.
We first see how to do this in a line.
Lemma - The number of ways of choosing [math]\displaystyle{ k }[/math] non-consecutive objects from a collection of [math]\displaystyle{ m }[/math] objects arranged in a line, is [math]\displaystyle{ {m-k+1\choose k} }[/math].
Proof. We draw a line of [math]\displaystyle{ m-k }[/math] black points, and then insert [math]\displaystyle{ k }[/math] red points into the [math]\displaystyle{ m-k+1 }[/math] spaces between the black points (including the beginning and end).
- [math]\displaystyle{ \begin{align} &\sqcup \, \bullet \, \sqcup \, \bullet \, \sqcup \, \bullet \, \sqcup \, \bullet \, \sqcup \, \bullet \, \sqcup \, \bullet \, \sqcup \, \bullet \, \sqcup \\ &\qquad\qquad\qquad\quad\Downarrow\\ &\sqcup \, \bullet \,\, {\color{Red}\bullet} \, \bullet \,\, {\color{Red}\bullet} \, \bullet \, \sqcup \, \bullet \,\, {\color{Red}\bullet}\, \, \bullet \, \sqcup \, \bullet \, \sqcup \, \bullet \,\, {\color{Red}\bullet} \end{align} }[/math]
This gives us a line of [math]\displaystyle{ m }[/math] points, and the red points specifies the chosen objects, which are non-consecutive. The mapping is 1-1 correspondence. There are [math]\displaystyle{ {m-k+1\choose k} }[/math] ways of placing [math]\displaystyle{ k }[/math] red points into [math]\displaystyle{ m-k+1 }[/math] spaces.
- [math]\displaystyle{ \square }[/math]
The problem of choosing non-consecutive objects in a circle can be reduced to the case that the objects are in a line.
Lemma - The number of ways of choosing [math]\displaystyle{ k }[/math] non-consecutive objects from a collection of [math]\displaystyle{ m }[/math] objects arranged in a circle, is [math]\displaystyle{ \frac{m}{m-k}{m-k\choose k} }[/math].
Proof. Let [math]\displaystyle{ f(m,k) }[/math] be the desired number; and let [math]\displaystyle{ g(m,k) }[/math] be the number of ways of choosing [math]\displaystyle{ k }[/math] non-consecutive points from [math]\displaystyle{ m }[/math] points arranged in a circle, next coloring the [math]\displaystyle{ k }[/math] points red, and then coloring one of the uncolored point blue.
Clearly, [math]\displaystyle{ g(m,k)=(m-k)f(m,k) }[/math].
But we can also compute [math]\displaystyle{ g(m,k) }[/math] as follows:
- Choose one of the [math]\displaystyle{ m }[/math] points and color it blue. This gives us [math]\displaystyle{ m }[/math] ways.
- Cut the circle to make a line of [math]\displaystyle{ m-1 }[/math] points by removing the blue point.
- Choose [math]\displaystyle{ k }[/math] non-consecutive points from the line of [math]\displaystyle{ m-1 }[/math] points and color them red. This gives [math]\displaystyle{ {m-k\choose k} }[/math] ways due to the previous lemma.
Thus, [math]\displaystyle{ g(m,k)=m{m-k\choose k} }[/math]. Therefore we have the desired number [math]\displaystyle{ f(m,k)=\frac{m}{m-k}{m-k\choose k} }[/math].
- [math]\displaystyle{ \square }[/math]
By the above lemma, we have that [math]\displaystyle{ r_k=\frac{2n}{2n-k}{2n-k\choose k} }[/math]. Then apply the theorem of counting permutations with restricted positions,
- [math]\displaystyle{ N_0=\sum_{k=0}^n(-1)^kr_k(n-k)!=\sum_{k=0}^n(-1)^k\frac{2n}{2n-k}{2n-k\choose k}(n-k)!. }[/math]
This gives the number of ways of seating the [math]\displaystyle{ n }[/math] husbands after the ladies are seated. Recall that there are [math]\displaystyle{ 2n! }[/math] ways of seating the [math]\displaystyle{ n }[/math] ladies. Thus, the total number of ways of seating [math]\displaystyle{ n }[/math] couples as required by problème des ménages is
- [math]\displaystyle{ 2n!\sum_{k=0}^n(-1)^k\frac{2n}{2n-k}{2n-k\choose k}(n-k)!. }[/math]
The Euler totient function
Two integers [math]\displaystyle{ m, n }[/math] are said to be relatively prime if their greatest common diviser [math]\displaystyle{ \mathrm{gcd}(m,n)=1 }[/math]. For a positive integer [math]\displaystyle{ n }[/math], let [math]\displaystyle{ \phi(n) }[/math] be the number of positive integers from [math]\displaystyle{ \{1,2,\ldots,n\} }[/math] that are relative prime to [math]\displaystyle{ n }[/math]. This function, called the Euler [math]\displaystyle{ \phi }[/math] function or the Euler totient function, is fundamental in number theory.
We now derive a formula for this function by using the principle of inclusion-exclusion.
Theorem (The Euler totient function) Suppose [math]\displaystyle{ n }[/math] is divisible by precisely [math]\displaystyle{ r }[/math] different primes, denoted [math]\displaystyle{ p_1,\ldots,p_r }[/math]. Then
- [math]\displaystyle{ \phi(n)=n\prod_{i=1}^r\left(1-\frac{1}{p_i}\right) }[/math].
Proof. Let [math]\displaystyle{ U=\{1,2,\ldots,n\} }[/math] be the universe. The number of positive integers from [math]\displaystyle{ U }[/math] which is divisible by some [math]\displaystyle{ p_{i_1},p_{i_2},\ldots,p_{i_s}\in\{p_1,\ldots,p_r\} }[/math], is [math]\displaystyle{ \frac{n}{p_{i_1}p_{i_2}\cdots p_{i_s}} }[/math].
[math]\displaystyle{ \phi(n) }[/math] is the number of integers from [math]\displaystyle{ U }[/math] which is not divisible by any [math]\displaystyle{ p_1,\ldots,p_r }[/math]. By principle of inclusion-exclusion,
- [math]\displaystyle{ \begin{align} \phi(n) &=n+\sum_{k=1}^r(-1)^k\sum_{1\le i_1\lt i_2\lt \cdots \lt i_k\le n}\frac{n}{p_{i_1}p_{i_2}\cdots p_{i_k}}\\ &=n-\sum_{1\le i\le n}\frac{n}{p_i}+\sum_{1\le i\lt j\le n}\frac{n}{p_i p_j}-\sum_{1\le i\lt j\lt k\le n}\frac{n}{p_{i} p_{j} p_{k}}+\cdots + (-1)^r\frac{n}{p_{1}p_{2}\cdots p_{r}}\\ &=n\left(1-\sum_{1\le i\le n}\frac{1}{p_i}+\sum_{1\le i\lt j\le n}\frac{1}{p_i p_j}-\sum_{1\le i\lt j\lt k\le n}\frac{1}{p_{i} p_{j} p_{k}}+\cdots + (-1)^r\frac{1}{p_{1}p_{2}\cdots p_{r}}\right)\\ &=n\prod_{i=1}^n\left(1-\frac{1}{p_i}\right). \end{align} }[/math]
- [math]\displaystyle{ \square }[/math]
Möbius inversion
Posets
A partially ordered set or poset for short is a set [math]\displaystyle{ P }[/math] together with a binary relation denoted [math]\displaystyle{ \le_P }[/math] (or just [math]\displaystyle{ \le }[/math] if no confusion is caused), satisfying
- (reflexivity) For all [math]\displaystyle{ x\in P, x\le x }[/math].
- (antisymmetry) If [math]\displaystyle{ x\le y }[/math] and [math]\displaystyle{ y\le x }[/math], then [math]\displaystyle{ x=y }[/math].
- (transitivity) If [math]\displaystyle{ x\le y }[/math] and [math]\displaystyle{ y\le z }[/math], then [math]\displaystyle{ x\le z }[/math].
We say two elements [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] are comparable if [math]\displaystyle{ x\le y }[/math] or [math]\displaystyle{ y\le x }[/math]; otherwise [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] are incomparable.
- Notation
- [math]\displaystyle{ x\ge y }[/math] means [math]\displaystyle{ y\le x }[/math].
- [math]\displaystyle{ x\lt y }[/math] means [math]\displaystyle{ x\le y }[/math] and [math]\displaystyle{ x\neq y }[/math].
- [math]\displaystyle{ x\gt y }[/math] means [math]\displaystyle{ y\lt x }[/math].
The Möbius function
Let [math]\displaystyle{ P }[/math] be a finite poset. Consider functions in form of [math]\displaystyle{ \alpha:P\times P\rightarrow\mathbb{R} }[/math] defined over domain [math]\displaystyle{ P\times P }[/math]. It is convenient to treat such functions as matrices whose rows and columns are indexed by [math]\displaystyle{ P }[/math].
- Incidence algebra of poset
- Let
- [math]\displaystyle{ \mathbb{A}(P)=\{\alpha:P\times P\rightarrow\mathbb{R}\mid \alpha(x,y)=0\text{ for all }x\not\le_P y\} }[/math]
- be the class of [math]\displaystyle{ \alpha }[/math] such that [math]\displaystyle{ \alpha(x,y) }[/math] is non-zero only for [math]\displaystyle{ x\le_P y }[/math].
- Treating [math]\displaystyle{ \alpha }[/math] as matrix, it is trivial to see that [math]\displaystyle{ \mathbb{A}(P) }[/math] is closed under addition and scalar multiplication, that is,
- if [math]\displaystyle{ \alpha,\beta\in \mathbb{A}(P) }[/math] then [math]\displaystyle{ \alpha+\beta\in\mathbb{A}(P) }[/math];
- if [math]\displaystyle{ \alpha\in \mathbb{A}(P) }[/math] then [math]\displaystyle{ c\alpha\in\mathbb{A}(P) }[/math] for any [math]\displaystyle{ c\in\mathbb{R} }[/math];
- where [math]\displaystyle{ \alpha,\beta }[/math] are treated as matrices.
- With this spirit, it is natural to define the matrix multiplication in [math]\displaystyle{ \mathbb{A}(P) }[/math]. For [math]\displaystyle{ \alpha,\beta\in \mathbb{A}(P) }[/math],
- [math]\displaystyle{ (\alpha\beta)(x,y)=\sum_{z\in P}\alpha(x,z)\beta(z,y)=\sum_{x\le z\le y}\alpha(x,z)\beta(z,y) }[/math].
- The second equation is due to that for [math]\displaystyle{ \alpha,\beta\in \mathbb{A}(P) }[/math], for all [math]\displaystyle{ z }[/math] other than [math]\displaystyle{ x\le z\le y }[/math], [math]\displaystyle{ \alpha(x,z)\beta(z,y) }[/math] is zero.
- By transitivity, it is also easy to observe that [math]\displaystyle{ \mathbb{A}(P) }[/math] is closed under matrix multiplication (the detailed proof is left as an exercise). Therefore, [math]\displaystyle{ \mathbb{A}(P) }[/math] is closed under addition, scalar multiplication and matrix multiplication, so we have an algebra [math]\displaystyle{ \mathbb{A}(P) }[/math], called incidence algebra, over functions on [math]\displaystyle{ P\times P }[/math].
- Zeta function and Möbius function
- A special function in [math]\displaystyle{ \mathbb{A}(P) }[/math] is the so-called zeta function [math]\displaystyle{ \zeta }[/math], defined as
- [math]\displaystyle{ \zeta(x,y)=\begin{cases}1&\text{if }x\le_P y,\\0 &\text{otherwise.}\end{cases} }[/math]
- As a matrix (or more accurately, as an element of the incidence algebra), [math]\displaystyle{ \zeta }[/math] is invertible and its inversion, denoted by [math]\displaystyle{ \mu }[/math], is called the Möbius function. More precisely, [math]\displaystyle{ \mu }[/math] is also in the incidence algebra [math]\displaystyle{ \mathbb{A}(P) }[/math], and [math]\displaystyle{ \mu\zeta=I }[/math] where [math]\displaystyle{ I }[/math] is the identity matrix (the identity of the incidence algebra [math]\displaystyle{ \mathbb{A}(P) }[/math]).
There is an equivalent explicit definition of Möbius function.
Definition (Möbius function) - [math]\displaystyle{ \mu(x,y)=\begin{cases} -\sum_{x\le z\le y}\mu(x,z)&\text{if }x\lt y,\\ 1&\text{if }x=y,\\ 0&\text{if }x\not\le y. \end{cases} }[/math]
To see the equivalence between this definition and the inversion of zeta function, we may have the following proposition, which is proved by directly evaluating [math]\displaystyle{ \mu\zeta }[/math].
Proposition - For any [math]\displaystyle{ x,y\in P }[/math],
- [math]\displaystyle{ \sum_{x\le z\le y}\mu(x,z)=\begin{cases}1 &\text{if }x=y,\\ 0 &\text{otherwise.}\end{cases} }[/math]
- For any [math]\displaystyle{ x,y\in P }[/math],
Proof. It holds that
- [math]\displaystyle{ (\mu\zeta)(x,y)=\sum_{x\le z\le y}\mu(x,z)\zeta(z,y)=\sum_{x\le z\le y}\mu(x,z) }[/math].
On the other hand, [math]\displaystyle{ \mu\zeta=I }[/math], i.e.
- [math]\displaystyle{ (\mu\zeta)(x,y)=\begin{cases}1 &\text{if }x=y,\\ 0 &\text{otherwise.}\end{cases} }[/math]
The proposition follows.
- [math]\displaystyle{ \square }[/math]
Note that [math]\displaystyle{ \mu(x,y)=\sum_{x\le z\le y}\mu(x,z)-\sum_{x\le z\lt y}\mu(x,z) }[/math], which gives the above inductive definition of Möbius function.
Principle of Möbius inversion
Möbius inversion formula - Let [math]\displaystyle{ P }[/math] be a finite poset and [math]\displaystyle{ \mu }[/math] its Möbius function. Let [math]\displaystyle{ f,g:P\rightarrow \mathbb{R} }[/math]. Then
- [math]\displaystyle{ \forall x\in P,\,\, g(x)=\sum_{y\le x} f(y) }[/math],
- if and only if
- [math]\displaystyle{ \forall x\in P,\,\, f(x)=\sum_{y\le x}g(y)\mu(y,x) }[/math].
- Let [math]\displaystyle{ P }[/math] be a finite poset and [math]\displaystyle{ \mu }[/math] its Möbius function. Let [math]\displaystyle{ f,g:P\rightarrow \mathbb{R} }[/math]. Then
Möbius inversion formula, dual form - Let [math]\displaystyle{ P }[/math] be a finite poset and [math]\displaystyle{ \mu }[/math] its Möbius function. Let [math]\displaystyle{ f,g:P\rightarrow \mathbb{R} }[/math]. Then
- [math]\displaystyle{ \forall x\in P, \,\, g(x)=\sum_{y{\color{red}\ge} x} f(y) }[/math],
- if and only if
- [math]\displaystyle{ \forall x\in P, \,\, f(x)=\sum_{y{\color{red}\ge} x}g(y)\mu(y,x) }[/math].
- Let [math]\displaystyle{ P }[/math] be a finite poset and [math]\displaystyle{ \mu }[/math] its Möbius function. Let [math]\displaystyle{ f,g:P\rightarrow \mathbb{R} }[/math]. Then
Reference
- Stanley, Enumerative Combinatorics, Volume 1, Chapter 2.
- van Lin and Wilson, A course in combinatorics, Chapter 10, 15.