概率论与数理统计 (Spring 2024)/Karger's min-cut algorithm: Difference between revisions
| (15 intermediate revisions by the same user not shown) | |||
| Line 9: | Line 9: | ||
等价地,该问题要求找到一个将 <math>V</math> 分成两个不相交非空子集 <math>S</math> 和 <math>T</math> 的划分,使得跨越 <math>S</math> 和 <math>T</math> 的边总数最小。 | 等价地,该问题要求找到一个将 <math>V</math> 分成两个不相交非空子集 <math>S</math> 和 <math>T</math> 的划分,使得跨越 <math>S</math> 和 <math>T</math> 的边总数最小。 | ||
我们考虑如下更具一般性的情境:输入图 <math>G</math> 可以是'''多重图'''('''multigraph'''),这意味着任意两个顶点 <math>u</math> 和 <math>v</math> 之间可能存在多条'''平行边'''('''parallel edges''' | 我们考虑如下更具一般性的情境:输入图 <math>G</math> 可以是'''多重图'''('''multigraph'''),这意味着任意两个顶点 <math>u</math> 和 <math>v</math> 之间可能存在多条'''平行边'''('''parallel edges'''),也称为'''重'''(读音chóng)'''边'''。多重图中的割的定义与之前相同,割 <math>C</math> 的大小则由 <math>C</math> 中所有边(包括平行边)的总数给出。等价地,可以将多重图视为带有整数边权重的图,割 <math>C</math> 的大小表示为 <math>C</math> 中所有边的总权重。 | ||
通过[http://en.wikipedia.org/wiki/Max-flow_min-cut_theorem 最大流-最小割定理],可以得到这个问题的一个经典的确定性算法。最大流算法可以找到一个最小的'''<math>s</math>-<math>t</math>割''', 将由输入任意指定的一个'''源点''' <math>s\in V</math> 和一个'''汇点''' <math>t\in V</math> 分割开来。然后可以通过穷举来找到针对任意固定源点 <math>s</math> 和所有可能的汇点 <math>t\neq s</math> 的最小 <math>s</math>-<math>t</math> 割,从而求得全局最小割。 | 通过[http://en.wikipedia.org/wiki/Max-flow_min-cut_theorem 最大流-最小割定理],可以得到这个问题的一个经典的确定性算法。最大流算法可以找到一个最小的'''<math>s</math>-<math>t</math>割''', 将由输入任意指定的一个'''源点''' <math>s\in V</math> 和一个'''汇点''' <math>t\in V</math> 分割开来。然后可以通过穷举来找到针对任意固定源点 <math>s</math> 和所有可能的汇点 <math>t\neq s</math> 的最小 <math>s</math>-<math>t</math> 割,从而求得全局最小割。 | ||
| Line 15: | Line 15: | ||
== Karger算法 == | == Karger算法 == | ||
我们将描述一个简洁优美的随机化算法来解决最小割问题。该算法最初是由[http://people.csail.mit.edu/karger/ David Karger]提出的。 | 我们将描述一个简洁优美的随机化算法来解决最小割问题。该算法最初是由[http://people.csail.mit.edu/karger/ David Karger]提出的。 | ||
给定一个多重图 <math>G(V,E)</math> 和一条边 <math>e\in E</math>,我们定义如下的'''收缩'''操作 <math>\mathsf{Contract}(G,e)</math>,将 <math>G</math> 更新为一个新的多重图。 | 给定一个多重图 <math>G(V,E)</math> 和一条边 <math>e\in E</math>,我们定义如下的'''收缩'''操作 <math>\mathsf{Contract}(G,e)</math>,将 <math>G</math> 更新为一个新的多重图。 | ||
| Line 21: | Line 20: | ||
设 <math>e=\{u,v\}</math>: | 设 <math>e=\{u,v\}</math>: | ||
:* 将顶点 <math>u,v</math> 替换为一个新顶点 <math>x</math>; | :* 将顶点 <math>u,v</math> 替换为一个新顶点 <math>x</math>; | ||
:* 对于图中任何一条连接 <math>u,v</math> 其中之一到 <math>u,v</math> 以外某顶点 <math>w\in V\setminus{u,v}</math> | :* 对于图中任何一条连接 <math>u,v</math> 其中之一到 <math>u,v</math> 以外某顶点 <math>w\in V\setminus\{u,v\}</math> 的边,用一条新边 <math>\{x,w\}</math> 替换它; | ||
:* 图中剩余的部分保持不变。 | :* 图中剩余的部分保持不变。 | ||
}} | }} | ||
| Line 36: | Line 35: | ||
---- | ---- | ||
:while <math>|V|>2</math> do | :while <math>|V|>2</math> do | ||
:* | :* 从当前图中均匀分布地选择一条随机的边 <math>e\in E</math>; | ||
:* <math>G=\mathsf{Contract}(G,e)</math>; | :* <math>G=\mathsf{Contract}(G,e)</math>; | ||
:return <math>C=E</math> (即当前所剩的最后两个顶点之间所有的平行边); | :return <math>C=E</math> (即当前所剩的最后两个顶点之间所有的平行边); | ||
| Line 47: | Line 46: | ||
== Karger算法的分析 == | == Karger算法的分析 == | ||
假设输入图 <math>G</math> 为一任意给定的多重图。Karger算法输出了该图的一个随机的割。我们需要分析该随机割是最小割的概率,即如下概率的下界: | 假设输入图 <math>G</math> 为一任意给定的多重图。Karger算法输出了该图的一个随机的割。我们需要分析该随机割是最小割的概率,即如下概率的下界: | ||
:<math>\Pr[\,\text{收缩算法输出了 }G\text{ 的一个最小割}\,]</math> | :<math>\Pr[\,\text{收缩算法输出了 }G\text{ 的一个最小割}\,]</math>. | ||
对此,我们证明如下更强的结论。令 <math>C</math> 是输入图 <math>G</math> 中的某个特定的最小割。我们将分析如下概率的下界: | 对此,我们证明如下更强的结论。令 <math>C</math> 是输入图 <math>G</math> 中的某个特定的最小割。我们将分析如下概率的下界: | ||
:<math>\Pr[\,\text{收缩算法输出了 }C\,]</math> | :<math>\Pr[\,\text{收缩算法输出了 }C\,]</math>. | ||
显然这一概率是收缩算法成功输出最小割的概率的下界(在这里我们使用了如下概率法则:对任意事件 <math>A</math> 和 <math>B</math>,若 <math>A\subseteq B</math>,则<math>\Pr(A)\le \Pr(B)</math>)。 | 显然这一概率是收缩算法成功输出最小割的概率的下界(在这里我们使用了如下概率法则:对任意事件 <math>A</math> 和 <math>B</math>,若 <math>A\subseteq B</math>,则<math>\Pr(A)\le \Pr(B)</math>)。 | ||
| Line 72: | Line 71: | ||
:<math>\Pr[\,\text{收缩算法输出了 }C\,]=\Pr[\,e_1,e_2,\ldots,e_{n-2}\not\in C\,]</math>; | :<math>\Pr[\,\text{收缩算法输出了 }C\,]=\Pr[\,e_1,e_2,\ldots,e_{n-2}\not\in C\,]</math>; | ||
再根据链式法则,这一概率可被计算如下: | 再根据链式法则,这一概率可被计算如下: | ||
:<math>\Pr[\,e_1,e_2,\ldots,e_{n-2}\not\in C\,]=\prod_{i=1}^{n-2}\Pr[\,e_i\not\in C\mid e_1,e_2,\ldots,e_{i-1}\not\in C\,]</math> | :<math>\Pr[\,e_1,e_2,\ldots,e_{n-2}\not\in C\,]=\prod_{i=1}^{n-2}\Pr[\,e_i\not\in C\mid e_1,e_2,\ldots,e_{i-1}\not\in C\,]</math>. | ||
接下来我们的任务是对每个条件概率 <math>\Pr[\,e_i\not\in C\mid e_1,e_2,\ldots,e_{i-1}\not\in C\,]</math> 给出下界。注意到:根据'''引理1''',条件 <math>e_1,e_2,\ldots,e_{i-1}\not\in C</math> 的发生意味着 <math>C</math> 仍是当前图 <math>G_i</math> 中的最小割;而 <math>e_i</math> 是图 <math>G_i</math> 中的一条均匀分布的随机边。于是条件概率 <math>\Pr[\,e_i\not\in C\mid e_1,e_2,\ldots,e_{i-1}\not\in C\,]</math> 即为图 <math>G_i</math> 中一条均匀随机边未命中其某个最小割 <math>C</math> 的概率。直观上:“最小”割应该在边集中相对稀疏,因此这一概率应该有下界。如下引理严格印证了这一直觉。 | 接下来我们的任务是对每个条件概率 <math>\Pr[\,e_i\not\in C\mid e_1,e_2,\ldots,e_{i-1}\not\in C\,]</math> 给出下界。注意到:根据'''引理1''',条件 <math>e_1,e_2,\ldots,e_{i-1}\not\in C</math> 的发生意味着 <math>C</math> 仍是当前图 <math>G_i</math> 中的最小割;而 <math>e_i</math> 是图 <math>G_i</math> 中的一条均匀分布的随机边。于是条件概率 <math>\Pr[\,e_i\not\in C\mid e_1,e_2,\ldots,e_{i-1}\not\in C\,]</math> 即为图 <math>G_i</math> 中一条均匀随机边未命中其某个最小割 <math>C</math> 的概率。直观上:“最小”割应该在边集中相对稀疏,因此这一概率应该有下界。如下引理严格印证了这一直觉。 | ||
| Line 86: | Line 85: | ||
令 <math>V_i</math> 和 <math>E_i</math> 分别表示多重图 <math>G_i</math> 的顶点集和边集。注意到 <math>|V_{i}|=n-i+1</math>。根据'''引理2''',若 <math>C</math> 在 <math>G_i</math> 中仍然是一个最小割,则有 <math>|E_i|\ge \frac{(n-i+2)|C|}{2}</math>。于是条件概率 <math>\Pr[\,e_i\not\in C\mid e_1,e_2,\ldots,e_{i-1}\not\in C\,]</math>可被计算如下: | 令 <math>V_i</math> 和 <math>E_i</math> 分别表示多重图 <math>G_i</math> 的顶点集和边集。注意到 <math>|V_{i}|=n-i+1</math>。根据'''引理2''',若 <math>C</math> 在 <math>G_i</math> 中仍然是一个最小割,则有 <math>|E_i|\ge \frac{(n-i+2)|C|}{2}</math>。于是条件概率 <math>\Pr[\,e_i\not\in C\mid e_1,e_2,\ldots,e_{i-1}\not\in C\,]</math>可被计算如下: | ||
:<math> | :<math> | ||
\begin{align} | \begin{align} | ||
\Pr[\,e_i\not\in C\mid e_1,e_2,\ldots,e_{i-1}\not\in C\,] | \Pr[\,e_i\not\in C\mid e_1,e_2,\ldots,e_{i-1}\not\in C\,] | ||
&=1-\frac{|C|}{|E_i|}\\ | &=1-\frac{|C|}{|E_i|}\\ | ||
&\ge 1-\frac{2}{n-i+1} | &\ge 1-\frac{2}{n-i+1}. | ||
\end{align}</math> | \end{align}</math> | ||
| Line 112: | Line 110: | ||
这证明了如下定理: | 这证明了如下定理: | ||
{{Theorem | {{Theorem | ||
| | |定理(收缩算法的正确概率)| | ||
: | :对于 <math>n</math> 个顶点的任意多重图,收缩算法返回一个最小割的概率至少为 <math>\frac{2}{n(n-1)}</math>。 | ||
}} | }} | ||
初看之下,这一成功概率似乎相当小。然而请注意,一个图中可能存在指数多的割(因为潜在地,每个非空点集 <math>S\subset V</math> 都可以对应一个将 <math>S</math> 与其补集分开的割),而Karger算法有效地将这个指数级的解空间事实上缩小到了平方级别。 | 初看之下,这一成功概率似乎相当小。然而请注意,一个图中可能存在指数多的割(因为潜在地,每个非空点集 <math>S\subset V</math> 都可以对应一个将 <math>S</math> 与其补集分开的割),而Karger算法有效地将这个指数级的解空间事实上缩小到了平方级别。 | ||
| Line 127: | Line 125: | ||
&1-\left(\frac{1}{\mathrm{e}}\right)^{\ln n}\\ | &1-\left(\frac{1}{\mathrm{e}}\right)^{\ln n}\\ | ||
= | = | ||
&1-\frac{1}{n} | &1-\frac{1}{n}. | ||
\end{align}</math> | \end{align}</math> | ||
== | == 一个概率法推论 == | ||
上述对Karger算法的分析可以导出如下关于图中最小割数量的推论。 | |||
{{Theorem| | {{Theorem|推论(最小割数量上界)| | ||
: | :对于 <math>n</math> 个顶点的任意多重图 <math>G(V,E)</math>,<math>G</math> 中最小割的数量至多为 <math>\frac{n(n-1)}{2}</math>。 | ||
}} | }} | ||
{{Proof| | {{Proof| | ||
首先定义事件 <math>A</math> 如下: | |||
:<math>A:</math> “收缩算法输出了图 <math>G</math> 的某个最小割”。 | |||
并对 <math>G</math> 中每一个不同的最小割 <math>C</math>,定义事件 <math>A_C</math> 如下: | |||
:<math>A_C:</math> “收缩算法输出了 <math>C</math>”。 | |||
容易验证,对于图 <math>G</math> 中的不同最小割 <math>C</math>,事件 <math>A_C</math> 彼此不相容;而且,事件 <math>A</math> 是对所有最小割 <math>C</math> 事件 <math>A_C</math> 的并,即 | |||
:<math>A=\bigcup_{G\text{中所有最小割}C}A_C</math>. | |||
于是根据概率的 <math>\sigma</math>可加性,有: | |||
:<math>\Pr(A)=\sum_{G\text{中所有最小割}C}\Pr(A_C)</math>. | |||
:<math> | |||
</math> | |||
由我们对于Karger算法的分析可得,对任何最小割 <math>C</math>,都有 <math>\Pr(A_c)\ge\frac{2}{n(n-1)}</math>。而作为良定义的概率,必然有 <math>\Pr(A)\le 1</math>。因此可知,图 <math>G</math> 中最小割的总数不会超过 <math>\frac{n(n-1)}{2}</math>。 | |||
}} | }} | ||
上述推论是一个'''概率法'''('''the probabilistic method''')的实例:结论本身不具有任何随机性,但是其证明过程引入了概率论。而且这个结论给出的界是紧的:存在 <math>n</math> 个顶点的图 <math>G</math>,其最小割的个数刚好为 <math>\frac{n(n-1)}{2}</math>,例如:<math>n</math> 个顶点的环。 | |||
Latest revision as of 14:44, 19 March 2024
令 [math]\displaystyle{ G(V, E) }[/math] 是一个无向图。我们称边集 [math]\displaystyle{ C\subseteq E }[/math] 是图 [math]\displaystyle{ G }[/math] 的一个割,如果图 [math]\displaystyle{ G }[/math] 在删除所有 [math]\displaystyle{ C }[/math] 中的边后变得不连通。
最小割问题, 也称为全局最小割问题, 定义如下。
全局最小割问题 - 输入:无向图 [math]\displaystyle{ G(V,E) }[/math];
- 输出:图 [math]\displaystyle{ G }[/math] 中具有最小 [math]\displaystyle{ |C| }[/math] 的割 [math]\displaystyle{ C }[/math]。
等价地,该问题要求找到一个将 [math]\displaystyle{ V }[/math] 分成两个不相交非空子集 [math]\displaystyle{ S }[/math] 和 [math]\displaystyle{ T }[/math] 的划分,使得跨越 [math]\displaystyle{ S }[/math] 和 [math]\displaystyle{ T }[/math] 的边总数最小。
我们考虑如下更具一般性的情境:输入图 [math]\displaystyle{ G }[/math] 可以是多重图(multigraph),这意味着任意两个顶点 [math]\displaystyle{ u }[/math] 和 [math]\displaystyle{ v }[/math] 之间可能存在多条平行边(parallel edges),也称为重(读音chóng)边。多重图中的割的定义与之前相同,割 [math]\displaystyle{ C }[/math] 的大小则由 [math]\displaystyle{ C }[/math] 中所有边(包括平行边)的总数给出。等价地,可以将多重图视为带有整数边权重的图,割 [math]\displaystyle{ C }[/math] 的大小表示为 [math]\displaystyle{ C }[/math] 中所有边的总权重。
通过最大流-最小割定理,可以得到这个问题的一个经典的确定性算法。最大流算法可以找到一个最小的[math]\displaystyle{ s }[/math]-[math]\displaystyle{ t }[/math]割, 将由输入任意指定的一个源点 [math]\displaystyle{ s\in V }[/math] 和一个汇点 [math]\displaystyle{ t\in V }[/math] 分割开来。然后可以通过穷举来找到针对任意固定源点 [math]\displaystyle{ s }[/math] 和所有可能的汇点 [math]\displaystyle{ t\neq s }[/math] 的最小 [math]\displaystyle{ s }[/math]-[math]\displaystyle{ t }[/math] 割,从而求得全局最小割。
Karger算法
我们将描述一个简洁优美的随机化算法来解决最小割问题。该算法最初是由David Karger提出的。
给定一个多重图 [math]\displaystyle{ G(V,E) }[/math] 和一条边 [math]\displaystyle{ e\in E }[/math],我们定义如下的收缩操作 [math]\displaystyle{ \mathsf{Contract}(G,e) }[/math],将 [math]\displaystyle{ G }[/math] 更新为一个新的多重图。
收缩算子 [math]\displaystyle{ \mathsf{Contract}(G,e) }[/math] 设 [math]\displaystyle{ e=\{u,v\} }[/math]:
- 将顶点 [math]\displaystyle{ u,v }[/math] 替换为一个新顶点 [math]\displaystyle{ x }[/math];
- 对于图中任何一条连接 [math]\displaystyle{ u,v }[/math] 其中之一到 [math]\displaystyle{ u,v }[/math] 以外某顶点 [math]\displaystyle{ w\in V\setminus\{u,v\} }[/math] 的边,用一条新边 [math]\displaystyle{ \{x,w\} }[/math] 替换它;
- 图中剩余的部分保持不变。
换言之,[math]\displaystyle{ \mathsf{Contract}(G,\{u,v\}) }[/math] 将两个顶点 [math]\displaystyle{ u }[/math] 和 [math]\displaystyle{ v }[/math] 合并成一个新顶点 [math]\displaystyle{ x }[/math],该新顶点邻接的边保留了原始图 [math]\displaystyle{ G }[/math] 中与 [math]\displaystyle{ u,v }[/math] 两顶点之一邻接的边(但不包括二者之间的平行边 [math]\displaystyle{ \{u,v\} }[/math])。现在我们应该能意识到为什么我们考虑多重图而不是简单图——因为即使我们从没有平行边的简单图开始,收缩操作也可能引入平行边。
收缩操作的效果如图所示:
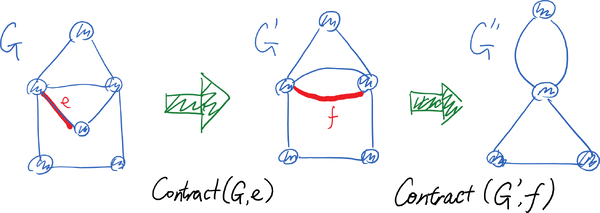
Karger算法的想法很简单:在每一步中,随机选择当前多重图中的一条边,将其收缩;重复这一操作,直至图中只剩下两个顶点——这两个剩下的顶点之间的所有边的集合,必然是最初图(乃至每一步中的图)中的一个割。
收缩算法 (Karger 1993) - 输入: 多重图 [math]\displaystyle{ G(V,E) }[/math];
- while [math]\displaystyle{ |V|\gt 2 }[/math] do
- 从当前图中均匀分布地选择一条随机的边 [math]\displaystyle{ e\in E }[/math];
- [math]\displaystyle{ G=\mathsf{Contract}(G,e) }[/math];
- return [math]\displaystyle{ C=E }[/math] (即当前所剩的最后两个顶点之间所有的平行边);
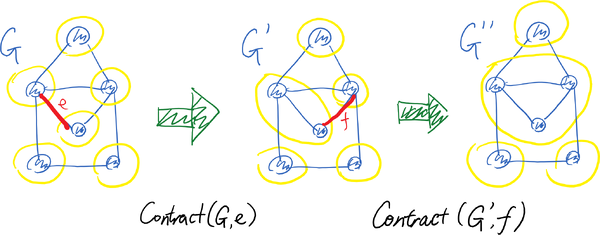
另一种看待收缩操作 [math]\displaystyle{ \mathsf{Contract}(G,e) }[/math] 的方式是将其解读为对两个顶点的等价类的合并。假设 [math]\displaystyle{ V={v_1,v_2,\ldots,v_n} }[/math] 是所有顶点的集合。我们从 [math]\displaystyle{ n }[/math] 个顶点等价类 [math]\displaystyle{ S_1,S_2,\ldots, S_n }[/math] 开始,其中每个等价类 [math]\displaystyle{ S_i={v_i} }[/math] 包含一个顶点。通过调用 [math]\displaystyle{ \mathsf{Contract}(G,e) }[/math],其中 [math]\displaystyle{ e }[/math] 跨越了两个不同的等价类 [math]\displaystyle{ S_i }[/math] 和 [math]\displaystyle{ S_j }[/math],其效果是将等价类 [math]\displaystyle{ S_i }[/math] 和 [math]\displaystyle{ S_j }[/math] 合并。收缩后的多重图中的边就是跨越不同顶点等价类之间的边。 这一视角的效果如图所示:
Karger算法的分析
假设输入图 [math]\displaystyle{ G }[/math] 为一任意给定的多重图。Karger算法输出了该图的一个随机的割。我们需要分析该随机割是最小割的概率,即如下概率的下界:
- [math]\displaystyle{ \Pr[\,\text{收缩算法输出了 }G\text{ 的一个最小割}\,] }[/math].
对此,我们证明如下更强的结论。令 [math]\displaystyle{ C }[/math] 是输入图 [math]\displaystyle{ G }[/math] 中的某个特定的最小割。我们将分析如下概率的下界:
- [math]\displaystyle{ \Pr[\,\text{收缩算法输出了 }C\,] }[/math].
显然这一概率是收缩算法成功输出最小割的概率的下界(在这里我们使用了如下概率法则:对任意事件 [math]\displaystyle{ A }[/math] 和 [math]\displaystyle{ B }[/math],若 [math]\displaystyle{ A\subseteq B }[/math],则[math]\displaystyle{ \Pr(A)\le \Pr(B) }[/math])。
我们引入以下记号:
- 令 [math]\displaystyle{ e_1,e_2,\ldots,e_{n-2} }[/math] 表示在运行收缩算法时,依次选中进行收缩的随机边的序列;
- 令 [math]\displaystyle{ G_1=G }[/math] 表示最初输入的多重图。对于 [math]\displaystyle{ i=1,2,\ldots,n-2 }[/math],令 [math]\displaystyle{ G_{i+1}=\mathsf{Contract}(G_{i},e_i) }[/math] 表示第 [math]\displaystyle{ i }[/math] 轮收缩后的多重图。
我们可以做出如下的观察:
引理 1 - 如果 [math]\displaystyle{ C }[/math] 是多重图 [math]\displaystyle{ G }[/math] 中的一个最小割,且 [math]\displaystyle{ e\not\in C }[/math],那么 [math]\displaystyle{ C }[/math] 在收缩图 [math]\displaystyle{ G'=\mathsf{Contract}(G,e) }[/math] 中仍然是一个最小割。
Proof. 我们首先观察到,收缩永远不会创建新的割:收缩图 [math]\displaystyle{ G' }[/math] 中的每个割也必定是原图 [math]\displaystyle{ G }[/math] 中的一个割。
然后我们观察到,原始图 [math]\displaystyle{ G }[/math] 中的割 [math]\displaystyle{ C }[/math] 能在收缩图 [math]\displaystyle{ G' }[/math] 中幸存,当且仅当收缩边 [math]\displaystyle{ e\not\in C }[/math]。
这两个观察都很容易通过收缩操作的定义进行验证(特别是在考虑顶点等价类的解释时更容易验证)。
- [math]\displaystyle{ \square }[/math]
根据引理1,我们有:
- [math]\displaystyle{ \Pr[\,\text{收缩算法输出了 }C\,]=\Pr[\,e_1,e_2,\ldots,e_{n-2}\not\in C\,] }[/math];
再根据链式法则,这一概率可被计算如下:
- [math]\displaystyle{ \Pr[\,e_1,e_2,\ldots,e_{n-2}\not\in C\,]=\prod_{i=1}^{n-2}\Pr[\,e_i\not\in C\mid e_1,e_2,\ldots,e_{i-1}\not\in C\,] }[/math].
接下来我们的任务是对每个条件概率 [math]\displaystyle{ \Pr[\,e_i\not\in C\mid e_1,e_2,\ldots,e_{i-1}\not\in C\,] }[/math] 给出下界。注意到:根据引理1,条件 [math]\displaystyle{ e_1,e_2,\ldots,e_{i-1}\not\in C }[/math] 的发生意味着 [math]\displaystyle{ C }[/math] 仍是当前图 [math]\displaystyle{ G_i }[/math] 中的最小割;而 [math]\displaystyle{ e_i }[/math] 是图 [math]\displaystyle{ G_i }[/math] 中的一条均匀分布的随机边。于是条件概率 [math]\displaystyle{ \Pr[\,e_i\not\in C\mid e_1,e_2,\ldots,e_{i-1}\not\in C\,] }[/math] 即为图 [math]\displaystyle{ G_i }[/math] 中一条均匀随机边未命中其某个最小割 [math]\displaystyle{ C }[/math] 的概率。直观上:“最小”割应该在边集中相对稀疏,因此这一概率应该有下界。如下引理严格印证了这一直觉。
引理 2 - 如果 [math]\displaystyle{ C }[/math] 是多重图 [math]\displaystyle{ G(V,E) }[/math] 中的一个最小割,那么 [math]\displaystyle{ |E|\ge \frac{|V||C|}{2} }[/math]。
Proof. - 注意到每个顶点 [math]\displaystyle{ v\in V }[/math] 的度数必然至少为 [math]\displaystyle{ |C| }[/math],否则所有与 [math]\displaystyle{ v }[/math] 邻接的边即构成了一个割(将点 [math]\displaystyle{ v }[/math] 与其余所有点分开),而且这个割比 [math]\displaystyle{ |C| }[/math] 更小,这就与 [math]\displaystyle{ C }[/math] 是一个最小割相矛盾。
- 现在由于每个顶点的度至少为 [math]\displaystyle{ |C| }[/math],应用握手引理,所有顶点度数之和是 [math]\displaystyle{ 2|E|\ge |V||C| }[/math]。(容易验证握手引理对于多重图仍旧成立。)
- [math]\displaystyle{ \square }[/math]
令 [math]\displaystyle{ V_i }[/math] 和 [math]\displaystyle{ E_i }[/math] 分别表示多重图 [math]\displaystyle{ G_i }[/math] 的顶点集和边集。注意到 [math]\displaystyle{ |V_{i}|=n-i+1 }[/math]。根据引理2,若 [math]\displaystyle{ C }[/math] 在 [math]\displaystyle{ G_i }[/math] 中仍然是一个最小割,则有 [math]\displaystyle{ |E_i|\ge \frac{(n-i+2)|C|}{2} }[/math]。于是条件概率 [math]\displaystyle{ \Pr[\,e_i\not\in C\mid e_1,e_2,\ldots,e_{i-1}\not\in C\,] }[/math]可被计算如下:
- [math]\displaystyle{ \begin{align} \Pr[\,e_i\not\in C\mid e_1,e_2,\ldots,e_{i-1}\not\in C\,] &=1-\frac{|C|}{|E_i|}\\ &\ge 1-\frac{2}{n-i+1}. \end{align} }[/math]
将上述分析归总,可得:
- [math]\displaystyle{ \begin{align} \Pr[\,\text{收缩算法输出了 }G\text{ 的一个最小割}\,] &\ge \Pr[\,\text{收缩算法输出了 }C\,]\\ &= \Pr[\,e_1,e_2,\ldots,e_{n-2}\not\in C\,]\\ &= \prod_{i=1}^{n-2}\Pr[\,e_i\not\in C\mid e_1,e_2,\ldots,e_{i-1}\not\in C\,]\\ &\ge \prod_{i=1}^{n-2}\left(1-\frac{2}{n-i+1}\right)\\ &= \prod_{k=3}^{n}\frac{k-2}{k}\\ &= \frac{2}{n(n-1)}. \end{align} }[/math]
这证明了如下定理:
定理(收缩算法的正确概率) - 对于 [math]\displaystyle{ n }[/math] 个顶点的任意多重图,收缩算法返回一个最小割的概率至少为 [math]\displaystyle{ \frac{2}{n(n-1)} }[/math]。
初看之下,这一成功概率似乎相当小。然而请注意,一个图中可能存在指数多的割(因为潜在地,每个非空点集 [math]\displaystyle{ S\subset V }[/math] 都可以对应一个将 [math]\displaystyle{ S }[/math] 与其补集分开的割),而Karger算法有效地将这个指数级的解空间事实上缩小到了平方级别。
我们可以独立地运行上述收缩算法 [math]\displaystyle{ t=\left\lceil\frac{n(n-1)\ln n}{2}\right\rceil }[/math] 次,将所有返回的割中最小的一个作为最终结果返回。最终正确得到最小割的概率至少是:
- [math]\displaystyle{ \begin{align} &1-\Pr[\,\text{全部 }t\text{ 次独立运行收缩算法都没有找到 }G\text{ 的最小割}\,] \\ = &1-\Pr[\,\text{一次运行收缩算法没有成功输出 }G\text{ 的最小割}\,]^{t} \\ \ge &1- \left(1-\frac{2}{n(n-1)}\right)^{\frac{n(n-1)}{2}\cdot \ln n} \\ \ge &1-\left(\frac{1}{\mathrm{e}}\right)^{\ln n}\\ = &1-\frac{1}{n}. \end{align} }[/math]
一个概率法推论
上述对Karger算法的分析可以导出如下关于图中最小割数量的推论。
推论(最小割数量上界) - 对于 [math]\displaystyle{ n }[/math] 个顶点的任意多重图 [math]\displaystyle{ G(V,E) }[/math],[math]\displaystyle{ G }[/math] 中最小割的数量至多为 [math]\displaystyle{ \frac{n(n-1)}{2} }[/math]。
Proof. 首先定义事件 [math]\displaystyle{ A }[/math] 如下:
- [math]\displaystyle{ A: }[/math] “收缩算法输出了图 [math]\displaystyle{ G }[/math] 的某个最小割”。
并对 [math]\displaystyle{ G }[/math] 中每一个不同的最小割 [math]\displaystyle{ C }[/math],定义事件 [math]\displaystyle{ A_C }[/math] 如下:
- [math]\displaystyle{ A_C: }[/math] “收缩算法输出了 [math]\displaystyle{ C }[/math]”。
容易验证,对于图 [math]\displaystyle{ G }[/math] 中的不同最小割 [math]\displaystyle{ C }[/math],事件 [math]\displaystyle{ A_C }[/math] 彼此不相容;而且,事件 [math]\displaystyle{ A }[/math] 是对所有最小割 [math]\displaystyle{ C }[/math] 事件 [math]\displaystyle{ A_C }[/math] 的并,即
- [math]\displaystyle{ A=\bigcup_{G\text{中所有最小割}C}A_C }[/math].
于是根据概率的 [math]\displaystyle{ \sigma }[/math]可加性,有:
- [math]\displaystyle{ \Pr(A)=\sum_{G\text{中所有最小割}C}\Pr(A_C) }[/math].
由我们对于Karger算法的分析可得,对任何最小割 [math]\displaystyle{ C }[/math],都有 [math]\displaystyle{ \Pr(A_c)\ge\frac{2}{n(n-1)} }[/math]。而作为良定义的概率,必然有 [math]\displaystyle{ \Pr(A)\le 1 }[/math]。因此可知,图 [math]\displaystyle{ G }[/math] 中最小割的总数不会超过 [math]\displaystyle{ \frac{n(n-1)}{2} }[/math]。
- [math]\displaystyle{ \square }[/math]
上述推论是一个概率法(the probabilistic method)的实例:结论本身不具有任何随机性,但是其证明过程引入了概率论。而且这个结论给出的界是紧的:存在 [math]\displaystyle{ n }[/math] 个顶点的图 [math]\displaystyle{ G }[/math],其最小割的个数刚好为 [math]\displaystyle{ \frac{n(n-1)}{2} }[/math],例如:[math]\displaystyle{ n }[/math] 个顶点的环。