Theory@Suzhou 2025

General Information

苏教楼D在图中红星处

• Sunday, Nov 30, 2025: 9 am--6 pm.
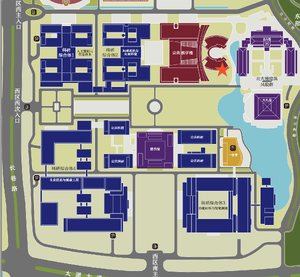
• Location: 南京大学苏州校区
• Venue: 苏教楼D202

苏州校区地图

Speakers (in alphabetic order)

• 陈雪（中国科学技术大学）
• 黄增峰（复旦大学）
• 姜少峰（北京大学）
• 许超（电子科技大学）
• 张驰豪（上海交通大学）
• 张瀚文（哥本哈根大学）
• 张天翼（南京大学）

Guests

不需注册，欢迎所有对理论计算机科学感兴趣的同学和老师前来参加。 请 简单填写问卷 用于统计参会人数，以便准备茶歇的食物和调整报告厅。

Workshop Program
09:00 - 09:50	张天翼 南京大学	Title: Approximate Light Spanners in Planar Graphs Abstract: Althöfer 等人（DCG 1993）提出了贪心生成子图，并证明了对于任意带权平面图 [math]\displaystyle{ G }[/math]，其贪心 [math]\displaystyle{ (1+\epsilon) }[/math]-生成子图的总权重至多为 [math]\displaystyle{ \left(1 + \frac{2}{\epsilon}\right) \cdot w(\mathrm{MST}(G)) }[/math]，其中 [math]\displaystyle{ w(\mathrm{MST}(G)) }[/math] 表示图 [math]\displaystyle{ G }[/math] 的最小生成树 [math]\displaystyle{ \mathrm{MST}(G) }[/math] 的权重。该界在存在性意义上是紧的：存在某些平面图 [math]\displaystyle{ G }[/math]，使得其任意 [math]\displaystyle{ (1+\epsilon) }[/math]-生成子图的权重至少为 [math]\displaystyle{ \left(1 + \frac{2}{\epsilon}\right) \cdot w(\mathrm{MST}(G)) }[/math]。 然而，从近似算法的角度来看，即使是双标准（bicriteria）近似，贪心生成子图 的权重近似因子也基本上达到了上述存在性下界：存在某些平面图 [math]\displaystyle{ G }[/math]，使得对于任意满足 [math]\displaystyle{ 1 \leq x = O(\epsilon^{-1/2}) }[/math] 的参数，其贪心 [math]\displaystyle{ (1 + x\epsilon) }[/math]-生成子图 的权重为 [math]\displaystyle{ \Omega\left(\frac{1}{\epsilon \cdot x^2} \cdot w(G_{\mathrm{opt},\epsilon})\right) }[/math]，其中 [math]\displaystyle{ G_{\mathrm{opt},\epsilon} }[/math] 是图 [math]\displaystyle{ G }[/math] 的权重最小的 [math]\displaystyle{ (1+\epsilon) }[/math]-生成子图。 尽管在过去三十年中，关于生成子图的近似算法的研究层出不穷，但目前仍不存在任何（即使是双标准）近似算法，能够在带权平面图上构造出优于上述存在性下界的轻量生成子图。 作为本文的主要贡献，我们提出了一种在平面图上的动态规划算法，可在任意带权平面图 [math]\displaystyle{ G }[/math] 中构造一个 [math]\displaystyle{ \left(1 + \epsilon \cdot 2^{O(\log^* 1/\epsilon)}\right) }[/math]-生成子图，其总权重为 [math]\displaystyle{ O(1) \cdot w(G_{\mathrm{opt},\epsilon}) }[/math]。此外，我们也证明了精确求解最小平面生成子图是NP难的。
Coffee Break (09:50 – 10:15)
10:15 – 11:05	姜少峰 北京大学	Title: Local Search for Clustering in Almost-linear Time Abstract: We propose the first local search algorithm for Euclidean clustering that attains an $O(1)$-approximation in almost-linear time. Specifically, for Euclidean k-Means, our algorithm achieves an $O(c)$-approximation in $\tilde{O}(n^{1 + 1 / c})$ time, for any constant $c \ge 1$, maintaining the same running time as the previous (non-local-search-based) approach [la~Tour and Saulpic, arXiv'2407.11217] while improving the approximation factor from $O(c^{6})$ to $O(c)$. The algorithm generalizes to any metric space with sparse spanners, delivering efficient constant approximation in $\ell_p$ metrics, doubling metrics, Jaccard metrics, etc. This generality derives from our main technical contribution: a local search algorithm on general graphs that obtains an $O(1)$-approximation in almost-linear time. We establish this through a new $1$-swap local search framework featuring a novel swap selection rule. At a high level, this rule ``scores every possible swap, based on both its modification to the clustering and its improvement to the clustering objective, and then selects those high-scoring swaps. To implement this, we design a new data structure for maintaining approximate nearest neighbors with amortized guarantees tailored to our framework.
11:10 – 12:00	陈雪 中国科学技术大学	Title: Algorithms for Sparse LPN and LSPN Against Low-noise Abstract: We consider sparse variants of the classical Learning Parities with random Noise (LPN) problem. Our main contribution is a new algorithmic framework that provides learning algorithms against low-noise for both Learning Sparse Parities (LSPN) problem and sparse LPN problem. Different from previous approaches for LSPN and sparse LPN, this framework has a simple structure and runs in polynomial space. Let [math]\displaystyle{ n }[/math] be the dimension, [math]\displaystyle{ k }[/math] denote the sparsity, and [math]\displaystyle{ \eta }[/math] be the noise rate. As a fundamental problem in computational learning theory, Learning Sparse Parities with Noise (LSPN) assumes the hidden parity is [math]\displaystyle{ k }[/math]-sparse. While a simple enumeration algorithm takes [math]\displaystyle{ {n \choose k}=O((n/k)^k) }[/math] time, previously known results still need [math]\displaystyle{ {n \choose k/2} = \Omega((n/k)^{k/2}) }[/math] time for any noise rate [math]\displaystyle{ \eta }[/math]. Our framework provides a LSPN algorithm runs in time [math]\displaystyle{ O((\eta \cdot n/k)^k) }[/math] for any noise rate [math]\displaystyle{ \eta }[/math], which improves the state-of-the-art of LSPN whenever [math]\displaystyle{ \eta \in ( k/n,\sqrt{k/n}) }[/math]. The sparse LPN problem is closely related to the classical problem of refuting random [math]\displaystyle{ k }[/math]-CSP and has been widely used in cryptography as the hardness assumption. Different from the standard LPN, it samples random [math]\displaystyle{ k }[/math]-sparse vectors. Because the number of [math]\displaystyle{ k }[/math]-sparse vectors is [math]\displaystyle{ {n \choose k} \lt n^k }[/math], sparse LPN has learning algorithms in polynomial time when [math]\displaystyle{ m\gt n^{k/2} }[/math]. However, much less is known about learning algorithms for constant [math]\displaystyle{ k }[/math] like [math]\displaystyle{ 3 }[/math] and [math]\displaystyle{ m\lt n^{k/2} }[/math] samples, except the Gaussian elimination algorithm of time [math]\displaystyle{ e^{\eta n} }[/math]. Our framework provides a learning algorithm in [math]\displaystyle{ e^{O(\eta \cdot n^{\frac{\delta+1}{2}})} }[/math] time given [math]\displaystyle{ \delta \in (0,1) }[/math] and [math]\displaystyle{ m \approx n^{1+(1-\delta)\cdot \frac{k-1}{2}} }[/math] samples. This improves previous learning algorithms. For example, in the classical setting of [math]\displaystyle{ k=3 }[/math] and [math]\displaystyle{ m=n^{1.4} }[/math], our algorithm would be faster than previous approaches for any [math]\displaystyle{ \eta\lt n^{-0.7} }[/math]. Based on joint work with Wenxuan Shu (USTC) and Zhaienhe Zhou (USTC).
Lunch Break (12:00 - 14:00)
14:00 – 14:50	张瀚文 哥本哈根大学	Title: Minimum Star Partitions of Simple Polygons in Polynomial Time Abstract: 我们设计了一种多项式时间算法，用于将简单多边形P划分为最少个数的星形多边形。这样的算法是否存在的问题已被提出超过四十年之久并多次重复，包括在O’Rourke的著作《美术馆定理与算法》中。之前已知的算法只能处理一些特殊情况，例如多边形是单调的直边多边形，或者不允许使用斯坦纳点的情况，都远不足以处理最普遍的例子。而允许星型子部分重叠的覆盖变体——即著名的美术馆问题，在2018年被证明属于∃ℝ完全类，因此很可能比NP问题更难。除了理论价值外，星型多边形划分也可以应用在数控型腔铣削、机器人路径规划、形状参数化等实际场景中。 在这个报告中，我会着重讲解我们求解这个问题时的直觉、思考和发现，沉浸式体验我们在这项研究中的全部经历。
14:50 – 15:40	许超 电子科技大学	Title: An Optimal Algorithm for the Stacker Crane Problem on Fixed Topologies Abstract: The Stacker Crane Problem (SCP) is a variant of the Traveling Salesman Problem. In SCP, pairs of pickup and delivery points are designated on a graph, and a crane must visit these points to move objects from each pickup location to its respective delivery point. The goal is to minimize the total distance traveled. SCP is known to be NP-hard, even on trees. The only positive results, in terms of polynomial-time solvability, apply to graphs that are topologically equivalent to a path or a cycle. We propose an algorithm that is optimal for each fixed topology, running in near-linear time. This is achieved by demonstrating that the problem is fixed-parameter tractable (FPT) when parameterized by both the cycle rank and the number of branch vertices.
Coffee Break (15:40 – 16:15)
16:15 – 17:05	张驰豪 上海交通大学	Title: TBA Abstract:TBA
17:10 – 18:00	黄增峰 复旦大学	Title: TBA Abstract:TBA

Getting to The Campus

• 入校：校外来宾请在校门口向安保说明会议名称后登记入校。
• 高铁 / 动车
  • 苏州站：打车至校区约 30 分钟（非早晚高峰情况下），费用约 ¥30。亦可选择快线 3 号或地铁转有轨电车，全程约 2 小时。
  • 苏州新区站：打车至校区约 25 分钟，费用约 ¥25。也可乘坐有轨电车 2 号线，约 1 小时。
• 飞机
  • 无锡硕放机场（WUX）：打车至校区约 30 分钟；因跨城行驶，司机可能会收取返程/空驶费用，总费用约 ¥80。如果能打到顺风车的话会较为便宜。亦可选公共交通，约 2 小时。
  • 上海虹桥机场（SHA）：建议从虹桥火车站换乘高铁至苏州站或苏州新区站。务必留意，由上海虹桥站前往苏州的高铁末班车时间通常是21:42。不建议从虹桥直接打车至苏州（费用较高）；同时不建议打顺风车，因为通常只能打到黑出租。

Accommodation Suggestion

￥￥￥ 苏州科技城源宿酒店
￥￥ 南大国际学术交流中心（校内酒店，性价比高）、苏州科技城万达美华酒店、全季苏州科技城酒店、苏州高新区科技城亚朵酒店
￥ 格林豪泰苏州市科技城商务酒店、宜必思尚品苏州科技城酒店、如家精选-苏州乐园高新区科技城店

Lunch & Supper

苏州校区的四个食堂在图中红星处

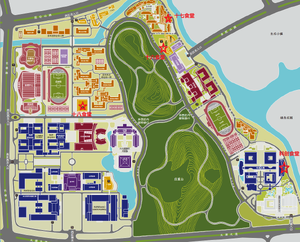
• 苏州校区内现有科创大厦食堂、第16、17、18食堂共四个食堂，素菜2-3元、荤菜4-8元，可直接用支付宝或微信支付。此外，国际学术交流中心也提供更为昂贵的食物。
• 学校附近有：东渚镇、文体中心、丰茂里、时尚水岸星悦荟、星悦里等几个商业区。
• 也可以选择外卖，会送至校门口的外卖柜或外卖架上。

Getting Around

• 大阳山国家森林公园 & 植物园：层林步道＋寺庙人文，爬 60–90 分钟视体力安排；秋冬晴天观景佳。
• 树山生态村：乡野步道、茶园与农家菜，团队晚餐/走读首选。
• 太湖湿地/西山方向：自驾更便捷，观湿地与湖景线。
• 古城园林：傍晚可打车去平江路/山塘街逛夜景，或白天参观苏州博物馆/拙政园。

About Suzhou Campus

南京大学苏州校区位于苏州高新区太湖科技城，地处“环太湖科创圈”与“沿沪宁产业创新带”的黄金交汇点，被定位为南大发展壮大新工科的主阵地。立足“国家战略、世界一流、强强联合、需需结合”，南大苏州校区聚焦人工智能、新一代信息技术、新能源、先进制造、生命健康等领域“卡脖子”问题，强化“新工科”建设，促进文理工医交叉融合，政产学研协调发展。

Contact

刘明谋： lmm@nju.edu.cn