高级算法 (Fall 2019)/Concentration of measure

Chernoff Bound

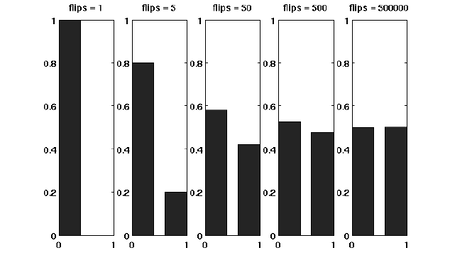
Suppose that we have a fair coin. If we toss it once, then the outcome is completely unpredictable. But if we toss it, say for 1000 times, then the number of HEADs is very likely to be around 500. This phenomenon, as illustrated in the following figure, is called the concentration of measure. The Chernoff bound is an inequality that characterizes the concentration phenomenon for the sum of independent trials.

Before formally stating the Chernoff bound, let's introduce the moment generating function.

Moment generating functions

The more we know about the moments of a random variable $X$, the more information we would have about $X$. There is a so-called moment generating function, which "packs" all the information about the moments of $X$ into one function.

Definition

The moment generating function of a random variable $X$ is defined as $\mathbf{E}\left[{\mathrm{e}}^{\lambda X}\right]$ where $\lambda$ is the parameter of the function.

By Taylor's expansion and the linearity of expectations,

$\begin{array}{rl}\mathbf{E}\left[{\mathrm{e}}^{\lambda X}\right]& =\mathbf{E}\left[\sum _{k=0}^{\mathrm{\infty }}\frac{{\lambda }^k}{k!}{X}^k\right]\\ & =\sum _{k=0}^{\mathrm{\infty }}\frac{{\lambda }^k}{k!}\mathbf{E}\left[X^k\right]\end{array}$

The moment generating function $\mathbf{E}\left[{\mathrm{e}}^{\lambda X}\right]$ is a function of $\lambda$.

The Chernoff bound

The Chernoff bounds are exponentially sharp tail inequalities for the sum of independent trials. The bounds are obtained by applying Markov's inequality to the moment generating function of the sum of independent trials, with some appropriate choice of the parameter $\lambda$.

Chernoff bound (the upper tail)

Let $X=\sum _{i=1}^n{X}_i$, where $X_1,X_2,\dots ,X_n$ are independent Poisson trials. Let $\mu =\mathbf{E}[X]$. Then for any $\delta >0$, $Pr[X\ge (1+\delta )\mu ]\le {\left(\frac{e^{\delta }}{(1+\delta {)}^{(1+\delta )}}\right)}^{\mu }.$

Proof. For any $\lambda >0$, $X\ge (1+\delta )\mu$ is equivalent to that $e^{\lambda X}\ge e^{\lambda (1+\delta )\mu }$, thus $\begin{array}{rl}Pr[X\ge (1+\delta )\mu ]& =Pr[e^{\lambda X}\ge e^{\lambda (1+\delta )\mu }]\\ & \le \frac{\mathbf{E}\left[e^{\lambda X}\right]}{e^{\lambda (1+\delta )\mu }},\end{array}$ where the last step follows by Markov's inequality. Computing the moment generating function $\mathbf{E}[e^{\lambda X}]$: $\begin{array}{rl}\mathbf{E}\left[e^{\lambda X}\right]& =\mathbf{E}\left[e^{\lambda \sum _{i=1}^n{X}_i}\right]\\ & =\mathbf{E}\left[\prod _{i=1}^n{e}^{\lambda X_i}\right]\\ & =\prod _{i=1}^n\mathbf{E}\left[e^{\lambda X_i}\right].& (\text{for independent random variables})\end{array}$ Let $p_i=Pr[X_i=1]$ for $i=1,2,\dots ,n$. Then, $\mu =\mathbf{E}[X]=\mathbf{E}\left[\sum _{i=1}^n{X}_i\right]=\sum _{i=1}^n\mathbf{E}[X_i]=\sum _{i=1}^n{p}_i$. We bound the moment generating function for each individual $X_i$ as follows. $\begin{array}{rl}\mathbf{E}\left[e^{\lambda X_i}\right]& =p_i\cdot e^{\lambda \cdot 1}+(1-p_i)\cdot e^{\lambda \cdot 0}\\ & =1+p_i(e^{\lambda }-1)\\ & \le e^{p_i(e^{\lambda }-1)},\end{array}$ where in the last step we apply the Taylor's expansion so that $e^y\ge 1+y$ where $y=p_i(e^{\lambda }-1)\ge 0$. (By doing this, we can transform the product to the sum of $p_i$, which is $\mu$.) Therefore, $\begin{array}{rl}\mathbf{E}\left[e^{\lambda X}\right]& =\prod _{i=1}^n\mathbf{E}\left[e^{\lambda X_i}\right]\\ & \le \prod _{i=1}^n{e}^{p_i(e^{\lambda }-1)}\\ & =\exp (\sum _{i=1}^n{p}_i(e^{\lambda }-1))\\ & =e^{(e^{\lambda }-1)\mu }.\end{array}$ Thus, we have shown that for any $\lambda >0$, $\begin{array}{rl}Pr[X\ge (1+\delta )\mu ]& \le \frac{\mathbf{E}\left[e^{\lambda X}\right]}{e^{\lambda (1+\delta )\mu }}\\ & \le \frac{e^{(e^{\lambda }-1)\mu }}{e^{\lambda (1+\delta )\mu }}\\ & ={\left(\frac{e^{(e^{\lambda }-1)}}{e^{\lambda (1+\delta )}}\right)}^{\mu }\end{array}$. For any $\delta >0$, we can let $\lambda =\ln (1+\delta )>0$ to get $Pr[X\ge (1+\delta )\mu ]\le {\left(\frac{e^{\delta }}{(1+\delta {)}^{(1+\delta )}}\right)}^{\mu }.$ $◻$

The idea of the proof is actually quite clear: we apply Markov's inequality to $e^{\lambda X}$ and for the rest, we just estimate the moment generating function $\mathbf{E}[e^{\lambda X}]$. To make the bound as tight as possible, we minimized the $\frac{e^{(e^{\lambda }-1)}}{e^{\lambda (1+\delta )}}$ by setting $\lambda =\ln (1+\delta )$, which can be justified by taking derivatives of $\frac{e^{(e^{\lambda }-1)}}{e^{\lambda (1+\delta )}}$.

---

We then proceed to the lower tail, the probability that the random variable deviates below the mean value:

Chernoff bound (the lower tail)

Let $X=\sum _{i=1}^n{X}_i$, where $X_1,X_2,\dots ,X_n$ are independent Poisson trials. Let $\mu =\mathbf{E}[X]$. Then for any $0<\delta <1$, $Pr[X\le (1-\delta )\mu ]\le {\left(\frac{e^{-\delta }}{(1-\delta {)}^{(1-\delta )}}\right)}^{\mu }.$

Proof. For any $\lambda <0$, by the same analysis as in the upper tail version, $\begin{array}{rl}Pr[X\le (1-\delta )\mu ]& =Pr[e^{\lambda X}\ge e^{\lambda (1-\delta )\mu }]\\ & \le \frac{\mathbf{E}\left[e^{\lambda X}\right]}{e^{\lambda (1-\delta )\mu }}\\ & \le {\left(\frac{e^{(e^{\lambda }-1)}}{e^{\lambda (1-\delta )}}\right)}^{\mu }.\end{array}$ For any $0<\delta <1$, we can let $\lambda =\ln (1-\delta )<0$ to get $Pr[X\ge (1-\delta )\mu ]\le {\left(\frac{e^{-\delta }}{(1-\delta {)}^{(1-\delta )}}\right)}^{\mu }.$ $◻$

Useful forms of the Chernoff bounds

Some useful special forms of the bounds can be derived directly from the above general forms of the bounds. We now know better why we say that the bounds are exponentially sharp.

Useful forms of the Chernoff bound

Let $X=\sum _{i=1}^n{X}_i$, where $X_1,X_2,\dots ,X_n$ are independent Poisson trials. Let $\mu =\mathbf{E}[X]$. Then 1. for $0<\delta \le 1$, $Pr[X\ge (1+\delta )\mu ]<\exp (-\frac{\mu {\delta }^2}{3});$ $Pr[X\le (1-\delta )\mu ]<\exp (-\frac{\mu {\delta }^2}{2});$ 2. for $t\ge 2e\mu$, $Pr[X\ge t]\le 2^{-t}.$

Proof. To obtain the bounds in (1), we need to show that for $0<\delta <1$, $\frac{e^{\delta }}{(1+\delta {)}^{(1+\delta )}}\le e^{-{\delta }^2/3}$ and $\frac{e^{-\delta }}{(1-\delta {)}^{(1-\delta )}}\le e^{-{\delta }^2/2}$. We can verify both inequalities by standard analysis techniques. To obtain the bound in (2), let $t=(1+\delta )\mu$. Then $\delta =t/\mu -1\ge 2e-1$. Hence, $\begin{array}{rl}Pr[X\ge (1+\delta )\mu ]& \le {\left(\frac{e^{\delta }}{(1+\delta {)}^{(1+\delta )}}\right)}^{\mu }\\ & \le {\left(\frac{e}{1+\delta }\right)}^{(1+\delta )\mu }\\ & \le {\left(\frac{e}{2e}\right)}^t\\ & \le 2^{-t}\end{array}$ $◻$

Applications to balls-into-bins

Throwing $m$ balls uniformly and independently to $n$ bins, what is the maximum load of all bins with high probability? In the last class, we gave an analysis of this problem by using a counting argument.

Now we give a more "advanced" analysis by using Chernoff bounds.

For any $i\in [n]$ and $j\in [m]$, let $X_{ij}$ be the indicator variable for the event that ball $j$ is thrown to bin $i$. Obviously

$\mathbf{E}[X_{ij}]=Pr[\text{ball }j\text{ is thrown to bin }i]=\frac{1}{n}$

Let $Y_i=\sum _{j\in [m]}{X}_{ij}$ be the load of bin $i$.

Then the expected load of bin $i$ is

$(\ast )\mu =\mathbf{E}[Y_i]=\mathbf{E}\left[\sum _{j\in [m]}{X}_{ij}\right]=\sum _{j\in [m]}\mathbf{E}[X_{ij}]=m/n.$

For the case $m=n$, it holds that $\mu =1$

Note that $Y_i$ is a sum of $m$ mutually independent indicator variable. Applying Chernoff bound, for any particular bin $i\in [n]$,

$Pr[Y_i>(1+\delta )\mu ]\le {\left(\frac{e^{\delta }}{(1+\delta {)}^{1+\delta }}\right)}^{\mu }.$

The $m=n$ case

When $m=n$, $\mu =1$. Write $c=1+\delta$. The above bound can be written as

$Pr[Y_i>c]\le \frac{e^{c-1}}{c^c}.$

Let $c=\frac{e\ln n}{\ln \ln n}$, we evaluate $\frac{e^{c-1}}{c^c}$ by taking logarithm to its reciprocal.

$\begin{array}{rl}\ln \left(\frac{c^c}{e^{c-1}}\right)& =c\ln c-c+1\\ & =c(\ln c-1)+1\\ & =\frac{e\ln n}{\ln \ln n}(\ln \ln n-\ln \ln \ln n)+1\\ & \ge \frac{e\ln n}{\ln \ln n}\cdot \frac{2}{e}\ln \ln n+1\\ & \ge 2\ln n.\end{array}$

Thus,

$Pr[Y_i>\frac{e\ln n}{\ln \ln n}]\le \frac{1}{n^2}.$

Applying the union bound, the probability that there exists a bin with load $>12\ln n$ is

$n\cdot Pr[Y_1>\frac{e\ln n}{\ln \ln n}]\le \frac{1}{n}$.

Therefore, for $m=n$, with high probability, the maximum load is $O\left(\frac{e\ln n}{\ln \ln n}\right)$.

The $m>\ln n$ case

When $m\ge n\ln n$, then according to $(\ast )$, $\mu =\frac{m}{n}\ge \ln n$

We can apply an easier form of the Chernoff bounds,

$Pr[Y_i\ge 2e\mu ]\le 2^{-2e\mu }\le 2^{-2e\ln n}<\frac{1}{n^2}.$

By the union bound, the probability that there exists a bin with load $\ge 2e\frac{m}{n}$ is,

$n\cdot Pr[Y_1>2e\frac{m}{n}]=n\cdot Pr[Y_1>2e\mu ]\le \frac{1}{n}$.

Therefore, for $m\ge n\ln n$, with high probability, the maximum load is $O\left(\frac{m}{n}\right)$.

Martingales

"Martingale" originally refers to a betting strategy in which the gambler doubles his bet after every loss. Assuming unlimited wealth, this strategy is guaranteed to eventually have a positive net profit. For example, starting from an initial stake 1, after $n$ losses, if the $(n+1)$th bet wins, then it gives a net profit of

$2^n-\sum _{i=1}^n{2}^{i-1}=1,$

which is a positive number.

However, the assumption of unlimited wealth is unrealistic. For limited wealth, with geometrically increasing bet, it is very likely to end up bankrupt. You should never try this strategy in real life.

Suppose that the gambler is allowed to use any strategy. His stake on the next beting is decided based on the results of all the bettings so far. This gives us a highly dependent sequence of random variables $X_0,X_1,\dots ,$, where $X_0$ is his initial capital, and $X_i$ represents his capital after the $i$th betting. Up to different betting strategies, $X_i$ can be arbitrarily dependent on $X_0,\dots ,X_{i-1}$. However, as long as the game is fair, namely, winning and losing with equal chances, conditioning on the past variables $X_0,\dots ,X_{i-1}$, we will expect no change in the value of the present variable $X_i$ on average. Random variables satisfying this property is called a martingale sequence.

Definition (martingale)

A sequence of random variables $X_0,X_1,\dots$ is a martingale if for all $i>0$, $\begin{array}{r}\mathbf{E}[X_i\mid X_0,\dots ,X_{i-1}]=X_{i-1}.\end{array}$

The martingale can be generalized to be with respect to another sequence of random variables.

Definition (martingale, general version)

A sequence of random variables $Y_0,Y_1,\dots$ is a martingale with respect to the sequence $X_0,X_1,\dots$ if, for all $i\ge 0$, the following conditions hold: $Y_i$ is a function of $X_0,X_1,\dots ,X_i$; $\begin{array}{r}\mathbf{E}[Y_{i+1}\mid X_0,\dots ,X_i]=Y_i.\end{array}$

Therefore, a sequence $X_0,X_1,\dots$ is a martingale if it is a martingale with respect to itself.

The purpose of this generalization is that we are usually more interested in a function of a sequence of random variables, rather than the sequence itself.

Azuma's Inequality

The Azuma's inequality is a martingale tail inequality.

Azuma's Inequality

Let $X_0,X_1,\dots$ be a martingale such that, for all $k\ge 1$, $|X_k-X_{k-1}|\le c_k,$ Then $\begin{array}{r}Pr[|X_n-X_0|\ge t]\le 2\exp (-\frac{t^2}{2\sum _{k=1}^n{c}_k^2}).\end{array}$

Unlike the Chernoff bounds, there is no assumption of independence, which makes the martingale inequalities more useful.

The following bounded difference condition

$|X_k-X_{k-1}|\le c_k$

says that the martingale $X_0,X_1,\dots$ as a process evolving over time, never makes big change in a single step.

The Azuma's inequality says that for any martingale satisfying the bounded difference condition, it is unlikely that process wanders far from its starting point.

A special case is when the differences are bounded by a constant. The following corollary is directly implied by the Azuma's inequality.

Corollary

Let $X_0,X_1,\dots$ be a martingale such that, for all $k\ge 1$, $|X_k-X_{k-1}|\le c,$ Then $\begin{array}{r}Pr[|X_n-X_0|\ge ct\sqrt{n}]\le 2e^{-t^2/2}.\end{array}$

This corollary states that for any martingale sequence whose diferences are bounded by a constant, the probability that it deviates $\omega (\sqrt{n})$ far away from the starting point after $n$ steps is bounded by $o(1)$.

Generalization

Azuma's inequality can be generalized to a martingale with respect another sequence.

Azuma's Inequality (general version)

Let $Y_0,Y_1,\dots$ be a martingale with respect to the sequence $X_0,X_1,\dots$ such that, for all $k\ge 1$, $|Y_k-Y_{k-1}|\le c_k,$ Then $\begin{array}{r}Pr[|Y_n-Y_0|\ge t]\le 2\exp (-\frac{t^2}{2\sum _{k=1}^n{c}_k^2}).\end{array}$

The Proof of Azuma's Inueqality

We will only give the formal proof of the non-generalized version. The proof of the general version is almost identical, with the only difference that we work on random sequence $Y_i$ conditioning on sequence $X_i$.

The proof of Azuma's Inequality uses several ideas which are used in the proof of the Chernoff bounds. We first observe that the total deviation of the martingale sequence can be represented as the sum of deferences in every steps. Thus, as the Chernoff bounds, we are looking for a bound of the deviation of the sum of random variables. The strategy of the proof is almost the same as the proof of Chernoff bounds: we first apply Markov's inequality to the moment generating function, then we bound the moment generating function, and at last we optimize the parameter of the moment generating function. However, unlike the Chernoff bounds, the martingale differences are not independent any more. So we replace the use of the independence in the Chernoff bound by the martingale property. The proof is detailed as follows.

In order to bound the probability of $|X_n-X_0|\ge t$, we first bound the upper tail $Pr[X_n-X_0\ge t]$. The bound of the lower tail can be symmetrically proved with the $X_i$ replaced by $-X_i$.

Represent the deviation as the sum of differences

We define the martingale difference sequence: for $i\ge 1$, let

$Y_i=X_i-X_{i-1}.$

It holds that

$\begin{array}{rl}\mathbf{E}[Y_i\mid X_0,\dots ,X_{i-1}]& =\mathbf{E}[X_i-X_{i-1}\mid X_0,\dots ,X_{i-1}]\\ & =\mathbf{E}[X_i\mid X_0,\dots ,X_{i-1}]-\mathbf{E}[X_{i-1}\mid X_0,\dots ,X_{i-1}]\\ & =X_{i-1}-X_{i-1}\\ & =0.\end{array}$

The second to the last equation is due to the fact that $X_0,X_1,\dots$ is a martingale and the definition of conditional expectation.

Let $Z_n$ be the accumulated differences

$Z_n=\sum _{i=1}^n{Y}_i.$

The deviation $(X_n-X_0)$ can be computed by the accumulated differences:

$\begin{array}{rl}{X}_n-X_0& =(X_1-X_0)+(X_2-X_1)+\cdots +(X_n-X_{n-1})\\ & =\sum _{i=1}^n{Y}_i\\ & =Z_n.\end{array}$

We then only need to upper bound the probability of the event $Z_n\ge t$.

Apply Markov's inequality to the moment generating function

The event $Z_n\ge t$ is equivalent to that $e^{\lambda Z_n}\ge e^{\lambda t}$ for $\lambda >0$. Apply Markov's inequality, we have

$\begin{array}{rl}Pr[Z_n\ge t]& =Pr[e^{\lambda Z_n}\ge e^{\lambda t}]\\ & \le \frac{\mathbf{E}\left[e^{\lambda Z_n}\right]}{e^{\lambda t}}.\end{array}$

This is exactly the same as what we did to prove the Chernoff bound. Next, we need to bound the moment generating function $\mathbf{E}\left[e^{\lambda Z_n}\right]$.

Bound the moment generating functions

The moment generating function

$\begin{array}{rl}\mathbf{E}\left[e^{\lambda Z_n}\right]& =\mathbf{E}\left[\mathbf{E}[e^{\lambda Z_n}\mid X_0,\dots ,X_{n-1}]\right]\\ & =\mathbf{E}\left[\mathbf{E}[e^{\lambda (Z_{n-1}+Y_n)}\mid X_0,\dots ,X_{n-1}]\right]\\ & =\mathbf{E}\left[\mathbf{E}[e^{\lambda Z_{n-1}}\cdot e^{\lambda Y_n}\mid X_0,\dots ,X_{n-1}]\right]\\ & =\mathbf{E}[e^{\lambda Z_{n-1}}\cdot \mathbf{E}[e^{\lambda Y_n}\mid X_0,\dots ,X_{n-1}]]\end{array}$

The first and the last equations are due to the fundamental facts about conditional expectation which are proved by us in the first section.

We then upper bound the $\mathbf{E}[e^{\lambda Y_n}\mid X_0,\dots ,X_{n-1}]$ by a constant. To do so, we need the following technical lemma which is proved by the convexity of $e^{\lambda Y_n}$.

Lemma

Let $X$ be a random variable such that $\mathbf{E}[X]=0$ and $|X|\le c$. Then for $\lambda >0$, $\mathbf{E}[e^{\lambda X}]\le e^{{\lambda }^2{c}^2/2}.$

Proof. Observe that for $\lambda >0$, the function $e^{\lambda X}$ of the variable $X$ is convex in the interval $[-c,c]$. We draw a line between the two endpoints points $(-c,e^{-\lambda c})$ and $(c,e^{\lambda c})$. The curve of $e^{\lambda X}$ lies entirely below this line. Thus, $\begin{array}{rl}{e}^{\lambda X}& \le \frac{c-X}{2c}{e}^{-\lambda c}+\frac{c+X}{2c}{e}^{\lambda c}\\ & =\frac{e^{\lambda c}+e^{-\lambda c}}{2}+\frac{X}{2c}(e^{\lambda c}-e^{-\lambda c}).\end{array}$ Since $\mathbf{E}[X]=0$, we have $\begin{array}{rl}\mathbf{E}[e^{\lambda X}]& \le \mathbf{E}[\frac{e^{\lambda c}+e^{-\lambda c}}{2}+\frac{X}{2c}(e^{\lambda c}-e^{-\lambda c})]\\ & =\frac{e^{\lambda c}+e^{-\lambda c}}{2}+\frac{e^{\lambda c}-e^{-\lambda c}}{2c}\mathbf{E}[X]\\ & =\frac{e^{\lambda c}+e^{-\lambda c}}{2}.\end{array}$ By expanding both sides as Taylor's series, it can be verified that $\frac{e^{\lambda c}+e^{-\lambda c}}{2}\le e^{{\lambda }^2{c}^2/2}$. $◻$

Apply the above lemma to the random variable

$(Y_n\mid X_0,\dots ,X_{n-1})$

We have already shown that its expectation $\mathbf{E}[(Y_n\mid X_0,\dots ,X_{n-1})]=0,$ and by the bounded difference condition of Azuma's inequality, we have $|Y_n|=|(X_n-X_{n-1})|\le c_n.$ Thus, due to the above lemma, it holds that

$\mathbf{E}[e^{\lambda Y_n}\mid X_0,\dots ,X_{n-1}]\le e^{{\lambda }^2{c}_n^2/2}.$

Back to our analysis of the expectation $\mathbf{E}\left[e^{\lambda Z_n}\right]$, we have

$\begin{array}{rl}\mathbf{E}\left[e^{\lambda Z_n}\right]& =\mathbf{E}[e^{\lambda Z_{n-1}}\cdot \mathbf{E}[e^{\lambda Y_n}\mid X_0,\dots ,X_{n-1}]]\\ & \le \mathbf{E}[e^{\lambda Z_{n-1}}\cdot e^{{\lambda }^2{c}_n^2/2}]\\ & =e^{{\lambda }^2{c}_n^2/2}\cdot \mathbf{E}\left[e^{\lambda Z_{n-1}}\right].\end{array}$

Apply the same analysis to $\mathbf{E}\left[e^{\lambda Z_{n-1}}\right]$, we can solve the above recursion by

$\begin{array}{rl}\mathbf{E}\left[e^{\lambda Z_n}\right]& \le \prod _{k=1}^n{e}^{{\lambda }^2{c}_k^2/2}\\ & =\exp \left({\lambda }^2\sum _{k=1}^n{c}_k^2/2\right).\end{array}$

Go back to the Markov's inequality,

$\begin{array}{rl}Pr[Z_n\ge t]& \le \frac{\mathbf{E}\left[e^{\lambda Z_n}\right]}{e^{\lambda t}}\\ & \le \exp ({\lambda }^2\sum _{k=1}^n{c}_k^2/2-\lambda t).\end{array}$

We then only need to choose a proper $\lambda >0$.

Optimization

By choosing $\lambda =\frac{t}{\sum _{k=1}^n{c}_k^2}$, we have that

$\exp ({\lambda }^2\sum _{k=1}^n{c}_k^2/2-\lambda t)=\exp (-\frac{t^2}{2\sum _{k=1}^n{c}_k^2}).$

Thus, the probability

$\begin{array}{rl}Pr[X_n-X_0\ge t]& =Pr[Z_n\ge t]\\ & \le \exp ({\lambda }^2\sum _{k=1}^n{c}_k^2/2-\lambda t)\\ & =\exp (-\frac{t^2}{2\sum _{k=1}^n{c}_k^2}).\end{array}$

The upper tail of Azuma's inequality is proved. By replacing $X_i$ by $-X_i$, the lower tail can be treated just as the upper tail. Applying the union bound, Azuma's inequality is proved.

The Doob martingales

The following definition describes a very general approach for constructing an important type of martingales.

Definition (The Doob sequence)

The Doob sequence of a function $f$ with respect to a sequence of random variables $X_1,\dots ,X_n$ is defined by $Y_i=\mathbf{E}[f(X_1,\dots ,X_n)\mid X_1,\dots ,X_i],0\le i\le n.$ In particular, $Y_0=\mathbf{E}[f(X_1,\dots ,X_n)]$ and $Y_n=f(X_1,\dots ,X_n)$.

The Doob sequence of a function defines a martingale. That is

$\mathbf{E}[Y_i\mid X_1,\dots ,X_{i-1}]=Y_{i-1},$

for any $0\le i\le n$.

To prove this claim, we recall the definition that $Y_i=\mathbf{E}[f(X_1,\dots ,X_n)\mid X_1,\dots ,X_i]$, thus,

$\begin{array}{rl}\mathbf{E}[Y_i\mid X_1,\dots ,X_{i-1}]& =\mathbf{E}[\mathbf{E}[f(X_1,\dots ,X_n)\mid X_1,\dots ,X_i]\mid X_1,\dots ,X_{i-1}]\\ & =\mathbf{E}[f(X_1,\dots ,X_n)\mid X_1,\dots ,X_{i-1}]\\ & =Y_{i-1},\end{array}$

where the second equation is due to the fundamental fact about conditional expectation introduced in the first section.

The Doob martingale describes a very natural procedure to determine a function value of a sequence of random variables. Suppose that we want to predict the value of a function $f(X_1,\dots ,X_n)$ of random variables $X_1,\dots ,X_n$. The Doob sequence $Y_0,Y_1,\dots ,Y_n$ represents a sequence of refined estimates of the value of $f(X_1,\dots ,X_n)$, gradually using more information on the values of the random variables $X_1,\dots ,X_n$. The first element $Y_0$ is just the expectation of $f(X_1,\dots ,X_n)$. Element $Y_i$ is the expected value of $f(X_1,\dots ,X_n)$ when the values of $X_1,\dots ,X_i$ are known, and $Y_n=f(X_1,\dots ,X_n)$ when $f(X_1,\dots ,X_n)$ is fully determined by $X_1,\dots ,X_n$.

The following two Doob martingales arise in evaluating the parameters of random graphs.

edge exposure martingale

Let $G$ be a random graph on $n$ vertices. Let $f$ be a real-valued function of graphs, such as, chromatic number, number of triangles, the size of the largest clique or independent set, etc. Denote that $m=(\genfrac{}{}{0ex}{}{n}{2})$. Fix an arbitrary numbering of potential edges between the $n$ vertices, and denote the edges as $e_1,\dots ,e_m$. Let

$X_i=\{\begin{array}{ll}1& \text{if }{e}_i\in G,\\ 0& \text{otherwise}.\end{array}$

Let $Y_0=\mathbf{E}[f(G)]$ and for $i=1,\dots ,m$, let $Y_i=\mathbf{E}[f(G)\mid X_1,\dots ,X_i]$.

The sequence $Y_0,Y_1,\dots ,Y_n$ gives a Doob martingale that is commonly called the edge exposure martingale.

vertex exposure martingale

Instead of revealing edges one at a time, we could reveal the set of edges connected to a given vertex, one vertex at a time. Suppose that the vertex set is $[n]$. Let $X_i$ be the subgraph of $G$ induced by the vertex set $[i]$, i.e. the first $i$ vertices.

Let $Y_0=\mathbf{E}[f(G)]$ and for $i=1,\dots ,n$, let $Y_i=\mathbf{E}[f(G)\mid X_1,\dots ,X_i]$.

The sequence $Y_0,Y_1,\dots ,Y_n$ gives a Doob martingale that is commonly called the vertex exposure martingale.

Chromatic number

The random graph $G(n,p)$ is the graph on $n$ vertices $[n]$, obtained by selecting each pair of vertices to be an edge, randomly and independently, with probability $p$. We denote $G\sim G(n,p)$ if $G$ is generated in this way.

Theorem [Shamir and Spencer (1987)]

Let $G\sim G(n,p)$. Let $\chi (G)$ be the chromatic number of $G$. Then $\begin{array}{r}Pr[|\chi (G)-\mathbf{E}[\chi (G)]|\ge t\sqrt{n}]\le 2e^{-t^2/2}.\end{array}$

Proof. Consider the vertex exposure martingale $Y_i=\mathbf{E}[\chi (G)\mid X_1,\dots ,X_i]$ where each $X_k$ exposes the induced subgraph of $G$ on vertex set $[k]$. A single vertex can always be given a new color so that the graph is properly colored, thus the bounded difference condition $|Y_i-Y_{i-1}|\le 1$ is satisfied. Now apply the Azuma's inequality for the martingale $Y_1,\dots ,Y_n$ with respect to $X_1,\dots ,X_n$. $◻$

For $t=\omega (1)$, the theorem states that the chromatic number of a random graph is tightly concentrated around its mean. The proof gives no clue as to where the mean is. This actually shows how powerful the martingale inequalities are: we can prove that a distribution is concentrated to its expectation without actually knowing the expectation.

Hoeffding's Inequality

The following theorem states the so-called Hoeffding's inequality. It is a generalized version of the Chernoff bounds. Recall that the Chernoff bounds hold for the sum of independent trials. When the random variables are not trials, the Hoeffding's inequality is useful, since it holds for the sum of any independent random variables whose ranges are bounded.

Hoeffding's inequality

Let $X=\sum _{i=1}^n{X}_i$, where $X_1,\dots ,X_n$ are independent random variables with $a_i\le X_i\le b_i$ for each $1\le i\le n$. Let $\mu =\mathbf{E}[X]$. Then $Pr[|X-\mu |\ge t]\le 2\exp (-\frac{t^2}{2\sum _{i=1}^n(b_i-a_i{)}^2}).$

Proof. Define the Doob martingale sequence $Y_i=\mathbf{E}[\sum _{j=1}^n{X}_j|X_1,\dots ,X_i]$. Obviously $Y_0=\mu$ and $Y_n=X$. $\begin{array}{rl}|Y_i-Y_{i-1}|& =|\mathbf{E}[\sum _{j=1}^n{X}_j|X_0,\dots ,X_i]-\mathbf{E}[\sum _{j=1}^n{X}_j|X_0,\dots ,X_{i-1}]|\\ & =|\sum _{j=1}^i{X}_i+\sum _{j=i+1}^n\mathbf{E}[X_j]-\sum _{j=1}^{i-1}{X}_i-\sum _{j=i}^n\mathbf{E}[X_j]|\\ & =|X_i-\mathbf{E}[X_i]|\\ & \le b_i-a_i\end{array}$ Apply Azuma's inequality for the martingale $Y_0,\dots ,Y_n$ with respect to $X_1,\dots ,X_n$, the Hoeffding's inequality is proved. $◻$

The Bounded Difference Method

Combining Azuma's inequality with the construction of Doob martingales, we have the powerful Bounded Difference Method for concentration of measures.

For arbitrary random variables

Given a sequence of random variables $X_1,\dots ,X_n$ and a function $f$. The Doob sequence constructs a martingale from them. Combining this construction with Azuma's inequality, we can get a very powerful theorem called "the method of averaged bounded differences" which bounds the concentration for arbitrary function on arbitrary random variables (not necessarily a martingale).

Theorem (Method of averaged bounded differences)

Let $\mathit{X}=(X_1,\dots ,X_n)$ be arbitrary random variables and let $f$ be a function of $X_0,X_1,\dots ,X_n$ satisfying that, for all $1\le i\le n$, $|\mathbf{E}[f(\mathit{X})\mid X_1,\dots ,X_i]-\mathbf{E}[f(\mathit{X})\mid X_1,\dots ,X_{i-1}]|\le c_i,$ Then $\begin{array}{r}Pr[|f(\mathit{X})-\mathbf{E}[f(\mathit{X})]|\ge t]\le 2\exp (-\frac{t^2}{2\sum _{i=1}^n{c}_i^2}).\end{array}$

Proof. Define the Doob Martingale sequence $Y_0,Y_1,\dots ,Y_n$ by setting $Y_0=\mathbf{E}[f(X_1,\dots ,X_n)]$ and, for $1\le i\le n$, $Y_i=\mathbf{E}[f(X_1,\dots ,X_n)\mid X_1,\dots ,X_i]$. Then the above theorem is a restatement of the Azuma's inequality holding for $Y_0,Y_1,\dots ,Y_n$. $◻$

For independent random variables

The condition of bounded averaged differences is usually hard to check. This severely limits the usefulness of the method. To overcome this, we introduce a property which is much easier to check, called the Lipschitz condition.

Definition (Lipschitz condition)

A function $f(x_1,\dots ,x_n)$ satisfies the Lipschitz condition, if for any $x_1,\dots ,x_n$ and any $y_i$, $\begin{array}{r}|f(x_1,\dots ,x_{i-1},x_i,x_{i+1},\dots ,x_n)-f(x_1,\dots ,x_{i-1},y_i,x_{i+1},\dots ,x_n)|\le 1.\end{array}$

In other words, the function satisfies the Lipschitz condition if an arbitrary change in the value of any one argument does not change the value of the function by more than 1.

The diference of 1 can be replaced by arbitrary constants, which gives a generalized version of Lipschitz condition.

Definition (Lipschitz condition, general version)

A function $f(x_1,\dots ,x_n)$ satisfies the Lipschitz condition with constants $c_i$, $1\le i\le n$, if for any $x_1,\dots ,x_n$ and any $y_i$, $\begin{array}{r}|f(x_1,\dots ,x_{i-1},x_i,x_{i+1},\dots ,x_n)-f(x_1,\dots ,x_{i-1},y_i,x_{i+1},\dots ,x_n)|\le c_i.\end{array}$

The following "method of bounded differences" can be developed for functions satisfying the Lipschitz condition. Unfortunately, in order to imply the condition of averaged bounded differences from the Lipschitz condition, we have to restrict the method to independent random variables.

Corollary (Method of bounded differences)

Let $\mathit{X}=(X_1,\dots ,X_n)$ be $n$ independent random variables and let $f$ be a function satisfying the Lipschitz condition with constants $c_i$, $1\le i\le n$. Then $\begin{array}{r}Pr[|f(\mathit{X})-\mathbf{E}[f(\mathit{X})]|\ge t]\le 2\exp (-\frac{t^2}{2\sum _{i=1}^n{c}_i^2}).\end{array}$

Proof. For convenience, we denote that ${\mathit{X}}_{[i,j]}=(X_i,X_{i+1},\dots ,X_j)$ for any $1\le i\le j\le n$. We first show that the Lipschitz condition with constants $c_i$, $1\le i\le n$, implies another condition called the averaged Lipschitz condition (ALC): for any $a_i,b_i$, $1\le i\le n$, $|\mathbf{E}[f(\mathit{X})\mid {\mathit{X}}_{[1,i-1]},X_i=a_i]-\mathbf{E}[f(\mathit{X})\mid {\mathit{X}}_{[1,i-1]},X_i=b_i]|\le c_i.$ And this condition implies the averaged bounded difference condition: for all $1\le i\le n$, $|\mathbf{E}[f(\mathit{X})\mid {\mathit{X}}_{[1,i]}]-\mathbf{E}[f(\mathit{X})\mid {\mathit{X}}_{[1,i-1]}]|\le c_i.$ Then by applying the method of averaged bounded differences, the corollary can be proved. For any $a$, by the law of total expectation, $\begin{array}{rl}& \mathbf{E}[f(\mathit{X})\mid {\mathit{X}}_{[1,i-1]},X_i=a]\\ & =\sum _{a_{i+1},\dots ,a_n}\mathbf{E}[f(\mathit{X})\mid {\mathit{X}}_{[1,i-1]},X_i=a,{\mathit{X}}_{[i+1,n]}={\mathit{a}}_{[i+1,n]}]\cdot Pr[{\mathit{X}}_{[i+1,n]}={\mathit{a}}_{[i+1,n]}\mid {\mathit{X}}_{[1,i-1]},X_i=a]\\ & =\sum _{a_{i+1},\dots ,a_n}\mathbf{E}[f(\mathit{X})\mid {\mathit{X}}_{[1,i-1]},X_i=a,{\mathit{X}}_{[i+1,n]}={\mathit{a}}_{[i+1,n]}]\cdot Pr[{\mathit{X}}_{[i+1,n]}={\mathit{a}}_{[i+1,n]}](\text{independence})\\ & =\sum _{a_{i+1},\dots ,a_n}f({\mathit{X}}_{[1,i-1]},a,{\mathit{a}}_{[i+1,n]})\cdot Pr[{\mathit{X}}_{[i+1,n]}={\mathit{a}}_{[i+1,n]}].\end{array}$ Let $a=a_i$ and $b_i$, and take the diference. Then $\begin{array}{rl}& |\mathbf{E}[f(\mathit{X})\mid {\mathit{X}}_{[1,i-1]},X_i=a_i]-\mathbf{E}[f(\mathit{X})\mid {\mathit{X}}_{[1,i-1]},X_i=b_i]|\\ & =|\sum _{a_{i+1},\dots ,a_n}(f({\mathit{X}}_{[1,i-1]},a_i,{\mathit{a}}_{[i+1,n]})-f({\mathit{X}}_{[1,i-1]},b_i,{\mathit{a}}_{[i+1,n]}))Pr[{\mathit{X}}_{[i+1,n]}={\mathit{a}}_{[i+1,n]}]|\\ & \le \sum _{a_{i+1},\dots ,a_n}|f({\mathit{X}}_{[1,i-1]},a_i,{\mathit{a}}_{[i+1,n]})-f({\mathit{X}}_{[1,i-1]},b_i,{\mathit{a}}_{[i+1,n]})|Pr[{\mathit{X}}_{[i+1,n]}={\mathit{a}}_{[i+1,n]}]\\ & \le \sum _{a_{i+1},\dots ,a_n}{c}_{i}Pr[{\mathit{X}}_{[i+1,n]}={\mathit{a}}_{[i+1,n]}](\text{Lipschitz condition})\\ & =c_i.\end{array}$ Thus, the Lipschitz condition is transformed to the ALC. We then deduce the averaged bounded difference condition from ALC. By the law of total expectation, $\mathbf{E}[f(\mathit{X})\mid {\mathit{X}}_{[1,i-1]}]=\sum _a\mathbf{E}[f(\mathit{X})\mid {\mathit{X}}_{[1,i-1]},X_i=a]\cdot Pr[X_i=a\mid {\mathit{X}}_{[1,i-1]}].$ We can trivially write $\mathbf{E}[f(\mathit{X})\mid {\mathit{X}}_{[1,i]}]$ as $\mathbf{E}[f(\mathit{X})\mid {\mathit{X}}_{[1,i]}]=\sum _a\mathbf{E}[f(\mathit{X})\mid {\mathit{X}}_{[1,i]}]\cdot Pr[X_i=a\mid {\mathit{X}}_{[1,i-1]}].$ Hence, the difference is $\begin{array}{rl}& |\mathbf{E}[f(\mathit{X})\mid {\mathit{X}}_{[1,i]}]-\mathbf{E}[f(\mathit{X})\mid {\mathit{X}}_{[1,i-1]}]|\\ & =|\sum _a(\mathbf{E}[f(\mathit{X})\mid {\mathit{X}}_{[1,i]}]-\mathbf{E}[f(\mathit{X})\mid {\mathit{X}}_{[1,i-1]},X_i=a])\cdot Pr[X_i=a\mid {\mathit{X}}_{[1,i-1]}]|\\ & \le \sum _a|\mathbf{E}[f(\mathit{X})\mid {\mathit{X}}_{[1,i]}]-\mathbf{E}[f(\mathit{X})\mid {\mathit{X}}_{[1,i-1]},X_i=a]|\cdot Pr[X_i=a\mid {\mathit{X}}_{[1,i-1]}]\\ & \le \sum _a{c}_{i}Pr[X_i=a\mid {\mathit{X}}_{[1,i-1]}](\text{due to ALC})\\ & =c_i.\end{array}$ The averaged bounded diference condition is implied. Applying the method of averaged bounded diferences, the corollary follows. $◻$

Applications

Occupancy problem

Throwing $m$ balls uniformly and independently at random to $n$ bins, we ask for the occupancies of bins by the balls. In particular, we are interested in the number of empty bins.

This problem can be described equivalently as follows. Let $f:[m]\to [n]$ be a uniform random function from $[m]\to [n]$. We ask for the number of $i\in [n]$ that $f^{-1}(i)$ is empty.

For any $i\in [n]$, let $X_i$ indicate the emptiness of bin $i$. Let $X=\sum _{i=1}^n{X}_i$ be the number of empty bins.

$\mathbf{E}[X_i]=Pr[\text{bin }i\text{ is empty}]={(1-\frac{1}{n})}^m.$

By the linearity of expectation,

$\mathbf{E}[X]=\sum _{i=1}^n\mathbf{E}[X_i]=n{(1-\frac{1}{n})}^m.$

We want to know how $X$ deviates from this expectation. The complication here is that $X_i$ are not independent. So we alternatively look at a sequence of independent random variables $Y_1,\dots ,Y_m$, where $Y_j\in [n]$ represents the bin into which the $j$th ball falls. Clearly $X$ is function of $Y_1,\dots ,Y_m$.

We than observe that changing the value of any $Y_i$ can change the value of $X$ by at most 1, because one ball can affect the emptiness of at most one bin. Thus as a function of independent random variables $Y_1,\dots ,Y_m$, $X$ satisfies the Lipschitz condition. Apply the method of bounded differences, it holds that

$Pr[|X-n{(1-\frac{1}{n})}^m|\ge t\sqrt{m}]=Pr[|X-\mathbf{E}[X]|\ge t\sqrt{m}]\le 2e^{-t^2/2}$

Thus, for sufficiently large $n$ and $m$, the number of empty bins is tightly concentrated around $n{(1-\frac{1}{n})}^m\approx \frac{n}{e^{m/n}}$

Pattern Matching

Let $\mathit{X}=(X_1,\dots ,X_n)$ be a sequence of characters chosen independently and uniformly at random from an alphabet $\mathrm{\Sigma }$, where $m=|\mathrm{\Sigma }|$. Let $\pi \in {\mathrm{\Sigma }}^k$ be an arbitrarily fixed string of $k$ characters from $\mathrm{\Sigma }$, called a pattern. Let $Y$ be the number of occurrences of the pattern $\pi$ as a substring of the random string $X$.

By the linearity of expectation, it is obvious that

$\mathbf{E}[Y]=(n-k+1){\left(\frac{1}{m}\right)}^k.$

We now look at the concentration of $Y$. The complication again lies in the dependencies between the matches. Yet we will see that $Y$ is well tightly concentrated around its expectation if $k$ is relatively small compared to $n$.

For a fixed pattern $\pi$, the random variable $Y$ is a function of the independent random variables $(X_1,\dots ,X_n)$. Any character $X_i$ participates in no more than $k$ matches, thus changing the value of any $X_i$ can affect the value of $Y$ by at most $k$. $Y$ satisfies the Lipschitz condition with constant $k$. Apply the method of bounded differences,

$Pr[|Y-\frac{n-k+1}{m^k}|\ge tk\sqrt{n}]=Pr[|Y-\mathbf{E}[Y]|\ge tk\sqrt{n}]\le 2e^{-t^2/2}$

Combining unit vectors

Let $u_1,\dots ,u_n$ be $n$ unit vectors from some normed space. That is, $\parallel u_i\parallel =1$ for any $1\le i\le n$, where $\parallel \cdot \parallel$ denote the vector norm (e.g. ${\ell }_1,{\ell }_2,{\ell }_{\mathrm{\infty }}$) of the space.

Let ${ϵ}_1,\dots ,{ϵ}_n\in \{-1,+1\}$ be independently chosen and $Pr[{ϵ}_i=-1]=Pr[{ϵ}_i=1]=1/2$.

Let

$v={ϵ}_1{u}_1+\cdots +{ϵ}_n{u}_n,$

and

$X=\parallel v\parallel .$

This kind of construction is very useful in combinatorial proofs of metric problems. We will show that by this construction, the random variable $X$ is well concentrated around its mean.

$X$ is a function of independent random variables ${ϵ}_1,\dots ,{ϵ}_n$. By the triangle inequality for norms, it is easy to verify that changing the sign of a unit vector $u_i$ can only change the value of $X$ for at most 2, thus $X$ satisfies the Lipschitz condition with constant 2. The concentration result follows by applying the method of bounded differences:

$Pr[|X-\mathbf{E}[X]|\ge 2t\sqrt{n}]\le 2e^{-t^2/2}.$