概率论与数理统计 (Spring 2024)/Karger's min-cut algorithm: Difference between revisions

Latest revision as of 14:44, 19 March 2024

令 [math]\displaystyle{ G(V, E) }[/math] 是一个无向图。我们称边集 [math]\displaystyle{ C\subseteq E }[/math] 是图 [math]\displaystyle{ G }[/math] 的一个割，如果图 [math]\displaystyle{ G }[/math] 在删除所有 [math]\displaystyle{ C }[/math] 中的边后变得不连通。

最小割问题, 也称为全局最小割问题, 定义如下。

全局最小割问题

输入：无向图 [math]\displaystyle{ G(V,E) }[/math]；
输出：图 [math]\displaystyle{ G }[/math] 中具有最小 [math]\displaystyle{ |C| }[/math] 的割 [math]\displaystyle{ C }[/math]。

等价地，该问题要求找到一个将 [math]\displaystyle{ V }[/math] 分成两个不相交非空子集 [math]\displaystyle{ S }[/math] 和 [math]\displaystyle{ T }[/math] 的划分，使得跨越 [math]\displaystyle{ S }[/math] 和 [math]\displaystyle{ T }[/math] 的边总数最小。

我们考虑如下更具一般性的情境：输入图 [math]\displaystyle{ G }[/math] 可以是多重图（multigraph），这意味着任意两个顶点 [math]\displaystyle{ u }[/math] 和 [math]\displaystyle{ v }[/math] 之间可能存在多条平行边（parallel edges），也称为重(读音chóng)边。多重图中的割的定义与之前相同，割 [math]\displaystyle{ C }[/math] 的大小则由 [math]\displaystyle{ C }[/math] 中所有边（包括平行边）的总数给出。等价地，可以将多重图视为带有整数边权重的图，割 [math]\displaystyle{ C }[/math] 的大小表示为 [math]\displaystyle{ C }[/math] 中所有边的总权重。

通过最大流-最小割定理，可以得到这个问题的一个经典的确定性算法。最大流算法可以找到一个最小的[math]\displaystyle{ s }[/math]-[math]\displaystyle{ t }[/math]割, 将由输入任意指定的一个源点 [math]\displaystyle{ s\in V }[/math] 和一个汇点 [math]\displaystyle{ t\in V }[/math] 分割开来。然后可以通过穷举来找到针对任意固定源点 [math]\displaystyle{ s }[/math] 和所有可能的汇点 [math]\displaystyle{ t\neq s }[/math] 的最小 [math]\displaystyle{ s }[/math]-[math]\displaystyle{ t }[/math] 割，从而求得全局最小割。

Karger算法

我们将描述一个简洁优美的随机化算法来解决最小割问题。该算法最初是由David Karger提出的。

给定一个多重图 [math]\displaystyle{ G(V,E) }[/math] 和一条边 [math]\displaystyle{ e\in E }[/math]，我们定义如下的收缩操作 [math]\displaystyle{ \mathsf{Contract}(G,e) }[/math]，将 [math]\displaystyle{ G }[/math] 更新为一个新的多重图。

收缩算子 [math]\displaystyle{ \mathsf{Contract}(G,e) }[/math]

设 [math]\displaystyle{ e=\{u,v\} }[/math]：

将顶点 [math]\displaystyle{ u,v }[/math] 替换为一个新顶点 [math]\displaystyle{ x }[/math]；
对于图中任何一条连接 [math]\displaystyle{ u,v }[/math] 其中之一到 [math]\displaystyle{ u,v }[/math] 以外某顶点 [math]\displaystyle{ w\in V\setminus\{u,v\} }[/math] 的边，用一条新边 [math]\displaystyle{ \{x,w\} }[/math] 替换它；
图中剩余的部分保持不变。

换言之，[math]\displaystyle{ \mathsf{Contract}(G,\{u,v\}) }[/math] 将两个顶点 [math]\displaystyle{ u }[/math] 和 [math]\displaystyle{ v }[/math] 合并成一个新顶点 [math]\displaystyle{ x }[/math]，该新顶点邻接的边保留了原始图 [math]\displaystyle{ G }[/math] 中与 [math]\displaystyle{ u,v }[/math] 两顶点之一邻接的边（但不包括二者之间的平行边 [math]\displaystyle{ \{u,v\} }[/math]）。现在我们应该能意识到为什么我们考虑多重图而不是简单图——因为即使我们从没有平行边的简单图开始，收缩操作也可能引入平行边。

收缩操作的效果如图所示：

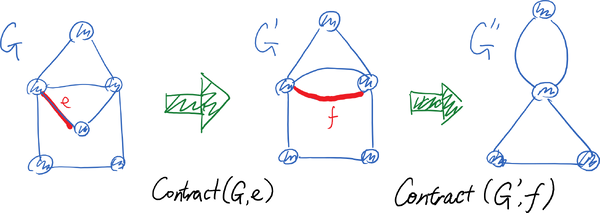
Karger算法的想法很简单：在每一步中，随机选择当前多重图中的一条边，将其收缩；重复这一操作，直至图中只剩下两个顶点——这两个剩下的顶点之间的所有边的集合，必然是最初图（乃至每一步中的图）中的一个割。

收缩算法 (Karger 1993)

输入: 多重图 [math]\displaystyle{ G(V,E) }[/math];

while [math]\displaystyle{ |V|\gt 2 }[/math] do

从当前图中均匀分布地选择一条随机的边 [math]\displaystyle{ e\in E }[/math];
[math]\displaystyle{ G=\mathsf{Contract}(G,e) }[/math];

return [math]\displaystyle{ C=E }[/math] (即当前所剩的最后两个顶点之间所有的平行边);

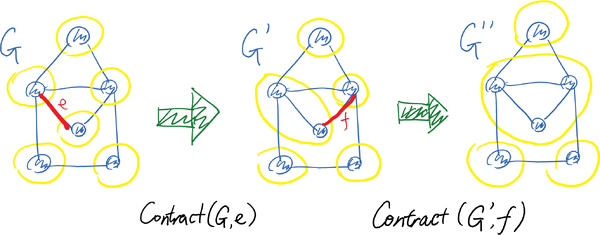
另一种看待收缩操作 [math]\displaystyle{ \mathsf{Contract}(G,e) }[/math] 的方式是将其解读为对两个顶点的等价类的合并。假设 [math]\displaystyle{ V={v_1,v_2,\ldots,v_n} }[/math] 是所有顶点的集合。我们从 [math]\displaystyle{ n }[/math] 个顶点等价类 [math]\displaystyle{ S_1,S_2,\ldots, S_n }[/math] 开始，其中每个等价类 [math]\displaystyle{ S_i={v_i} }[/math] 包含一个顶点。通过调用 [math]\displaystyle{ \mathsf{Contract}(G,e) }[/math]，其中 [math]\displaystyle{ e }[/math] 跨越了两个不同的等价类 [math]\displaystyle{ S_i }[/math] 和 [math]\displaystyle{ S_j }[/math]，其效果是将等价类 [math]\displaystyle{ S_i }[/math] 和 [math]\displaystyle{ S_j }[/math] 合并。收缩后的多重图中的边就是跨越不同顶点等价类之间的边。这一视角的效果如图所示：

Karger算法的分析

假设输入图 [math]\displaystyle{ G }[/math] 为一任意给定的多重图。Karger算法输出了该图的一个随机的割。我们需要分析该随机割是最小割的概率，即如下概率的下界：

[math]\displaystyle{ \Pr[\,\text{收缩算法输出了 }G\text{ 的一个最小割}\,] }[/math].

对此，我们证明如下更强的结论。令 [math]\displaystyle{ C }[/math] 是输入图 [math]\displaystyle{ G }[/math] 中的某个特定的最小割。我们将分析如下概率的下界：

[math]\displaystyle{ \Pr[\,\text{收缩算法输出了 }C\,] }[/math].

显然这一概率是收缩算法成功输出最小割的概率的下界（在这里我们使用了如下概率法则：对任意事件 [math]\displaystyle{ A }[/math] 和 [math]\displaystyle{ B }[/math]，若 [math]\displaystyle{ A\subseteq B }[/math]，则[math]\displaystyle{ \Pr(A)\le \Pr(B) }[/math]）。

我们引入以下记号：

令 [math]\displaystyle{ e_1,e_2,\ldots,e_{n-2} }[/math] 表示在运行收缩算法时，依次选中进行收缩的随机边的序列；
令 [math]\displaystyle{ G_1=G }[/math] 表示最初输入的多重图。对于 [math]\displaystyle{ i=1,2,\ldots,n-2 }[/math]，令 [math]\displaystyle{ G_{i+1}=\mathsf{Contract}(G_{i},e_i) }[/math] 表示第 [math]\displaystyle{ i }[/math] 轮收缩后的多重图。

我们可以做出如下的观察：

引理 1

如果 [math]\displaystyle{ C }[/math] 是多重图 [math]\displaystyle{ G }[/math] 中的一个最小割，且 [math]\displaystyle{ e\not\in C }[/math]，那么 [math]\displaystyle{ C }[/math] 在收缩图 [math]\displaystyle{ G'=\mathsf{Contract}(G,e) }[/math] 中仍然是一个最小割。

Proof.

我们首先观察到，收缩永远不会创建新的割：收缩图 [math]\displaystyle{ G' }[/math] 中的每个割也必定是原图 [math]\displaystyle{ G }[/math] 中的一个割。

然后我们观察到，原始图 [math]\displaystyle{ G }[/math] 中的割 [math]\displaystyle{ C }[/math] 能在收缩图 [math]\displaystyle{ G' }[/math] 中幸存，当且仅当收缩边 [math]\displaystyle{ e\not\in C }[/math]。

这两个观察都很容易通过收缩操作的定义进行验证（特别是在考虑顶点等价类的解释时更容易验证）。

[math]\displaystyle{ \square }[/math]

根据引理1，我们有：

[math]\displaystyle{ \Pr[\,\text{收缩算法输出了 }C\,]=\Pr[\,e_1,e_2,\ldots,e_{n-2}\not\in C\,] }[/math];

再根据链式法则，这一概率可被计算如下：

[math]\displaystyle{ \Pr[\,e_1,e_2,\ldots,e_{n-2}\not\in C\,]=\prod_{i=1}^{n-2}\Pr[\,e_i\not\in C\mid e_1,e_2,\ldots,e_{i-1}\not\in C\,] }[/math].

接下来我们的任务是对每个条件概率 [math]\displaystyle{ \Pr[\,e_i\not\in C\mid e_1,e_2,\ldots,e_{i-1}\not\in C\,] }[/math] 给出下界。注意到：根据引理1，条件 [math]\displaystyle{ e_1,e_2,\ldots,e_{i-1}\not\in C }[/math] 的发生意味着 [math]\displaystyle{ C }[/math] 仍是当前图 [math]\displaystyle{ G_i }[/math] 中的最小割；而 [math]\displaystyle{ e_i }[/math] 是图 [math]\displaystyle{ G_i }[/math] 中的一条均匀分布的随机边。于是条件概率 [math]\displaystyle{ \Pr[\,e_i\not\in C\mid e_1,e_2,\ldots,e_{i-1}\not\in C\,] }[/math] 即为图 [math]\displaystyle{ G_i }[/math] 中一条均匀随机边未命中其某个最小割 [math]\displaystyle{ C }[/math] 的概率。直观上：“最小”割应该在边集中相对稀疏，因此这一概率应该有下界。如下引理严格印证了这一直觉。

引理 2

如果 [math]\displaystyle{ C }[/math] 是多重图 [math]\displaystyle{ G(V,E) }[/math] 中的一个最小割，那么 [math]\displaystyle{ |E|\ge \frac{|V||C|}{2} }[/math]。

Proof.

注意到每个顶点 [math]\displaystyle{ v\in V }[/math] 的度数必然至少为 [math]\displaystyle{ |C| }[/math]，否则所有与 [math]\displaystyle{ v }[/math] 邻接的边即构成了一个割（将点 [math]\displaystyle{ v }[/math] 与其余所有点分开），而且这个割比 [math]\displaystyle{ |C| }[/math] 更小，这就与 [math]\displaystyle{ C }[/math] 是一个最小割相矛盾。

现在由于每个顶点的度至少为 [math]\displaystyle{ |C| }[/math]，应用握手引理，所有顶点度数之和是 [math]\displaystyle{ 2|E|\ge |V||C| }[/math]。（容易验证握手引理对于多重图仍旧成立。）

[math]\displaystyle{ \square }[/math]

令 [math]\displaystyle{ V_i }[/math] 和 [math]\displaystyle{ E_i }[/math] 分别表示多重图 [math]\displaystyle{ G_i }[/math] 的顶点集和边集。注意到 [math]\displaystyle{ |V_{i}|=n-i+1 }[/math]。根据引理2，若 [math]\displaystyle{ C }[/math] 在 [math]\displaystyle{ G_i }[/math] 中仍然是一个最小割，则有 [math]\displaystyle{ |E_i|\ge \frac{(n-i+2)|C|}{2} }[/math]。于是条件概率 [math]\displaystyle{ \Pr[\,e_i\not\in C\mid e_1,e_2,\ldots,e_{i-1}\not\in C\,] }[/math]可被计算如下：

[math]\displaystyle{ \begin{align} \Pr[\,e_i\not\in C\mid e_1,e_2,\ldots,e_{i-1}\not\in C\,] &=1-\frac{|C|}{|E_i|}\\ &\ge 1-\frac{2}{n-i+1}. \end{align} }[/math]

将上述分析归总，可得：

[math]\displaystyle{ \begin{align} \Pr[\,\text{收缩算法输出了 }G\text{ 的一个最小割}\,] &\ge \Pr[\,\text{收缩算法输出了 }C\,]\\ &= \Pr[\,e_1,e_2,\ldots,e_{n-2}\not\in C\,]\\ &= \prod_{i=1}^{n-2}\Pr[\,e_i\not\in C\mid e_1,e_2,\ldots,e_{i-1}\not\in C\,]\\ &\ge \prod_{i=1}^{n-2}\left(1-\frac{2}{n-i+1}\right)\\ &= \prod_{k=3}^{n}\frac{k-2}{k}\\ &= \frac{2}{n(n-1)}. \end{align} }[/math]

这证明了如下定理：

定理（收缩算法的正确概率）

对于 [math]\displaystyle{ n }[/math] 个顶点的任意多重图，收缩算法返回一个最小割的概率至少为 [math]\displaystyle{ \frac{2}{n(n-1)} }[/math]。

初看之下，这一成功概率似乎相当小。然而请注意，一个图中可能存在指数多的割（因为潜在地，每个非空点集 [math]\displaystyle{ S\subset V }[/math] 都可以对应一个将 [math]\displaystyle{ S }[/math] 与其补集分开的割），而Karger算法有效地将这个指数级的解空间事实上缩小到了平方级别。

我们可以独立地运行上述收缩算法 [math]\displaystyle{ t=\left\lceil\frac{n(n-1)\ln n}{2}\right\rceil }[/math] 次，将所有返回的割中最小的一个作为最终结果返回。最终正确得到最小割的概率至少是：

[math]\displaystyle{ \begin{align} &1-\Pr[\,\text{全部 }t\text{ 次独立运行收缩算法都没有找到 }G\text{ 的最小割}\,] \\ = &1-\Pr[\,\text{一次运行收缩算法没有成功输出 }G\text{ 的最小割}\,]^{t} \\ \ge &1- \left(1-\frac{2}{n(n-1)}\right)^{\frac{n(n-1)}{2}\cdot \ln n} \\ \ge &1-\left(\frac{1}{\mathrm{e}}\right)^{\ln n}\\ = &1-\frac{1}{n}. \end{align} }[/math]

一个概率法推论

上述对Karger算法的分析可以导出如下关于图中最小割数量的推论。

推论（最小割数量上界）

对于 [math]\displaystyle{ n }[/math] 个顶点的任意多重图 [math]\displaystyle{ G(V,E) }[/math]，[math]\displaystyle{ G }[/math] 中最小割的数量至多为 [math]\displaystyle{ \frac{n(n-1)}{2} }[/math]。

Proof.

首先定义事件 [math]\displaystyle{ A }[/math] 如下：

[math]\displaystyle{ A: }[/math] “收缩算法输出了图 [math]\displaystyle{ G }[/math] 的某个最小割”。

并对 [math]\displaystyle{ G }[/math] 中每一个不同的最小割 [math]\displaystyle{ C }[/math]，定义事件 [math]\displaystyle{ A_C }[/math] 如下：

[math]\displaystyle{ A_C: }[/math] “收缩算法输出了 [math]\displaystyle{ C }[/math]”。

容易验证，对于图 [math]\displaystyle{ G }[/math] 中的不同最小割 [math]\displaystyle{ C }[/math]，事件 [math]\displaystyle{ A_C }[/math] 彼此不相容；而且，事件 [math]\displaystyle{ A }[/math] 是对所有最小割 [math]\displaystyle{ C }[/math] 事件 [math]\displaystyle{ A_C }[/math] 的并，即

[math]\displaystyle{ A=\bigcup_{G\text{中所有最小割}C}A_C }[/math].

于是根据概率的 [math]\displaystyle{ \sigma }[/math]可加性，有：

[math]\displaystyle{ \Pr(A)=\sum_{G\text{中所有最小割}C}\Pr(A_C) }[/math].

由我们对于Karger算法的分析可得，对任何最小割 [math]\displaystyle{ C }[/math]，都有 [math]\displaystyle{ \Pr(A_c)\ge\frac{2}{n(n-1)} }[/math]。而作为良定义的概率，必然有 [math]\displaystyle{ \Pr(A)\le 1 }[/math]。因此可知，图 [math]\displaystyle{ G }[/math] 中最小割的总数不会超过 [math]\displaystyle{ \frac{n(n-1)}{2} }[/math]。

[math]\displaystyle{ \square }[/math]

上述推论是一个概率法（the probabilistic method）的实例：结论本身不具有任何随机性，但是其证明过程引入了概率论。而且这个结论给出的界是紧的：存在 [math]\displaystyle{ n }[/math] 个顶点的图 [math]\displaystyle{ G }[/math]，其最小割的个数刚好为 [math]\displaystyle{ \frac{n(n-1)}{2} }[/math]，例如：[math]\displaystyle{ n }[/math] 个顶点的环。

@@ Line 9: / Line 9: @@
 等价地，该问题要求找到一个将 <math>V</math> 分成两个不相交非空子集 <math>S</math> 和 <math>T</math> 的划分，使得跨越 <math>S</math> 和 <math>T</math> 的边总数最小。
-我们考虑如下更具一般性的情境：输入图 <math>G</math> 可以是'''多重图'''（'''multigraph'''），这意味着任意两个顶点 <math>u</math> 和 <math>v</math> 之间可能存在多条'''平行边'''（'''parallel edges'''）。多重图中的割的定义与之前相同，割 <math>C</math> 的大小则由 <math>C</math> 中所有边（包括平行边）的总数给出。等价地，可以将多重图视为带有整数边权重的图，割 <math>C</math> 的大小表示为 <math>C</math> 中所有边的总权重。
+我们考虑如下更具一般性的情境：输入图 <math>G</math> 可以是'''多重图'''（'''multigraph'''），这意味着任意两个顶点 <math>u</math> 和 <math>v</math> 之间可能存在多条'''平行边'''（'''parallel edges'''），也称为'''重'''(读音chóng)'''边'''。多重图中的割的定义与之前相同，割 <math>C</math> 的大小则由 <math>C</math> 中所有边（包括平行边）的总数给出。等价地，可以将多重图视为带有整数边权重的图，割 <math>C</math> 的大小表示为 <math>C</math> 中所有边的总权重。
 通过[http://en.wikipedia.org/wiki/Max-flow_min-cut_theorem 最大流-最小割定理]，可以得到这个问题的一个经典的确定性算法。最大流算法可以找到一个最小的'''<math>s</math>-<math>t</math>割''', 将由输入任意指定的一个'''源点''' <math>s\in V</math> 和一个'''汇点''' <math>t\in V</math> 分割开来。然后可以通过穷举来找到针对任意固定源点 <math>s</math> 和所有可能的汇点 <math>t\neq s</math> 的最小 <math>s</math>-<math>t</math> 割，从而求得全局最小割。
@@ Line 15: / Line 15: @@
 == Karger算法 ==
 我们将描述一个简洁优美的随机化算法来解决最小割问题。该算法最初是由[http://people.csail.mit.edu/karger/ David Karger]提出的。
 给定一个多重图 <math>G(V,E)</math> 和一条边 <math>e\in E</math>，我们定义如下的'''收缩'''操作 <math>\mathsf{Contract}(G,e)</math>，将 <math>G</math> 更新为一个新的多重图。
@@ Line 21: / Line 20: @@
 设 <math>e=\{u,v\}</math>：
 :* 将顶点 <math>u,v</math> 替换为一个新顶点 <math>x</math>；
-:* 对于图中任何一条连接 <math>u,v</math> 其中之一到 <math>u,v</math> 以外某顶点 <math>w\in V\setminus{u,v}</math> 的边（无论是否平行），用一条新边 <math>\{x,w\}</math> 替换它；
+:* 对于图中任何一条连接 <math>u,v</math> 其中之一到 <math>u,v</math> 以外某顶点 <math>w\in V\setminus\{u,v\}</math> 的边，用一条新边 <math>\{x,w\}</math> 替换它；
 :* 图中剩余的部分保持不变。
 }}
@@ Line 36: / Line 35: @@
 ----
 :while <math>|V|>2</math> do
-:* 从当前图中依均匀分布选择一条随机的边 <math>e\in E</math>;
+:* 从当前图中均匀分布地选择一条随机的边 <math>e\in E</math>;
 :* <math>G=\mathsf{Contract}(G,e)</math>;
 :return <math>C=E</math> (即当前所剩的最后两个顶点之间所有的平行边);
@@ Line 42: / Line 41: @@
 另一种看待收缩操作 <math>\mathsf{Contract}(G,e)</math> 的方式是将其解读为对两个顶点的等价类的合并。假设 <math>V={v_1,v_2,\ldots,v_n}</math> 是所有顶点的集合。我们从 <math>n</math> 个顶点等价类 <math>S_1,S_2,\ldots, S_n</math> 开始，其中每个等价类 <math>S_i={v_i}</math> 包含一个顶点。通过调用 <math>\mathsf{Contract}(G,e)</math>，其中 <math>e</math> 跨越了两个不同的等价类 <math>S_i</math> 和 <math>S_j</math>，其效果是将等价类 <math>S_i</math> 和 <math>S_j</math> 合并。收缩后的多重图中的边就是跨越不同顶点等价类之间的边。
-这一视角如图所示：
+这一视角的效果如图所示：
 [[Image:Contract_class.png|600px|center]]
-== Analysis of Karger's Algorithm ==
+== Karger算法的分析 ==
-We now analyze the above algorithm. Since the algorithm is '''''randomized''''', its output cut is random even when the input is fixed, so ''the output may not always be correct''. We want to give a theoretical guarantee of the chance that the algorithm returns a correct answer on an arbitrary input.
+假设输入图 <math>G</math> 为一任意给定的多重图。Karger算法输出了该图的一个随机的割。我们需要分析该随机割是最小割的概率，即如下概率的下界：
+:<math>\Pr[\,\text{收缩算法输出了 }G\text{ 的一个最小割}\,]</math>.
-More precisely, on an arbitrarily fixed input multi-graph <math>G</math>, we want to answer the following question rigorously:
-:<math>p_{\text{correct}}=\Pr[\,\text{a minimum cut is returned by }RandomContract\,]\ge ?</math>
-To answer this question, we prove a stronger statement: for arbitrarily fixed input multi-graph <math>G</math> and a particular minimum cut <math>C</math> in <math>G</math>,
+对此，我们证明如下更强的结论。令 <math>C</math> 是输入图 <math>G</math> 中的某个特定的最小割。我们将分析如下概率的下界：
-:<math>p_{C}=\Pr[\,C\mbox{ is returned by }RandomContract\,]\ge ?</math>
+:<math>\Pr[\,\text{收缩算法输出了 }C\,]</math>.
-Obviously this will imply the previous lower bound for <math>p_{\text{correct}}</math> because the event in <math>p_{C}</math> implies the event in <math>p_{\text{correct}}</math>.
+显然这一概率是收缩算法成功输出最小割的概率的下界（在这里我们使用了如下概率法则：对任意事件 <math>A</math> 和 <math>B</math>，若 <math>A\subseteq B</math>，则<math>\Pr(A)\le \Pr(B)</math>）。
-:{|border="2" width="100%" cellspacing="4" cellpadding="3" rules="all" style="margin:1em 1em 1em 0; border:solid 1px #AAAAAA; border-collapse:collapse;empty-cells:show;"
-|
-*In above argument we use the simple law in probability that <math>\Pr(A)\le \Pr(B)</math> if <math>A\subseteq B</math>, i.e. event <math>A</math> implies event <math>B</math>.
-|}
-We introduce the following notations:
+我们引入以下记号：
-*Let <math>e_1,e_2,\ldots,e_{n-2}</math> denote the sequence of random edges chosen to contract in a running of ''RandomContract'' algorithm.
+* 令 <math>e_1,e_2,\ldots,e_{n-2}</math> 表示在运行收缩算法时，依次选中进行收缩的随机边的序列；
-*Let <math>G_1=G</math> denote the original input multi-graph. And for <math>i=1,2,\ldots,n-2</math>, let <math>G_{i+1}=Contract(G_{i},e_i)</math> be the multigraph after <math>i</math>th contraction.
+* 令 <math>G_1=G</math> 表示最初输入的多重图。对于 <math>i=1,2,\ldots,n-2</math>，令 <math>G_{i+1}=\mathsf{Contract}(G_{i},e_i)</math> 表示第 <math>i</math> 轮收缩后的多重图。
-Obviously <math>e_1,e_2,\ldots,e_{n-2}</math> are random, and they are the ''only'' random choices used in the algorithm: meaning that they along with the input <math>G</math>, uniquely determine the sequence of multi-graphs <math>G_1,G_2,\ldots,G_{n-2}</math> in every iteration as well as the final output.
-We now compute the probability <math>p_C</math> by decompose it into more elementary events involving <math>e_1,e_2,\ldots,e_{n-2}</math>. This is due to the following proposition.
+我们可以做出如下的观察：
 {{Theorem
-|Proposition 1|
+|引理 1|
-:If <math>C</math> is a minimum cut in a multi-graph <math>G</math> and <math>e\not\in C</math>, then <math>C</math> is still a minimum cut in the contracted graph <math>G'=contract(G,e)</math>.
+:如果 <math>C</math> 是多重图 <math>G</math> 中的一个最小割，且 <math>e\not\in C</math>，那么 <math>C</math> 在收缩图 <math>G'=\mathsf{Contract}(G,e)</math> 中仍然是一个最小割。}}
-}}
 {{Proof|
-We first observe that contraction will never create new cuts: every cut in the contracted graph <math>G'</math> must also be a cut in the original graph <math>G</math>.
+我们首先观察到，收缩永远不会创建新的割：收缩图 <math>G'</math> 中的每个割也必定是原图 <math>G</math> 中的一个割。
-We then observe that a cut <math>C</math> in <math>G</math> "survives" in the contracted graph <math>G'</math> if and only if the contracted edge <math>e\not\in C</math>.
+然后我们观察到，原始图 <math>G</math> 中的割 <math>C</math> 能在收缩图 <math>G'</math> 中幸存，当且仅当收缩边 <math>e\not\in C</math>。
-Both observations are easy to verify by the definition of contraction operator (in particular, easier to verify if we take the vertex class interpretation).
+这两个观察都很容易通过收缩操作的定义进行验证（特别是在考虑顶点等价类的解释时更容易验证）。
 }}
-Recall that <math>e_1,e_2,\ldots,e_{n-2}</math> denote the sequence of random edges chosen to contract in a running of ''RandomContract'' algorithm.
+根据'''引理1'''，我们有：
+:<math>\Pr[\,\text{收缩算法输出了 }C\,]=\Pr[\,e_1,e_2,\ldots,e_{n-2}\not\in C\,]</math>;
+再根据链式法则，这一概率可被计算如下：
+:<math>\Pr[\,e_1,e_2,\ldots,e_{n-2}\not\in C\,]=\prod_{i=1}^{n-2}\Pr[\,e_i\not\in C\mid e_1,e_2,\ldots,e_{i-1}\not\in C\,]</math>.
-By Proposition 1, the event <math>\mbox{``}C\mbox{ is returned by }RandomContract\mbox{''}\,</math> is equivalent to the event <math>\mbox{``}e_i\not\in C\mbox{ for all }i=1,2,\ldots,n-2\mbox{''}</math>. Therefore:
+接下来我们的任务是对每个条件概率 <math>\Pr[\,e_i\not\in C\mid e_1,e_2,\ldots,e_{i-1}\not\in C\,]</math> 给出下界。注意到：根据'''引理1'''，条件 <math>e_1,e_2,\ldots,e_{i-1}\not\in C</math> 的发生意味着 <math>C</math> 仍是当前图 <math>G_i</math> 中的最小割；而 <math>e_i</math> 是图 <math>G_i</math> 中的一条均匀分布的随机边。于是条件概率 <math>\Pr[\,e_i\not\in C\mid e_1,e_2,\ldots,e_{i-1}\not\in C\,]</math> 即为图 <math>G_i</math> 中一条均匀随机边未命中其某个最小割 <math>C</math> 的概率。直观上：“最小”割应该在边集中相对稀疏，因此这一概率应该有下界。如下引理严格印证了这一直觉。
-:<math>
-\begin{align}
-p_C
-&=
-\Pr[\,C\mbox{ is returned by }{RandomContract}\,]\\
-&=
-\Pr[\,e_i\not\in C\mbox{ for all }i=1,2,\ldots,n-2\,]\\
-&=
-\prod_{i=1}^{n-2}\Pr[e_i\not\in C\mid \forall j<i, e_j\not\in C].
-\end{align}
-</math>
-The last equation is due to the '''chain rule'''.
-Now our task is to give lower bound to each <math>p_i=\Pr[e_i\not\in C\mid \forall j<i, e_j\not\in C]</math>. The condition <math>\mbox{``}\forall j<i, e_j\not\in C\mbox{''}</math> means the min-cut <math>C</math> survives all first <math>i-1</math> contractions <math>e_1,e_2,\ldots,e_{i-1}</math>, which due to Proposition 1 means that <math>C</math> is also a min-cut in the multi-graph <math>G_i</math> obtained from applying the first <math>(i-1)</math> contractions.
-Then the conditional probability <math>p_i=\Pr[e_i\not\in C\mid \forall j<i, e_j\not\in C]</math> is the probability that no edge in <math>C</math> is hit when a uniform random edge in the current multi-graph is chosen assuming that <math>C</math> is a minimum cut in the current multi-graph. Intuitively this probability should be bounded from below, because as a min-cut <math>C</math> should be sparse among all edges. This intuition is justified by the following proposition.
 {{Theorem
-|Proposition 2|
+|引理 2|
-:If <math>C</math> is a min-cut in a multi-graph <math>G(V,E)</math>, then <math>|E|\ge \frac{|V||C|}{2}</math>.
+:如果 <math>C</math> 是多重图 <math>G(V,E)</math> 中的一个最小割，那么 <math>|E|\ge \frac{|V||C|}{2}</math>。
 }}
 {{Proof|
-:It must hold that the degree of each vertex <math>v\in V</math> is at least <math>|C|</math>, or otherwise the set of edges incident to <math>v</math> forms a cut of size smaller than <math>|C|</math> which separates <math>\{v\}</math> from the rest of the graph, contradicting that <math>C</math> is a min-cut. And the bound <math>|E|\ge \frac{|V||C|}{2}</math> follows directly from applying the [https://en.wikipedia.org/wiki/Handshaking_lemma handshaking lemma] to the fact that every vertex in <math>G</math> has degree at least <math>|C|</math>.
+:注意到每个顶点 <math>v\in V</math> 的度数必然至少为 <math>|C|</math>，否则所有与 <math>v</math> 邻接的边即构成了一个割（将点 <math>v</math> 与其余所有点分开），而且这个割比  <math>|C|</math> 更小，这就与 <math>C</math> 是一个最小割相矛盾。
+:现在由于每个顶点的度至少为 <math>|C|</math>，应用[https://en.wikipedia.org/wiki/Handshaking_lemma 握手引理]，所有顶点度数之和是 <math>2|E|\ge |V||C|</math>。（容易验证握手引理对于多重图仍旧成立。）
 }}
-Let <math>V_i</math> and <math>E_i</math> denote the vertex set and edge set of the multi-graph <math>G_i</math> respectively, and recall that <math>G_i</math> is the multi-graph obtained from applying first <math>(i-1)</math> contractions. Obviously <math>|V_{i}|=n-i+1</math>. And due to Proposition 2, <math>|E_i|\ge \frac{|V_i||C|}{2}</math> if <math>C</math> is still a min-cut in <math>G_i</math>.
+令 <math>V_i</math> 和 <math>E_i</math> 分别表示多重图 <math>G_i</math> 的顶点集和边集。注意到 <math>|V_{i}|=n-i+1</math>。根据'''引理2'''，若 <math>C</math> 在 <math>G_i</math> 中仍然是一个最小割，则有 <math>|E_i|\ge \frac{(n-i+2)|C|}{2}</math>。于是条件概率 <math>\Pr[\,e_i\not\in C\mid e_1,e_2,\ldots,e_{i-1}\not\in C\,]</math>可被计算如下：
-The probability <math>p_i=\Pr[e_i\not\in C\mid \forall j<i, e_j\not\in C]</math> can be computed as
 :<math>
 \begin{align}
-p_i
+\Pr[\,e_i\not\in C\mid e_1,e_2,\ldots,e_{i-1}\not\in C\,]
 &=1-\frac{|C|}{|E_i|}\\
-&\ge1-\frac{2}{|V_i|}\\
+&\ge 1-\frac{2}{n-i+1}.
-&=1-\frac{2}{n-i+1}
+\end{align}</math>
-\end{align},</math>
-where the inequality is due to Proposition 2.
-We now can put everything together. We arbitrarily fix the input multi-graph <math>G</math> and any particular minimum cut <math>C</math> in <math>G</math>.
+将上述分析归总，可得：
 :<math>\begin{align}
-p_{\text{correct}}
+\Pr[\,\text{收缩算法输出了 }G\text{ 的一个最小割}\,]
-&=\Pr[\,\text{a minimum cut is returned by }RandomContract\,]\\
 &\ge
-\Pr[\,C\mbox{ is returned by }{RandomContract}\,]\\
+\Pr[\,\text{收缩算法输出了 }C\,]\\
 &=
-\Pr[\,e_i\not\in C\mbox{ for all }i=1,2,\ldots,n-2\,]\\
+\Pr[\,e_1,e_2,\ldots,e_{n-2}\not\in C\,]\\
 &=
-\prod_{i=1}^{n-2}\Pr[e_i\not\in C\mid \forall j<i, e_j\not\in C]\\
+\prod_{i=1}^{n-2}\Pr[\,e_i\not\in C\mid e_1,e_2,\ldots,e_{i-1}\not\in C\,]\\
 &\ge
 \prod_{i=1}^{n-2}\left(1-\frac{2}{n-i+1}\right)\\
@@ Line 134: / Line 108: @@
 \end{align}</math>
-This gives us the following theorem.
+这证明了如下定理：
 {{Theorem
-|Theorem|
+|定理（收缩算法的正确概率）|
-: For any multigraph with <math>n</math> vertices, the ''RandomContract'' algorithm returns a minimum cut with probability at least <math>\frac{2}{n(n-1)}</math>.
+:对于 <math>n</math> 个顶点的任意多重图，收缩算法返回一个最小割的概率至少为 <math>\frac{2}{n(n-1)}</math>。
 }}
-At first glance this seems to be a quite slim chance of success. However, notice that there may be exponential many cuts in a graph (because potentially every nonempty subset <math>S\subset V</math> corresponds to a cut <math>C=E(S,\overline{S})</math>), and Karger's algorithm effectively reduce this exponential-sized space to quadratic-sized, an exponential improvement!
+初看之下，这一成功概率似乎相当小。然而请注意，一个图中可能存在指数多的割（因为潜在地，每个非空点集 <math>S\subset V</math> 都可以对应一个将 <math>S</math> 与其补集分开的割），而Karger算法有效地将这个指数级的解空间事实上缩小到了平方级别。
-We can run ''RandomContract'' independently for <math>t=\left\lceil\frac{n(n-1)\ln n}{2}\right\rceil</math> times and return the smallest cut ever returned. The probability that a minimum cut is found is at least:
+我们可以独立地运行上述收缩算法 <math>t=\left\lceil\frac{n(n-1)\ln n}{2}\right\rceil</math> 次，将所有返回的割中最小的一个作为最终结果返回。最终正确得到最小割的概率至少是：
 :<math>\begin{align}
-&\quad 1-\Pr[\,\mbox{all }t\mbox{ independent runnings of } RandomContract\mbox{ fails to find a min-cut}\,] \\
+&1-\Pr[\,\text{全部 }t\text{ 次独立运行收缩算法都没有找到 }G\text{ 的最小割}\,] \\
-&= 1-\Pr[\,\mbox{a single running of }{RandomContract}\mbox{ fails}\,]^{t} \\
+=
-&\ge 1- \left(1-\frac{2}{n(n-1)}\right)^{\frac{n(n-1)\ln n}{2}} \\
+&1-\Pr[\,\text{一次运行收缩算法没有成功输出 }G\text{ 的最小割}\,]^{t} \\
-&\ge 1-\frac{1}{n}.
+\ge
+&1- \left(1-\frac{2}{n(n-1)}\right)^{\frac{n(n-1)}{2}\cdot \ln n} \\
+\ge
+&1-\left(\frac{1}{\mathrm{e}}\right)^{\ln n}\\
+=
+&1-\frac{1}{n}.
 \end{align}</math>
-== A Consequence of the Probabilistic Method ==
+== 一个概率法推论 ==
-The analysis of Karger's algorithm implies the following combinatorial proposition for the number of distinct minimum cuts in a graph.
+上述对Karger算法的分析可以导出如下关于图中最小割数量的推论。
-{{Theorem|Corollary|
+{{Theorem|推论（最小割数量上界）|
-:For any graph <math>G(V,E)</math> of <math>n</math> vertices, the number of distinct minimum cuts in <math>G</math> is at most <math>\frac{n(n-1)}{2}</math>.
+:对于 <math>n</math> 个顶点的任意多重图 <math>G(V,E)</math>，<math>G</math> 中最小割的数量至多为 <math>\frac{n(n-1)}{2}</math>。
 }}
 {{Proof|
-Let <math>\mathcal{C}</math> denote the set of all minimum cuts in <math>G</math>. For each min-cut <math>C\in\mathcal{C}</math>, let <math>A_C</math> denote the event "<math>C</math> is returned by ''RandomContract''", whose probability is given by
+首先定义事件 <math>A</math> 如下：
-:<math>p_C=\Pr(A_C)\,</math>.
+:<math>A:</math> “收缩算法输出了图 <math>G</math> 的某个最小割”。
+并对 <math>G</math> 中每一个不同的最小割 <math>C</math>，定义事件 <math>A_C</math> 如下：
-Clearly we have:
+:<math>A_C:</math> “收缩算法输出了 <math>C</math>”。
-* for any distinct <math>C,D\in\mathcal{C}</math>, <math>A_C\,</math> and <math>A_{D}\,</math> are '''disjoint events'''; and
+容易验证，对于图 <math>G</math> 中的不同最小割 <math>C</math>，事件 <math>A_C</math> 彼此不相容；而且，事件 <math>A</math> 是对所有最小割 <math>C</math> 事件 <math>A_C</math> 的并，即
-* the union <math>\bigcup_{C\in\mathcal{C}}A_C</math> is precisely the event "a minimum cut is returned by ''RandomContract''", whose probability is given by
+:<math>A=\bigcup_{G\text{中所有最小割}C}A_C</math>.
-::<math>p_{\text{correct}}=\Pr[\,\text{a minimum cut is returned by } RandomContract\,]</math>.
+于是根据概率的 <math>\sigma</math>可加性，有：
-Due to the [https://en.wikipedia.org/wiki/Probability_axioms#Third_axiom '''additivity of probability'''], it holds that
+:<math>\Pr(A)=\sum_{G\text{中所有最小割}C}\Pr(A_C)</math>.
-:<math>
-p_{\text{correct}}=\sum_{C\in\mathcal{C}}\Pr(A_C)=\sum_{C\in\mathcal{C}}p_C.
-</math>
-By the analysis of Karger's algorithm, we know <math>p_C\ge\frac{2}{n(n-1)}</math>. And since <math>p_{\text{correct}}</math> is a well defined probability, due to the [https://en.wikipedia.org/wiki/Probability_axioms#Second_axiom '''unitarity of probability'''], it must hold that <math>p_{\text{correct}}\le 1</math>. Therefore,
+由我们对于Karger算法的分析可得，对任何最小割 <math>C</math>，都有 <math>\Pr(A_c)\ge\frac{2}{n(n-1)}</math>。而作为良定义的概率，必然有 <math>\Pr(A)\le 1</math>。因此可知，图 <math>G</math> 中最小割的总数不会超过 <math>\frac{n(n-1)}{2}</math>。
-:<math>1\ge p_{\text{correct}}=\sum_{C\in\mathcal{C}}p_C\ge|\mathcal{C}|\frac{2}{n(n-1)}</math>,
-which means <math>|\mathcal{C}|\le\frac{n(n-1)}{2}</math>.
 }}
-Note that the statement of this theorem has no randomness at all, while the proof consists of a randomized procedure. This is an example of [http://en.wikipedia.org/wiki/Probabilistic_method the probabilistic method].
+上述推论是一个'''概率法'''（'''the probabilistic method'''）的实例：结论本身不具有任何随机性，但是其证明过程引入了概率论。而且这个结论给出的界是紧的：存在 <math>n</math> 个顶点的图 <math>G</math>，其最小割的个数刚好为  <math>\frac{n(n-1)}{2}</math>，例如：<math>n</math> 个顶点的环。

概率论与数理统计 (Spring 2024)/Karger's min-cut algorithm: Difference between revisions

Latest revision as of 14:44, 19 March 2024

Karger算法

Karger算法的分析

一个概率法推论

Navigation menu

Search