Combinatorics (Fall 2010)/Partitions, sieve methods: Difference between revisions
imported>WikiSysop |
imported>WikiSysop No edit summary |
||
| Line 1: | Line 1: | ||
== Principle of Inclusion-Exclusion == | == Principle of Inclusion-Exclusion == | ||
Let <math>A_1,A_2,\ldots,A_n</math> be a | Let <math>A</math> and <math>B</math> be two finite sets. The cardinality of their union is | ||
:<math>|A\cup B|=|A|+|B|-{\color{Blue}|A\cap B|}</math>. | |||
For three sets <math>A</math>, <math>B</math>, and <math>C</math>, the cardinality of the union of these three sets is computed as | |||
:<math>|A\cup B\cup C|=|A|+|B|+|C|-{\color{Blue}|A\cap B|}-{\color{Blue}|A\cap C|}-{\color{Blue}|B\cap C|}+{\color{Red}|A\cap B\cap C|}</math>. | |||
This is illustrated by the following figure. | |||
[[Image:Inclusion-exclusion.png|center]] | |||
Generally, the '''Principle of Inclusion-Exclusion''' states the rule for computing the union of <math>n</math> finite sets <math>A_1,A_2,\ldots,A_n</math>, such that | |||
{{Equation| | |||
<math> | |||
\begin{align} | |||
\left|\bigcup_{i=1}^nA_i\right| | |||
&= | |||
\sum_{I\subseteq\{1,\ldots,n\}}(-1)^{|I|-1}\left|\bigcap_{i\in I}A_i\right|. | |||
\end{align} | |||
</math> | |||
}} | |||
----- | |||
In combinatorics, we usually apply the complement form of the Principle of Inclusion-Exclusion. | |||
Let <math>A_1,A_2,\ldots,A_n\subseteq U</math> be subsets of some finite set <math>U</math>. Here <math>U</math> is some universe of combinatorial objects, whose cardinality is easy to calculate (e.g. all strings, tuples, permutations), and each <math>A_i</math> contains the objects with some specific property (e.g. a "pattern") which we want to avoid. The problem is to count the number of objects without any of the <math>n</math> properties. We write <math>\bar{A_i}=U-A</math>. The number of objects without any of the properties <math>A_1,A_2,\ldots,A_n</math> is | |||
{{Equation| | |||
<math> | |||
\begin{align} | |||
\left|\bar{A_1}\cap\bar{A_2}\cap\cdots\cap\bar{A_n}\right|=\left|U-\bigcup_{i=1}^nA_i\right| | |||
&= | |||
|U|-\sum_{I\subseteq\{1,\ldots,n\}}(-1)^{|I|}\left|\bigcap_{i\in I}A_i\right|. | |||
\end{align} | |||
</math> | |||
}} | |||
For an <math>I\subseteq\{1,2,\ldots,n\}</math>, we denote | For an <math>I\subseteq\{1,2,\ldots,n\}</math>, we denote | ||
:<math>A_I=\bigcap_{i\in I}A_i</math> | :<math>A_I=\bigcap_{i\in I}A_i</math> | ||
with the convention that <math>A_\emptyset=U</math>. | with the convention that <math>A_\emptyset=U</math>. The above equation is stated as: | ||
{{Theorem|Principle of Inclusion-Exclusion| | {{Theorem|Principle of Inclusion-Exclusion| | ||
:Let <math>A_1,A_2,\ldots,A_n</math> be a family of subsets of <math>U</math>. Then the number of elements of <math>U</math> which lie in none of the subsets <math>A_i</math> is | :Let <math>A_1,A_2,\ldots,A_n</math> be a family of subsets of <math>U</math>. Then the number of elements of <math>U</math> which lie in none of the subsets <math>A_i</math> is | ||
| Line 9: | Line 39: | ||
}} | }} | ||
Let <math>S_k=\sum_{|I|=k}|A_I|\,</math>. Conventionally, <math>S_0=|A_\emptyset|</math>. The principle of inclusion-exclusion can be | Let <math>S_k=\sum_{|I|=k}|A_I|\,</math>. Conventionally, <math>S_0=|A_\emptyset|=|U|</math>. The principle of inclusion-exclusion can be expressed as | ||
{{Equation|<math> | |||
S_0-S_1+S_2+\cdots+(-1)^nS_n. | S_0-S_1+S_2+\cdots+(-1)^nS_n. | ||
</math> | </math> | ||
}} | |||
=== Surjections === | |||
== Permutations == | == Permutations == | ||
Revision as of 06:03, 15 July 2010
Principle of Inclusion-Exclusion
Let [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] be two finite sets. The cardinality of their union is
- [math]\displaystyle{ |A\cup B|=|A|+|B|-{\color{Blue}|A\cap B|} }[/math].
For three sets [math]\displaystyle{ A }[/math], [math]\displaystyle{ B }[/math], and [math]\displaystyle{ C }[/math], the cardinality of the union of these three sets is computed as
- [math]\displaystyle{ |A\cup B\cup C|=|A|+|B|+|C|-{\color{Blue}|A\cap B|}-{\color{Blue}|A\cap C|}-{\color{Blue}|B\cap C|}+{\color{Red}|A\cap B\cap C|} }[/math].
This is illustrated by the following figure.
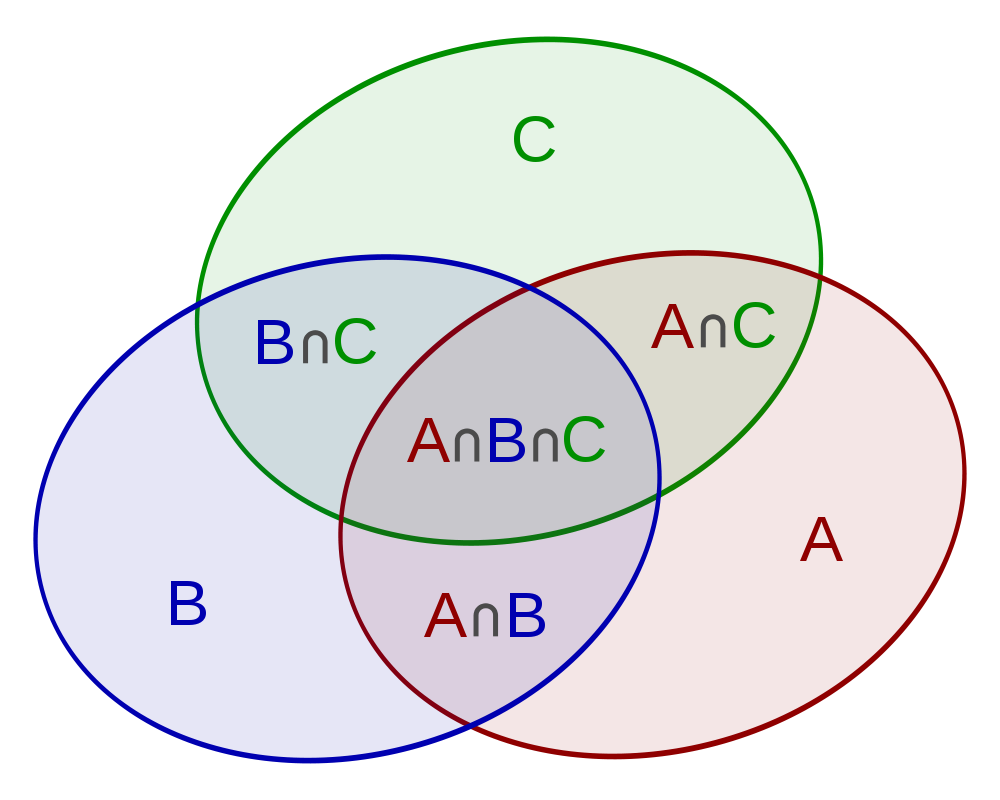
Generally, the Principle of Inclusion-Exclusion states the rule for computing the union of [math]\displaystyle{ n }[/math] finite sets [math]\displaystyle{ A_1,A_2,\ldots,A_n }[/math], such that
[math]\displaystyle{ \begin{align} \left|\bigcup_{i=1}^nA_i\right| &= \sum_{I\subseteq\{1,\ldots,n\}}(-1)^{|I|-1}\left|\bigcap_{i\in I}A_i\right|. \end{align} }[/math]
In combinatorics, we usually apply the complement form of the Principle of Inclusion-Exclusion.
Let [math]\displaystyle{ A_1,A_2,\ldots,A_n\subseteq U }[/math] be subsets of some finite set [math]\displaystyle{ U }[/math]. Here [math]\displaystyle{ U }[/math] is some universe of combinatorial objects, whose cardinality is easy to calculate (e.g. all strings, tuples, permutations), and each [math]\displaystyle{ A_i }[/math] contains the objects with some specific property (e.g. a "pattern") which we want to avoid. The problem is to count the number of objects without any of the [math]\displaystyle{ n }[/math] properties. We write [math]\displaystyle{ \bar{A_i}=U-A }[/math]. The number of objects without any of the properties [math]\displaystyle{ A_1,A_2,\ldots,A_n }[/math] is
[math]\displaystyle{ \begin{align} \left|\bar{A_1}\cap\bar{A_2}\cap\cdots\cap\bar{A_n}\right|=\left|U-\bigcup_{i=1}^nA_i\right| &= |U|-\sum_{I\subseteq\{1,\ldots,n\}}(-1)^{|I|}\left|\bigcap_{i\in I}A_i\right|. \end{align} }[/math]
For an [math]\displaystyle{ I\subseteq\{1,2,\ldots,n\} }[/math], we denote
- [math]\displaystyle{ A_I=\bigcap_{i\in I}A_i }[/math]
with the convention that [math]\displaystyle{ A_\emptyset=U }[/math]. The above equation is stated as:
Principle of Inclusion-Exclusion - Let [math]\displaystyle{ A_1,A_2,\ldots,A_n }[/math] be a family of subsets of [math]\displaystyle{ U }[/math]. Then the number of elements of [math]\displaystyle{ U }[/math] which lie in none of the subsets [math]\displaystyle{ A_i }[/math] is
- [math]\displaystyle{ \sum_{I\subseteq\{1,\ldots, n\}}(-1)^{|I|}|A_I| }[/math].
- Let [math]\displaystyle{ A_1,A_2,\ldots,A_n }[/math] be a family of subsets of [math]\displaystyle{ U }[/math]. Then the number of elements of [math]\displaystyle{ U }[/math] which lie in none of the subsets [math]\displaystyle{ A_i }[/math] is
Let [math]\displaystyle{ S_k=\sum_{|I|=k}|A_I|\, }[/math]. Conventionally, [math]\displaystyle{ S_0=|A_\emptyset|=|U| }[/math]. The principle of inclusion-exclusion can be expressed as