高级算法 (Fall 2016)/Min-Cut and Max-Cut

under construction

Graph Cut

Let [math]\displaystyle{ G(V, E) }[/math] be an undirected graph. A subset [math]\displaystyle{ C\subseteq E }[/math] of edges is a cut of graph [math]\displaystyle{ G }[/math] if [math]\displaystyle{ G }[/math] becomes disconnected after deleting all edges in [math]\displaystyle{ C }[/math].

More formally, a pair of disjoint subsets [math]\displaystyle{ S,T\subseteq V }[/math] of vertices is called a bipartition of [math]\displaystyle{ V }[/math] if [math]\displaystyle{ S }[/math] and [math]\displaystyle{ T }[/math] are not empty and [math]\displaystyle{ S\cup T=V }[/math]. Given a bipartition [math]\displaystyle{ \{S,T\} }[/math] of [math]\displaystyle{ V }[/math], we denote by

[math]\displaystyle{ E(S,T)=\{uv\in E\mid u\in S, v\in T\} }[/math]

the set of "crossing edges" with one endpoint in each of [math]\displaystyle{ S }[/math] and [math]\displaystyle{ T }[/math].

Then every cut [math]\displaystyle{ C\subseteq E }[/math] in [math]\displaystyle{ G }[/math] corresponds to a

[math]\displaystyle{ C=E(S,T),\quad \{S,T\}\mbox{ is a bipartition of }V }[/math].

Given a graph [math]\displaystyle{ G }[/math], there might be many cuts in [math]\displaystyle{ G }[/math], and we are interested in finding its minimum or maximum cut.

Min-Cut

The min-cut problem, also called the global minimum cut problem, is defined as follows.

Min-cut problem

Input: an undirected graph [math]\displaystyle{ G(V,E) }[/math]; Output: a cut [math]\displaystyle{ C }[/math] in [math]\displaystyle{ G }[/math] with the smallest size [math]\displaystyle{ |C| }[/math].

Equivalently, the problem asks to find a bipartition of [math]\displaystyle{ V }[/math] into disjoint non-empty subsets [math]\displaystyle{ S }[/math] and [math]\displaystyle{ T }[/math] that minimizes [math]\displaystyle{ |E(S,T)| }[/math].

We consider the problem in a slightly more generalized setting, where the input graphs [math]\displaystyle{ G }[/math] can be multi-graphs, meaning that there could be multiple edges between two vertices [math]\displaystyle{ u }[/math] and [math]\displaystyle{ v }[/math]. We call such edges the parallel edges. The cuts in multi-graphs are defined in the same way as before, and the cost of a cut [math]\displaystyle{ C }[/math] is given by the total number of edges (including parallel edges) in [math]\displaystyle{ C }[/math]. Equivalently, one may think of a multi-graph as a graph with integer edge weights, and the cost of a cut [math]\displaystyle{ C }[/math] is the total weights of all edges in [math]\displaystyle{ C }[/math].

A canonical deterministic algorithm for this problem is through the max-flow min-cut theorem. The max-flow algorithm finds us a minimum [math]\displaystyle{ s }[/math]-[math]\displaystyle{ t }[/math] cut, which disconnects a source [math]\displaystyle{ s\in V }[/math] from a sink [math]\displaystyle{ t\in V }[/math], both specified as part of the input. A global min cut can be found by exhaustively finding the minimum [math]\displaystyle{ s }[/math]-[math]\displaystyle{ t }[/math] cut for an arbitrarily fixed source [math]\displaystyle{ s }[/math] and all possible sink [math]\displaystyle{ t\neq s }[/math]. This takes [math]\displaystyle{ (n-1)\times }[/math]max-flow time where [math]\displaystyle{ n=|V| }[/math] is the number of vertices.

The fastest known deterministic algorithm for the minimum cut problem on multi-graphs is the Stoer–Wagner algorithm, which achieves an [math]\displaystyle{ O(mn+n^2\log n) }[/math] time complexity where [math]\displaystyle{ m=|E| }[/math] is the total number of edges (counting the parallel edges).

If we restrict the input to be simple graphs (meaning there is no parallel edges) with no edge weight, there are better algorithms. The most recent one was published in STOC 2015, achieving a near-linear (in the number of edges) time complexity.

Karger's Contraction algorithm

We will describe a simple and elegant randomized algorithm for the min-cut problem. The algorithm is due to David Karger.

Let [math]\displaystyle{ G(V, E) }[/math] be a multi-graph, which allows more than one parallel edges between two distinct vertices [math]\displaystyle{ u }[/math] and [math]\displaystyle{ v }[/math] but does not allow any self-loops: the edges that adjoin a vertex to itself. A multi-graph [math]\displaystyle{ G }[/math] can be represented by an adjacency matrix [math]\displaystyle{ A }[/math], in the way that each non-diagonal entry [math]\displaystyle{ A(u,v) }[/math] takes nonnegative integer values instead of just 0 or 1, representing the number of parallel edges between [math]\displaystyle{ u }[/math] and [math]\displaystyle{ v }[/math] in [math]\displaystyle{ G }[/math], and all diagonal entries [math]\displaystyle{ A(v,v)=0 }[/math] (since there is no self-loop).

Given a multi-graph [math]\displaystyle{ G(V,E) }[/math] and an edge [math]\displaystyle{ e\in E }[/math], we define the following contraction operator Contract([math]\displaystyle{ G }[/math], [math]\displaystyle{ e }[/math]), which transform [math]\displaystyle{ G }[/math] to a new multi-graph.

The contraction operator Contract([math]\displaystyle{ G }[/math], [math]\displaystyle{ e }[/math])

say [math]\displaystyle{ e=uv }[/math]: replace [math]\displaystyle{ \{u,v\} }[/math] by a new vertex [math]\displaystyle{ x }[/math]; for every edge (no matter parallel or not) in the form of [math]\displaystyle{ uw }[/math] or [math]\displaystyle{ vw }[/math] that connects one of [math]\displaystyle{ \{u,v\} }[/math] to a vertex [math]\displaystyle{ w\in V\setminus\{u,v\} }[/math] in the graph other than [math]\displaystyle{ u,v }[/math], replace it by a new edge [math]\displaystyle{ xw }[/math]; the reset of the graph does not change.

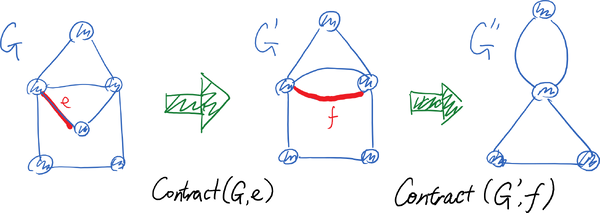
In other words, the [math]\displaystyle{ Contract(G,uv) }[/math] merges the two vertices [math]\displaystyle{ u }[/math] and [math]\displaystyle{ v }[/math] into a new vertex [math]\displaystyle{ x }[/math] whose incident edges preserves the edges incident to [math]\displaystyle{ u }[/math] or [math]\displaystyle{ v }[/math] in the original graph [math]\displaystyle{ G }[/math] except for the parallel edges between them. Now you should realize why we consider multi-graphs instead of simple graphs, because even if we start with a simple graph without parallel edges, the contraction operator may create parallel edges.

The contraction operator is illustrated by the following picture:

Karger's algorithm uses a simple idea:

• At each step we randomly select an edge in the current multi-graph to contract until there are only two vertices left.
• The parallel edges between these two remaining vertices must be a cut of the original graph.
• We return this cut and hope that with good chance this gives us a minimum cut.

The following is the pseudocode for Karger's algorithm.

RandomContract (Karger 1993)

Input: multi-graph [math]\displaystyle{ G(V,E) }[/math]; while [math]\displaystyle{ |V|\gt 2 }[/math] do choose an edge [math]\displaystyle{ uv\in E }[/math] uniformly at random; [math]\displaystyle{ G=Contract(G,uv) }[/math]; return [math]\displaystyle{ C=E }[/math] (the parallel edges between the only two vertices in [math]\displaystyle{ V }[/math]);

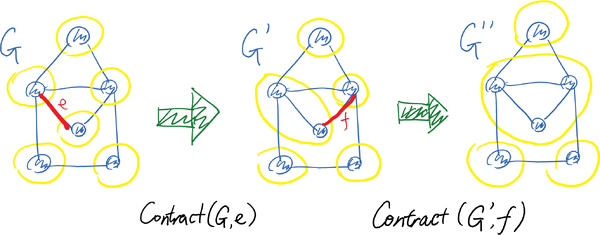
Another way of looking at the contraction operator Contract([math]\displaystyle{ G }[/math],[math]\displaystyle{ e }[/math]) is that we are dealing with classes of vertices. Let [math]\displaystyle{ V=\{v_1,v_2,\ldots,v_n\} }[/math] be the set of all vertices. We start with [math]\displaystyle{ n }[/math] vertex classes [math]\displaystyle{ S_1,S_2,\ldots, S_n }[/math] with each class [math]\displaystyle{ S_i=\{v_i\} }[/math] contains one vertex. By calling [math]\displaystyle{ Contract(G,uv) }[/math], where [math]\displaystyle{ u\in S_i }[/math] and [math]\displaystyle{ v\in S_j }[/math] for distinct [math]\displaystyle{ i\neq j }[/math], we take union of [math]\displaystyle{ S_i }[/math] and [math]\displaystyle{ S_j }[/math]. The edges in the contracted multi-graph are the edges that cross between different vertex classes.

This view of contraction is illustrated by the following picture:

The following claim is left as an exercise for the class:

With suitable choice of data structures, each operation [math]\displaystyle{ Contract(G,e) }[/math] can be implemented within running time [math]\displaystyle{ O(n) }[/math] where [math]\displaystyle{ n=|V| }[/math] is the number of vertices.

In the above RandomContract algorithm, there are precisely [math]\displaystyle{ n-2 }[/math] contractions. Therefore, we have the following time upper bound.

Theorem

The time of a single running of the RandomContract algorithm is bounded by [math]\displaystyle{ O(n^2) }[/math].

The reason that here we emphasize it's a "single running" will be clear later: because we may run this algorithm for many times to guarantee a desirable accuracy.

Analysis of accuracy

We now analyze the performance of the above algorithm. Since the algorithm is randomized, its output cut is a random variable even when the input is fixed, so the output may not always be correct. We want to give a theoretical guarantee of the chance that the algorithm returns a correct answer on an arbitrary input.

More precisely, on an arbitrarily fixed input multi-graph [math]\displaystyle{ G }[/math], we want to answer the following question rigorously:

[math]\displaystyle{ p_{{correct}}=\Pr[\,\mbox{a minimum cut is returned by \emph{RandomContract}}\,]\ge ? }[/math]

To answer this question, we prove a stronger statement: for arbitrarily fixed input multi-graph [math]\displaystyle{ G }[/math] and a particular minimum cut [math]\displaystyle{ C }[/math] in [math]\displaystyle{ G }[/math],

[math]\displaystyle{ p_{C}=\Pr[\,C\mbox{ is returned by \emph{RandomContract}}\,]\ge ? }[/math]

Obviously this will imply the previous lower bound for [math]\displaystyle{ p_{\text{correct}} }[/math] because the event in [math]\displaystyle{ p_{C} }[/math] implies the event in [math]\displaystyle{ p_{\text{correct}} }[/math].

Let [math]\displaystyle{ e_1,e_2,\ldots,e_{n-2} }[/math] denote the sequence of random edges chosen to contract in a running of RandomContract algorithm. Obviously [math]\displaystyle{ e_1,e_2,\ldots,e_{n-2} }[/math] are random variables, and they are the only random choices used in the algorithm: meaning that they uniquely determine the current multi-graph in every iteration of the algorithm as well as the final output.

We now want to compute the probability [math]\displaystyle{ p_C }[/math] by decompose it into more elementary events involving [math]\displaystyle{ e_1,e_2,\ldots,e_{n-2} }[/math]. This is due to the following proposition.

Proposition

If [math]\displaystyle{ C }[/math] is a minimum cut in a multi-graph [math]\displaystyle{ G }[/math] and [math]\displaystyle{ e\not\in C }[/math], then [math]\displaystyle{ C }[/math] is still a minimum cut in the contracted graph [math]\displaystyle{ G'=contract(G,e) }[/math].

Proof. We first observe that contraction will never create new cuts: every cut in the contracted graph [math]\displaystyle{ G' }[/math] must also be a cut in the original graph [math]\displaystyle{ G }[/math]. We then observe that a cut [math]\displaystyle{ C }[/math] in [math]\displaystyle{ G }[/math] "survives" in the contracted graph [math]\displaystyle{ G' }[/math] if and only if the contracted edge [math]\displaystyle{ e\not\in C }[/math]. Both observations are easy to verify by the definition of contraction operator (in particular, easier to verify if we take the vertex class interpretation). The detailed proofs are left as an exercise. [math]\displaystyle{ \square }[/math]

Recall that [math]\displaystyle{ e_1,e_2,\ldots,e_{n-2} }[/math] denote the sequence of random edges chosen to contract in a running of RandomContract algorithm.

By the above proposition, the event [math]\displaystyle{ C\mbox{ is returned by \emph{RandomContract}} }[/math] is equivalent to the event [math]\displaystyle{ e_i\not\in C\mbox{ for all }i=1,2,\ldots,n-2 }[/math]. Therefore:

[math]\displaystyle{ \begin{align} p_C &= \Pr[\,C\mbox{ is returned by \emph{RandomContract}}\,]\\ &= \Pr[\,e_i\not\in C\mbox{ for all }i=1,2,\ldots,n-2\,]\\ &= \prod_{i=1}^{n-2}\Pr[e_i\not\in C\mid \forall j\lt i, e_j\not\in C]. \end{align} }[/math]

The last equation is due to the so called chain rule in probability.

Lemma 3

If [math]\displaystyle{ C }[/math] is a min-cut in a multi-graph [math]\displaystyle{ G(V,E) }[/math], then [math]\displaystyle{ |E|\ge \frac{|V||C|}{2} }[/math].

Proof. It must hold that the degree of each vertex [math]\displaystyle{ v\in V }[/math] is at least [math]\displaystyle{ |C| }[/math], or otherwise the set of adjacent edges of [math]\displaystyle{ v }[/math] forms a cut which separates [math]\displaystyle{ v }[/math] from the rest of [math]\displaystyle{ V }[/math] and has size less than [math]\displaystyle{ |C| }[/math], contradicting the assumption that [math]\displaystyle{ |C| }[/math] is a min-cut. And the bound [math]\displaystyle{ |E|\ge \frac{|V||C|}{2} }[/math] follows directly from the fact that every vertex in [math]\displaystyle{ G }[/math] has degree at least [math]\displaystyle{ |C| }[/math]. [math]\displaystyle{ \square }[/math]

For a multigraph [math]\displaystyle{ G(V, E) }[/math], fixed a minimum cut [math]\displaystyle{ C }[/math] (there might be more than one minimum cuts), we analyze the probability that [math]\displaystyle{ C }[/math] is returned by the above algorithm.

Initially [math]\displaystyle{ |V|=n }[/math]. We say that the min-cut [math]\displaystyle{ C }[/math] "survives" a random contraction if none of the edges in [math]\displaystyle{ C }[/math] is chosen to be contracted. After [math]\displaystyle{ (i-1) }[/math] contractions, denote the current multigraph as [math]\displaystyle{ G_i(V_i, E_i) }[/math]. Supposed that [math]\displaystyle{ C }[/math] survives the first [math]\displaystyle{ (i-1) }[/math] contractions, according to Lemma 1 and 2, [math]\displaystyle{ C }[/math] must be a minimum cut in the current multi-graph [math]\displaystyle{ G_i }[/math]. Then due to Lemma 3, the current edge number is [math]\displaystyle{ |E_i|\ge |V_i||C|/2 }[/math]. Uniformly choosing an edge [math]\displaystyle{ e\in E_i }[/math] to contract, the probability that the [math]\displaystyle{ i }[/math]th contraction contracts an edge in [math]\displaystyle{ C }[/math] is given by:

[math]\displaystyle{ \begin{align}\Pr_{e\in E_i}[e\in C] &= \frac{|C|}{|E_i|} &\le |C|\cdot\frac{2}{|V_i||C|} &= \frac{2}{|V_i|}.\end{align} }[/math]

Therefore, conditioning on that [math]\displaystyle{ C }[/math] survives the first [math]\displaystyle{ (i-1) }[/math] contractions, the probability that [math]\displaystyle{ C }[/math] survives the [math]\displaystyle{ i }[/math]th contraction is at least [math]\displaystyle{ 1-2/|V_i| }[/math]. Note that [math]\displaystyle{ |V_i|=n-i+1 }[/math], because each contraction decrease the vertex number by 1.

The probability that no edge in the minimum cut [math]\displaystyle{ C }[/math] is ever contracted is:

[math]\displaystyle{ \begin{align} &\quad\,\prod_{i=1}^{n-2}\Pr[\,C\mbox{ survives all }(n-2)\mbox{ contractions }]\\ &= \prod_{i=1}^{n-2}\Pr[\,C\mbox{ survives the }i\mbox{-th contraction}\mid C\mbox{ survives the first }(i-1)\mbox{-th contractions}]\\ &\ge \prod_{i=1}^{n-2}\left(1-\frac{2}{|V_i|}\right) \\ &= \prod_{i=1}^{n-2}\left(1-\frac{2}{n-i+1}\right)\\ &= \prod_{k=3}^{n}\frac{k-2}{k}\\ &= \frac{2}{n(n-1)}. \end{align} }[/math]

This gives the following theorem.

Theorem

For any multigraph with [math]\displaystyle{ n }[/math] vertices, the RandomContract algorithm returns a minimum cut with probability at least [math]\displaystyle{ \frac{2}{n(n-1)} }[/math].

Run RandomContract independently for [math]\displaystyle{ n(n-1)/2 }[/math] times and return the smallest cut returned. The probability that a minimum cut is found is at least:

[math]\displaystyle{ \begin{align} 1-\Pr[\mbox{failed every time}] &= 1-\Pr[{RandomContract}\mbox{ fails}]^{n(n-1)/2} \\ &\ge 1- \left(1-\frac{2}{n(n-1)}\right)^{n(n-1)/2} \\ &\ge 1-\frac{1}{e}. \end{align} }[/math]

A constant probability!

A Corollary by the Probabilistic Method

Karger's algorithm and its analysis implies the following combinatorial theorem regarding the number of distinct minimum cuts in a graph.

Corollary

For any graph [math]\displaystyle{ G(V,E) }[/math] of [math]\displaystyle{ n }[/math] vertices, the number of distinct minimum cuts in [math]\displaystyle{ G }[/math] is at most [math]\displaystyle{ \frac{n(n-2)}{2} }[/math].

Proof. For each minimum cut [math]\displaystyle{ C }[/math] in [math]\displaystyle{ G }[/math], we define [math]\displaystyle{ \mathcal{E}_C }[/math] to be the event that RandomContract returns [math]\displaystyle{ C }[/math]. Due to the analysis of RandomContract, [math]\displaystyle{ \Pr[\mathcal{E}_C]\ge \frac{2}{n(n-1)} }[/math]. The events [math]\displaystyle{ \mathcal{E}_C }[/math] are mutually disjoint for distinct [math]\displaystyle{ C }[/math] and the event that RandomContract returns a min-cut is the disjoint union of [math]\displaystyle{ \mathcal{E}_C }[/math] over all min-cut [math]\displaystyle{ C }[/math]. Therefore, [math]\displaystyle{ \begin{align} &\Pr[\mbox{ RandomContract returns a min-cut}]\\ = &\sum_{\mbox{min-cut }C\mbox{ in }G}\Pr[\mathcal{E}_C]\\ \ge &\sum_{\mbox{min-cut }C\mbox{ in }G}\frac{2}{n(n-1)}, \end{align} }[/math] which must be no greater than 1 for a well-defined probability space. This means the total number of min-cut in [math]\displaystyle{ G }[/math] must be no greater than [math]\displaystyle{ \frac{n(n-1)}{2} }[/math]. [math]\displaystyle{ \square }[/math]

Note that the statement of this theorem has no randomness at all, however the proof involves a randomized algorithm. This is an example of the probabilistic method.

Fast Min-Cut

In the analysis of RandomContract, we have the following observation:

• The probability of success is only getting worse when the graph becomes small.

This motivates us to consider the following alternation to the algorithm: first using random contractions to reduce the number of vertices to a moderately small number, and then recursively finding a min-cut in this smaller instance. This seems just a restatement of exactly what we have been doing. Inspired by the idea of boosting the accuracy via independent repetition, here we apply the recursion on two smaller instances generated independently.

The algorithm obtained in this way is called FastCut. We first define a procedure to randomly contract edges until there are [math]\displaystyle{ t }[/math] number of vertices left.

RandomContract[math]\displaystyle{ (G, t) }[/math]

while [math]\displaystyle{ |V|\gt t }[/math] do choose an edge [math]\displaystyle{ uv\in E }[/math] uniformly at random; [math]\displaystyle{ G=contract(G,uv) }[/math]; return [math]\displaystyle{ G }[/math];

The FastCut algorithm is recursively defined as follows.

FastCut[math]\displaystyle{ (G) }[/math]

if [math]\displaystyle{ |V|\le 6 }[/math] then return a mincut by brute force; else let [math]\displaystyle{ t=\left\lceil1+|V|/\sqrt{2}\right\rceil }[/math]; [math]\displaystyle{ G_1=RandomContract(G,t) }[/math]; [math]\displaystyle{ G_2=RandomContract(G,t) }[/math]; return the smaller one of [math]\displaystyle{ FastCut(G_1) }[/math] and [math]\displaystyle{ FastCut(G_2) }[/math];

As before, all [math]\displaystyle{ G }[/math] are multigraphs.

Let [math]\displaystyle{ C }[/math] be a min-cut in the original multigraph [math]\displaystyle{ G }[/math]. By the same analysis as in the case of RandomContract, we have

[math]\displaystyle{ \begin{align} &\Pr[C\text{ survives all contractions in }RandomContract(G,t)]\\ = &\prod_{i=1}^{n-t}\Pr[C\text{ survives the }i\text{-th contraction}\mid C\text{ survives the first }(i-1)\text{-th contractions}]\\ \ge &\prod_{i=1}^{n-t}\left(1-\frac{2}{n-i+1}\right)\\ = &\prod_{k=t+1}^{n}\frac{k-2}{k}\\ = &\frac{t(t-1)}{n(n-1)}. \end{align} }[/math]

When [math]\displaystyle{ t=\left\lceil1+n/\sqrt{2}\right\rceil }[/math], this probability is at least [math]\displaystyle{ 1/2 }[/math].

We use [math]\displaystyle{ p(n) }[/math] to denote the probability that [math]\displaystyle{ C }[/math] is returned by [math]\displaystyle{ FastCut(G) }[/math], where [math]\displaystyle{ G }[/math] is a multigraph of [math]\displaystyle{ n }[/math] vertices. We then have the following recursion for [math]\displaystyle{ p(n) }[/math].

[math]\displaystyle{ \begin{align} p(n) &= \Pr[C\text{ is returned by }\textit{FastCut}(G)]\\ &= 1-\left(1-\Pr[C\text{ survives in }G_1\wedge C=\textit{FastCut}(G_1)]\right)^2\\ &= 1-\left(1-\Pr[C\text{ survives in }G_1]\Pr[C=\textit{FastCut}(G_1)\mid C\text{ survives in }G_1]\right)^2\\ &\ge 1-\left(1-\frac{1}{2}p\left(\left\lceil1+n/\sqrt{2}\right\rceil\right)\right)^2, \end{align} }[/math]

where the last inequality is due to the fact that [math]\displaystyle{ \Pr[C\text{ survives all contractions in }RandomContract(G,t)]\ge1/2 }[/math] and our previous discussions in the analysis of RandomContract that if the min-cut [math]\displaystyle{ C }[/math] survives all first [math]\displaystyle{ (n-t) }[/math] contractions then [math]\displaystyle{ C }[/math] must be a min-cut in the remaining multigraph.

The base case is that [math]\displaystyle{ p(n)=1 }[/math] for [math]\displaystyle{ n\le 6 }[/math]. Solving this recursion of [math]\displaystyle{ p(n) }[/math] (or proving by induction) gives us that

[math]\displaystyle{ p(n)=\Omega\left(\frac{1}{\log n}\right). }[/math]

Recall that we can implement an edge contraction in [math]\displaystyle{ O(n) }[/math] time, thus it is easy to verify the following recursion of time complexity:

[math]\displaystyle{ T(n)=2T\left(\left\lceil1+n/\sqrt{2}\right\rceil\right)+O(n^2), }[/math]

where [math]\displaystyle{ T(n) }[/math] denotes the running time of [math]\displaystyle{ FastCut(G) }[/math] on a multigraph [math]\displaystyle{ G }[/math] of [math]\displaystyle{ n }[/math] vertices.

Solving the recursion of [math]\displaystyle{ T(n) }[/math] with the base case [math]\displaystyle{ T(n)=O(1) }[/math] for [math]\displaystyle{ n\le 6 }[/math], we have [math]\displaystyle{ T(n)=O(n^2\log n) }[/math].

Therefore, for a multigraph [math]\displaystyle{ G }[/math] of [math]\displaystyle{ n }[/math] vertices, the algorithm [math]\displaystyle{ FastCut(G) }[/math] returns a min-cut in [math]\displaystyle{ G }[/math] with probability [math]\displaystyle{ \Omega\left(\frac{1}{\log n}\right) }[/math] in time [math]\displaystyle{ O(n^2\log n) }[/math]. Repeat this independently for [math]\displaystyle{ O(log n) }[/math] times, we have an algorithm which runs in time [math]\displaystyle{ O(n^2\log^2n) }[/math] and returns a min-cut with probability [math]\displaystyle{ 1-O(1/n) }[/math], a high probability.