高级算法 (Fall 2019)/Concentration of measure: Difference between revisions
imported>Etone |
imported>Etone |
||
| Line 247: | Line 247: | ||
The purpose of this generalization is that we are usually more interested in a function of a sequence of random variables, rather than the sequence itself. | The purpose of this generalization is that we are usually more interested in a function of a sequence of random variables, rather than the sequence itself. | ||
=Azuma's Inequality= | |||
We introduce a martingale tail inequality, called Azuma's inequality. | |||
{{Theorem | |||
|Azuma's Inequality| | |||
:Let <math>X_0,X_1,\ldots</math> be a martingale such that, for all <math>k\ge 1</math>, | |||
::<math> | |||
|X_{k}-X_{k-1}|\le c_k, | |||
</math> | |||
:Then | |||
::<math>\begin{align} | |||
\Pr\left[|X_n-X_0|\ge t\right]\le 2\exp\left(-\frac{t^2}{2\sum_{k=1}^nc_k^2}\right). | |||
\end{align}</math> | |||
}} | |||
Before formally proving this theorem, some comments are in order. First, unlike the Chernoff bounds, there is no assumption of independence. This shows the power of martingale inequalities. | |||
Second, the condition that | |||
:<math> | |||
|X_{k}-X_{k-1}|\le c_k | |||
</math> | |||
is central to the proof. This condition is sometimes called the '''bounded difference condition'''. If we think of the martingale <math>X_0,X_1,\ldots</math> as a process evolving through time, where <math>X_i</math> gives some measurement at time <math>i</math>, the bounded difference condition states that the process does not make big jumps. The Azuma's inequality says that if so, then it is unlikely that process wanders far from its starting point. | |||
A special case is when the differences are bounded by a constant. The following corollary is directly implied by the Azuma's inequality. | |||
{{Theorem | |||
|Corollary| | |||
:Let <math>X_0,X_1,\ldots</math> be a martingale such that, for all <math>k\ge 1</math>, | |||
::<math> | |||
|X_{k}-X_{k-1}|\le c, | |||
</math> | |||
:Then | |||
::<math>\begin{align} | |||
\Pr\left[|X_n-X_0|\ge ct\sqrt{n}\right]\le 2 e^{-t^2/2}. | |||
\end{align}</math> | |||
}} | |||
This corollary states that for any martingale sequence whose diferences are bounded by a constant, the probability that it deviates <math>\omega(\sqrt{n})</math> far away from the starting point after <math>n</math> steps is bounded by <math>o(1)</math>. | |||
=== Generalization === | |||
Azuma's inequality can be generalized to a martingale with respect another sequence. | |||
{{Theorem | |||
|Azuma's Inequality (general version)| | |||
:Let <math>Y_0,Y_1,\ldots</math> be a martingale with respect to the sequence <math>X_0,X_1,\ldots</math> such that, for all <math>k\ge 1</math>, | |||
::<math> | |||
|Y_{k}-Y_{k-1}|\le c_k, | |||
</math> | |||
:Then | |||
::<math>\begin{align} | |||
\Pr\left[|Y_n-Y_0|\ge t\right]\le 2\exp\left(-\frac{t^2}{2\sum_{k=1}^nc_k^2}\right). | |||
\end{align}</math> | |||
}} | |||
=== The Proof of Azuma's Inueqality=== | |||
We will only give the formal proof of the non-generalized version. The proof of the general version is almost identical, with the only difference that we work on random sequence <math>Y_i</math> conditioning on sequence <math>X_i</math>. | |||
The proof of Azuma's Inequality uses several ideas which are used in the proof of the Chernoff bounds. We first observe that the total deviation of the martingale sequence can be represented as the sum of deferences in every steps. Thus, as the Chernoff bounds, we are looking for a bound of the deviation of the sum of random variables. The strategy of the proof is almost the same as the proof of Chernoff bounds: we first apply Markov's inequality to the moment generating function, then we bound the moment generating function, and at last we optimize the parameter of the moment generating function. However, unlike the Chernoff bounds, the martingale differences are not independent any more. So we replace the use of the independence in the Chernoff bound by the martingale property. The proof is detailed as follows. | |||
In order to bound the probability of <math>|X_n-X_0|\ge t</math>, we first bound the upper tail <math>\Pr[X_n-X_0\ge t]</math>. The bound of the lower tail can be symmetrically proved with the <math>X_i</math> replaced by <math>-X_i</math>. | |||
==== Represent the deviation as the sum of differences ==== | |||
We define the '''martingale difference sequence''': for <math>i\ge 1</math>, let | |||
:<math> | |||
Y_i=X_i-X_{i-1}. | |||
</math> | |||
It holds that | |||
:<math> | |||
\begin{align} | |||
\mathbf{E}[Y_i\mid X_0,\ldots,X_{i-1}] | |||
&=\mathbf{E}[X_i-X_{i-1}\mid X_0,\ldots,X_{i-1}]\\ | |||
&=\mathbf{E}[X_i\mid X_0,\ldots,X_{i-1}]-\mathbf{E}[X_{i-1}\mid X_0,\ldots,X_{i-1}]\\ | |||
&=X_{i-1}-X_{i-1}\\ | |||
&=0. | |||
\end{align} | |||
</math> | |||
The second to the last equation is due to the fact that <math>X_0,X_1,\ldots</math> is a martingale and the definition of conditional expectation. | |||
Let <math>Z_n</math> be the accumulated differences | |||
:<math> | |||
Z_n=\sum_{i=1}^n Y_i. | |||
</math> | |||
The deviation <math>(X_n-X_0)</math> can be computed by the accumulated differences: | |||
:<math> | |||
\begin{align} | |||
X_n-X_0 | |||
&=(X_1-X_{0})+(X_2-X_1)+\cdots+(X_n-X_{n-1})\\ | |||
&=\sum_{i=1}^n Y_i\\ | |||
&=Z_n. | |||
\end{align} | |||
</math> | |||
We then only need to upper bound the probability of the event <math>Z_n\ge t</math>. | |||
==== Apply Markov's inequality to the moment generating function ==== | |||
The event <math>Z_n\ge t</math> is equivalent to that <math>e^{\lambda Z_n}\ge e^{\lambda t}</math> for <math>\lambda>0</math>. Apply Markov's inequality, we have | |||
:<math> | |||
\begin{align} | |||
\Pr\left[Z_n\ge t\right] | |||
&=\Pr\left[e^{\lambda Z_n}\ge e^{\lambda t}\right]\\ | |||
&\le \frac{\mathbf{E}\left[e^{\lambda Z_n}\right]}{e^{\lambda t}}. | |||
\end{align} | |||
</math> | |||
This is exactly the same as what we did to prove the Chernoff bound. Next, we need to bound the moment generating function <math>\mathbf{E}\left[e^{\lambda Z_n}\right]</math>. | |||
==== Bound the moment generating functions ==== | |||
The moment generating function | |||
:<math> | |||
\begin{align} | |||
\mathbf{E}\left[e^{\lambda Z_n}\right] | |||
&=\mathbf{E}\left[\mathbf{E}\left[e^{\lambda Z_n}\mid X_0,\ldots,X_{n-1}\right]\right]\\ | |||
&=\mathbf{E}\left[\mathbf{E}\left[e^{\lambda (Z_{n-1}+Y_n)}\mid X_0,\ldots,X_{n-1}\right]\right]\\ | |||
&=\mathbf{E}\left[\mathbf{E}\left[e^{\lambda Z_{n-1}}\cdot e^{\lambda Y_n}\mid X_0,\ldots,X_{n-1}\right]\right]\\ | |||
&=\mathbf{E}\left[e^{\lambda Z_{n-1}}\cdot\mathbf{E}\left[e^{\lambda Y_n}\mid X_0,\ldots,X_{n-1}\right]\right] | |||
\end{align} | |||
</math> | |||
The first and the last equations are due to the fundamental facts about conditional expectation which are proved by us in the first section. | |||
We then upper bound the <math>\mathbf{E}\left[e^{\lambda Y_n}\mid X_0,\ldots,X_{n-1}\right]</math> by a constant. To do so, we need the following technical lemma which is proved by the convexity of <math>e^{\lambda Y_n}</math>. | |||
{{Theorem | |||
|Lemma| | |||
:Let <math>X</math> be a random variable such that <math>\mathbf{E}[X]=0</math> and <math>|X|\le c</math>. Then for <math>\lambda>0</math>, | |||
::<math> | |||
\mathbf{E}[e^{\lambda X}]\le e^{\lambda^2c^2/2}. | |||
</math> | |||
}} | |||
{{Proof| Observe that for <math>\lambda>0</math>, the function <math>e^{\lambda X}</math> of the variable <math>X</math> is convex in the interval <math>[-c,c]</math>. We draw a line between the two endpoints points <math>(-c, e^{-\lambda c})</math> and <math>(c, e^{\lambda c})</math>. The curve of <math>e^{\lambda X}</math> lies entirely below this line. Thus, | |||
:<math> | |||
\begin{align} | |||
e^{\lambda X} | |||
&\le \frac{c-X}{2c}e^{-\lambda c}+\frac{c+X}{2c}e^{\lambda c}\\ | |||
&=\frac{e^{\lambda c}+e^{-\lambda c}}{2}+\frac{X}{2c}(e^{\lambda c}-e^{-\lambda c}). | |||
\end{align} | |||
</math> | |||
Since <math>\mathbf{E}[X]=0</math>, we have | |||
:<math> | |||
\begin{align} | |||
\mathbf{E}[e^{\lambda X}] | |||
&\le \mathbf{E}[\frac{e^{\lambda c}+e^{-\lambda c}}{2}+\frac{X}{2c}(e^{\lambda c}-e^{-\lambda c})]\\ | |||
&=\frac{e^{\lambda c}+e^{-\lambda c}}{2}+\frac{e^{\lambda c}-e^{-\lambda c}}{2c}\mathbf{E}[X]\\ | |||
&=\frac{e^{\lambda c}+e^{-\lambda c}}{2}. | |||
\end{align} | |||
</math> | |||
By expanding both sides as Taylor's series, it can be verified that <math>\frac{e^{\lambda c}+e^{-\lambda c}}{2}\le e^{\lambda^2c^2/2}</math>. | |||
}} | |||
Apply the above lemma to the random variable | |||
:<math> | |||
(Y_n \mid X_0,\ldots,X_{n-1}) | |||
</math> | |||
We have already shown that its expectation | |||
<math> | |||
\mathbf{E}[(Y_n \mid X_0,\ldots,X_{n-1})]=0, | |||
</math> | |||
and by the bounded difference condition of Azuma's inequality, we have | |||
<math> | |||
|Y_n|=|(X_n-X_{n-1})|\le c_n. | |||
</math> | |||
Thus, due to the above lemma, it holds that | |||
:<math> | |||
\mathbf{E}[e^{\lambda Y_n}\mid X_0,\ldots,X_{n-1}]\le e^{\lambda^2c_n^2/2}. | |||
</math> | |||
Back to our analysis of the expectation <math>\mathbf{E}\left[e^{\lambda Z_n}\right]</math>, we have | |||
:<math> | |||
\begin{align} | |||
\mathbf{E}\left[e^{\lambda Z_n}\right] | |||
&=\mathbf{E}\left[e^{\lambda Z_{n-1}}\cdot\mathbf{E}\left[e^{\lambda Y_n}\mid X_0,\ldots,X_{n-1}\right]\right]\\ | |||
&\le \mathbf{E}\left[e^{\lambda Z_{n-1}}\cdot e^{\lambda^2c_n^2/2}\right]\\ | |||
&= e^{\lambda^2c_n^2/2}\cdot\mathbf{E}\left[e^{\lambda Z_{n-1}}\right] . | |||
\end{align} | |||
</math> | |||
Apply the same analysis to <math>\mathbf{E}\left[e^{\lambda Z_{n-1}}\right]</math>, we can solve the above recursion by | |||
:<math> | |||
\begin{align} | |||
\mathbf{E}\left[e^{\lambda Z_n}\right] | |||
&\le \prod_{k=1}^n e^{\lambda^2c_k^2/2}\\ | |||
&= \exp\left(\lambda^2\sum_{k=1}^n c_k^2/2\right). | |||
\end{align} | |||
</math> | |||
Go back to the Markov's inequality, | |||
:<math> | |||
\begin{align} | |||
\Pr\left[Z_n\ge t\right] | |||
&\le \frac{\mathbf{E}\left[e^{\lambda Z_n}\right]}{e^{\lambda t}}\\ | |||
&\le \exp\left(\lambda^2\sum_{k=1}^n c_k^2/2-\lambda t\right). | |||
\end{align} | |||
</math> | |||
We then only need to choose a proper <math>\lambda>0</math>. | |||
==== Optimization ==== | |||
By choosing <math>\lambda=\frac{t}{\sum_{k=1}^n c_k^2}</math>, we have that | |||
:<math> | |||
\exp\left(\lambda^2\sum_{k=1}^n c_k^2/2-\lambda t\right)=\exp\left(-\frac{t^2}{2\sum_{k=1}^n c_k^2}\right). | |||
</math> | |||
Thus, the probability | |||
:<math> | |||
\begin{align} | |||
\Pr\left[X_n-X_0\ge t\right] | |||
&=\Pr\left[Z_n\ge t\right]\\ | |||
&\le \exp\left(\lambda^2\sum_{k=1}^n c_k^2/2-\lambda t\right)\\ | |||
&= \exp\left(-\frac{t^2}{2\sum_{k=1}^n c_k^2}\right). | |||
\end{align} | |||
</math> | |||
The upper tail of Azuma's inequality is proved. By replacing <math>X_i</math> by <math>-X_i</math>, the lower tail can be treated just as the upper tail. Applying the union bound, Azuma's inequality is proved. | |||
Revision as of 06:02, 8 October 2019
Chernoff Bound
Suppose that we have a fair coin. If we toss it once, then the outcome is completely unpredictable. But if we toss it, say for 1000 times, then the number of HEADs is very likely to be around 500. This phenomenon, as illustrated in the following figure, is called the concentration of measure. The Chernoff bound is an inequality that characterizes the concentration phenomenon for the sum of independent trials.
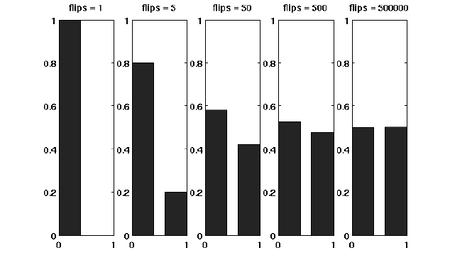
Before formally stating the Chernoff bound, let's introduce the moment generating function.
Moment generating functions
The more we know about the moments of a random variable [math]\displaystyle{ X }[/math], the more information we would have about [math]\displaystyle{ X }[/math]. There is a so-called moment generating function, which "packs" all the information about the moments of [math]\displaystyle{ X }[/math] into one function.
Definition - The moment generating function of a random variable [math]\displaystyle{ X }[/math] is defined as [math]\displaystyle{ \mathbf{E}\left[\mathrm{e}^{\lambda X}\right] }[/math] where [math]\displaystyle{ \lambda }[/math] is the parameter of the function.
By Taylor's expansion and the linearity of expectations,
- [math]\displaystyle{ \begin{align} \mathbf{E}\left[\mathrm{e}^{\lambda X}\right] &= \mathbf{E}\left[\sum_{k=0}^\infty\frac{\lambda^k}{k!}X^k\right]\\ &=\sum_{k=0}^\infty\frac{\lambda^k}{k!}\mathbf{E}\left[X^k\right] \end{align} }[/math]
The moment generating function [math]\displaystyle{ \mathbf{E}\left[\mathrm{e}^{\lambda X}\right] }[/math] is a function of [math]\displaystyle{ \lambda }[/math].
The Chernoff bound
The Chernoff bounds are exponentially sharp tail inequalities for the sum of independent trials. The bounds are obtained by applying Markov's inequality to the moment generating function of the sum of independent trials, with some appropriate choice of the parameter [math]\displaystyle{ \lambda }[/math].
Chernoff bound (the upper tail) - Let [math]\displaystyle{ X=\sum_{i=1}^n X_i }[/math], where [math]\displaystyle{ X_1, X_2, \ldots, X_n }[/math] are independent Poisson trials. Let [math]\displaystyle{ \mu=\mathbf{E}[X] }[/math].
- Then for any [math]\displaystyle{ \delta\gt 0 }[/math],
- [math]\displaystyle{ \Pr[X\ge (1+\delta)\mu]\le\left(\frac{e^{\delta}}{(1+\delta)^{(1+\delta)}}\right)^{\mu}. }[/math]
Proof. For any [math]\displaystyle{ \lambda\gt 0 }[/math], [math]\displaystyle{ X\ge (1+\delta)\mu }[/math] is equivalent to that [math]\displaystyle{ e^{\lambda X}\ge e^{\lambda (1+\delta)\mu} }[/math], thus - [math]\displaystyle{ \begin{align} \Pr[X\ge (1+\delta)\mu] &= \Pr\left[e^{\lambda X}\ge e^{\lambda (1+\delta)\mu}\right]\\ &\le \frac{\mathbf{E}\left[e^{\lambda X}\right]}{e^{\lambda (1+\delta)\mu}}, \end{align} }[/math]
where the last step follows by Markov's inequality.
Computing the moment generating function [math]\displaystyle{ \mathbf{E}[e^{\lambda X}] }[/math]:
- [math]\displaystyle{ \begin{align} \mathbf{E}\left[e^{\lambda X}\right] &= \mathbf{E}\left[e^{\lambda \sum_{i=1}^n X_i}\right]\\ &= \mathbf{E}\left[\prod_{i=1}^n e^{\lambda X_i}\right]\\ &= \prod_{i=1}^n \mathbf{E}\left[e^{\lambda X_i}\right]. & (\mbox{for independent random variables}) \end{align} }[/math]
Let [math]\displaystyle{ p_i=\Pr[X_i=1] }[/math] for [math]\displaystyle{ i=1,2,\ldots,n }[/math]. Then,
- [math]\displaystyle{ \mu=\mathbf{E}[X]=\mathbf{E}\left[\sum_{i=1}^n X_i\right]=\sum_{i=1}^n\mathbf{E}[X_i]=\sum_{i=1}^n p_i }[/math].
We bound the moment generating function for each individual [math]\displaystyle{ X_i }[/math] as follows.
- [math]\displaystyle{ \begin{align} \mathbf{E}\left[e^{\lambda X_i}\right] &= p_i\cdot e^{\lambda\cdot 1}+(1-p_i)\cdot e^{\lambda\cdot 0}\\ &= 1+p_i(e^\lambda -1)\\ &\le e^{p_i(e^\lambda-1)}, \end{align} }[/math]
where in the last step we apply the Taylor's expansion so that [math]\displaystyle{ e^y\ge 1+y }[/math] where [math]\displaystyle{ y=p_i(e^\lambda-1)\ge 0 }[/math]. (By doing this, we can transform the product to the sum of [math]\displaystyle{ p_i }[/math], which is [math]\displaystyle{ \mu }[/math].)
Therefore,
- [math]\displaystyle{ \begin{align} \mathbf{E}\left[e^{\lambda X}\right] &= \prod_{i=1}^n \mathbf{E}\left[e^{\lambda X_i}\right]\\ &\le \prod_{i=1}^n e^{p_i(e^\lambda-1)}\\ &= \exp\left(\sum_{i=1}^n p_i(e^{\lambda}-1)\right)\\ &= e^{(e^\lambda-1)\mu}. \end{align} }[/math]
Thus, we have shown that for any [math]\displaystyle{ \lambda\gt 0 }[/math],
- [math]\displaystyle{ \begin{align} \Pr[X\ge (1+\delta)\mu] &\le \frac{\mathbf{E}\left[e^{\lambda X}\right]}{e^{\lambda (1+\delta)\mu}}\\ &\le \frac{e^{(e^\lambda-1)\mu}}{e^{\lambda (1+\delta)\mu}}\\ &= \left(\frac{e^{(e^\lambda-1)}}{e^{\lambda (1+\delta)}}\right)^\mu \end{align} }[/math].
For any [math]\displaystyle{ \delta\gt 0 }[/math], we can let [math]\displaystyle{ \lambda=\ln(1+\delta)\gt 0 }[/math] to get
- [math]\displaystyle{ \Pr[X\ge (1+\delta)\mu]\le\left(\frac{e^{\delta}}{(1+\delta)^{(1+\delta)}}\right)^{\mu}. }[/math]
- [math]\displaystyle{ \square }[/math]
The idea of the proof is actually quite clear: we apply Markov's inequality to [math]\displaystyle{ e^{\lambda X} }[/math] and for the rest, we just estimate the moment generating function [math]\displaystyle{ \mathbf{E}[e^{\lambda X}] }[/math]. To make the bound as tight as possible, we minimized the [math]\displaystyle{ \frac{e^{(e^\lambda-1)}}{e^{\lambda (1+\delta)}} }[/math] by setting [math]\displaystyle{ \lambda=\ln(1+\delta) }[/math], which can be justified by taking derivatives of [math]\displaystyle{ \frac{e^{(e^\lambda-1)}}{e^{\lambda (1+\delta)}} }[/math].
We then proceed to the lower tail, the probability that the random variable deviates below the mean value:
Chernoff bound (the lower tail) - Let [math]\displaystyle{ X=\sum_{i=1}^n X_i }[/math], where [math]\displaystyle{ X_1, X_2, \ldots, X_n }[/math] are independent Poisson trials. Let [math]\displaystyle{ \mu=\mathbf{E}[X] }[/math].
- Then for any [math]\displaystyle{ 0\lt \delta\lt 1 }[/math],
- [math]\displaystyle{ \Pr[X\le (1-\delta)\mu]\le\left(\frac{e^{-\delta}}{(1-\delta)^{(1-\delta)}}\right)^{\mu}. }[/math]
Proof. For any [math]\displaystyle{ \lambda\lt 0 }[/math], by the same analysis as in the upper tail version, - [math]\displaystyle{ \begin{align} \Pr[X\le (1-\delta)\mu] &= \Pr\left[e^{\lambda X}\ge e^{\lambda (1-\delta)\mu}\right]\\ &\le \frac{\mathbf{E}\left[e^{\lambda X}\right]}{e^{\lambda (1-\delta)\mu}}\\ &\le \left(\frac{e^{(e^\lambda-1)}}{e^{\lambda (1-\delta)}}\right)^\mu. \end{align} }[/math]
For any [math]\displaystyle{ 0\lt \delta\lt 1 }[/math], we can let [math]\displaystyle{ \lambda=\ln(1-\delta)\lt 0 }[/math] to get
- [math]\displaystyle{ \Pr[X\ge (1-\delta)\mu]\le\left(\frac{e^{-\delta}}{(1-\delta)^{(1-\delta)}}\right)^{\mu}. }[/math]
- [math]\displaystyle{ \square }[/math]
Useful forms of the Chernoff bounds
Some useful special forms of the bounds can be derived directly from the above general forms of the bounds. We now know better why we say that the bounds are exponentially sharp.
Useful forms of the Chernoff bound - Let [math]\displaystyle{ X=\sum_{i=1}^n X_i }[/math], where [math]\displaystyle{ X_1, X_2, \ldots, X_n }[/math] are independent Poisson trials. Let [math]\displaystyle{ \mu=\mathbf{E}[X] }[/math]. Then
- 1. for [math]\displaystyle{ 0\lt \delta\le 1 }[/math],
- [math]\displaystyle{ \Pr[X\ge (1+\delta)\mu]\lt \exp\left(-\frac{\mu\delta^2}{3}\right); }[/math]
- [math]\displaystyle{ \Pr[X\le (1-\delta)\mu]\lt \exp\left(-\frac{\mu\delta^2}{2}\right); }[/math]
- 2. for [math]\displaystyle{ t\ge 2e\mu }[/math],
- [math]\displaystyle{ \Pr[X\ge t]\le 2^{-t}. }[/math]
Proof. To obtain the bounds in (1), we need to show that for [math]\displaystyle{ 0\lt \delta\lt 1 }[/math], [math]\displaystyle{ \frac{e^{\delta}}{(1+\delta)^{(1+\delta)}}\le e^{-\delta^2/3} }[/math] and [math]\displaystyle{ \frac{e^{-\delta}}{(1-\delta)^{(1-\delta)}}\le e^{-\delta^2/2} }[/math]. We can verify both inequalities by standard analysis techniques. To obtain the bound in (2), let [math]\displaystyle{ t=(1+\delta)\mu }[/math]. Then [math]\displaystyle{ \delta=t/\mu-1\ge 2e-1 }[/math]. Hence,
- [math]\displaystyle{ \begin{align} \Pr[X\ge(1+\delta)\mu] &\le \left(\frac{e^\delta}{(1+\delta)^{(1+\delta)}}\right)^\mu\\ &\le \left(\frac{e}{1+\delta}\right)^{(1+\delta)\mu}\\ &\le \left(\frac{e}{2e}\right)^t\\ &\le 2^{-t} \end{align} }[/math]
- [math]\displaystyle{ \square }[/math]
Applications to balls-into-bins
Throwing [math]\displaystyle{ m }[/math] balls uniformly and independently to [math]\displaystyle{ n }[/math] bins, what is the maximum load of all bins with high probability? In the last class, we gave an analysis of this problem by using a counting argument.
Now we give a more "advanced" analysis by using Chernoff bounds.
For any [math]\displaystyle{ i\in[n] }[/math] and [math]\displaystyle{ j\in[m] }[/math], let [math]\displaystyle{ X_{ij} }[/math] be the indicator variable for the event that ball [math]\displaystyle{ j }[/math] is thrown to bin [math]\displaystyle{ i }[/math]. Obviously
- [math]\displaystyle{ \mathbf{E}[X_{ij}]=\Pr[\mbox{ball }j\mbox{ is thrown to bin }i]=\frac{1}{n} }[/math]
Let [math]\displaystyle{ Y_i=\sum_{j\in[m]}X_{ij} }[/math] be the load of bin [math]\displaystyle{ i }[/math].
Then the expected load of bin [math]\displaystyle{ i }[/math] is
[math]\displaystyle{ (*)\qquad \mu=\mathbf{E}[Y_i]=\mathbf{E}\left[\sum_{j\in[m]}X_{ij}\right]=\sum_{j\in[m]}\mathbf{E}[X_{ij}]=m/n. }[/math]
For the case [math]\displaystyle{ m=n }[/math], it holds that [math]\displaystyle{ \mu=1 }[/math]
Note that [math]\displaystyle{ Y_i }[/math] is a sum of [math]\displaystyle{ m }[/math] mutually independent indicator variable. Applying Chernoff bound, for any particular bin [math]\displaystyle{ i\in[n] }[/math],
- [math]\displaystyle{ \Pr[Y_i\gt (1+\delta)\mu] \le \left(\frac{e^{\delta}}{(1+\delta)^{1+\delta}}\right)^\mu. }[/math]
The [math]\displaystyle{ m=n }[/math] case
When [math]\displaystyle{ m=n }[/math], [math]\displaystyle{ \mu=1 }[/math]. Write [math]\displaystyle{ c=1+\delta }[/math]. The above bound can be written as
- [math]\displaystyle{ \Pr[Y_i\gt c] \le \frac{e^{c-1}}{c^c}. }[/math]
Let [math]\displaystyle{ c=\frac{e\ln n}{\ln\ln n} }[/math], we evaluate [math]\displaystyle{ \frac{e^{c-1}}{c^c} }[/math] by taking logarithm to its reciprocal.
- [math]\displaystyle{ \begin{align} \ln\left(\frac{c^c}{e^{c-1}}\right) &= c\ln c-c+1\\ &= c(\ln c-1)+1\\ &= \frac{e\ln n}{\ln\ln n}\left(\ln\ln n-\ln\ln\ln n\right)+1\\ &\ge \frac{e\ln n}{\ln\ln n}\cdot\frac{2}{e}\ln\ln n+1\\ &\ge 2\ln n. \end{align} }[/math]
Thus,
- [math]\displaystyle{ \Pr\left[Y_i\gt \frac{e\ln n}{\ln\ln n}\right] \le \frac{1}{n^2}. }[/math]
Applying the union bound, the probability that there exists a bin with load [math]\displaystyle{ \gt 12\ln n }[/math] is
- [math]\displaystyle{ n\cdot \Pr\left[Y_1\gt \frac{e\ln n}{\ln\ln n}\right] \le \frac{1}{n} }[/math].
Therefore, for [math]\displaystyle{ m=n }[/math], with high probability, the maximum load is [math]\displaystyle{ O\left(\frac{e\ln n}{\ln\ln n}\right) }[/math].
The [math]\displaystyle{ m\gt \ln n }[/math] case
When [math]\displaystyle{ m\ge n\ln n }[/math], then according to [math]\displaystyle{ (*) }[/math], [math]\displaystyle{ \mu=\frac{m}{n}\ge \ln n }[/math]
We can apply an easier form of the Chernoff bounds,
- [math]\displaystyle{ \Pr[Y_i\ge 2e\mu]\le 2^{-2e\mu}\le 2^{-2e\ln n}\lt \frac{1}{n^2}. }[/math]
By the union bound, the probability that there exists a bin with load [math]\displaystyle{ \ge 2e\frac{m}{n} }[/math] is,
- [math]\displaystyle{ n\cdot \Pr\left[Y_1\gt 2e\frac{m}{n}\right] = n\cdot \Pr\left[Y_1\gt 2e\mu\right]\le \frac{1}{n} }[/math].
Therefore, for [math]\displaystyle{ m\ge n\ln n }[/math], with high probability, the maximum load is [math]\displaystyle{ O\left(\frac{m}{n}\right) }[/math].
Martingales
"Martingale" originally refers to a betting strategy in which the gambler doubles his bet after every loss. Assuming unlimited wealth, this strategy is guaranteed to eventually have a positive net profit. For example, starting from an initial stake 1, after [math]\displaystyle{ n }[/math] losses, if the [math]\displaystyle{ (n+1) }[/math]th bet wins, then it gives a net profit of
- [math]\displaystyle{ 2^n-\sum_{i=1}^{n}2^{i-1}=1, }[/math]
which is a positive number.
However, the assumption of unlimited wealth is unrealistic. For limited wealth, with geometrically increasing bet, it is very likely to end up bankrupt. You should never try this strategy in real life.
Suppose that the gambler is allowed to use any strategy. His stake on the next beting is decided based on the results of all the bettings so far. This gives us a highly dependent sequence of random variables [math]\displaystyle{ X_0,X_1,\ldots, }[/math], where [math]\displaystyle{ X_0 }[/math] is his initial capital, and [math]\displaystyle{ X_i }[/math] represents his capital after the [math]\displaystyle{ i }[/math]th betting. Up to different betting strategies, [math]\displaystyle{ X_i }[/math] can be arbitrarily dependent on [math]\displaystyle{ X_0,\ldots,X_{i-1} }[/math]. However, as long as the game is fair, namely, winning and losing with equal chances, conditioning on the past variables [math]\displaystyle{ X_0,\ldots,X_{i-1} }[/math], we will expect no change in the value of the present variable [math]\displaystyle{ X_{i} }[/math] on average. Random variables satisfying this property is called a martingale sequence.
Definition (martingale) - A sequence of random variables [math]\displaystyle{ X_0,X_1,\ldots }[/math] is a martingale if for all [math]\displaystyle{ i\gt 0 }[/math],
- [math]\displaystyle{ \begin{align} \mathbf{E}[X_{i}\mid X_0,\ldots,X_{i-1}]=X_{i-1}. \end{align} }[/math]
- A sequence of random variables [math]\displaystyle{ X_0,X_1,\ldots }[/math] is a martingale if for all [math]\displaystyle{ i\gt 0 }[/math],
The martingale can be generalized to be with respect to another sequence of random variables.
Definition (martingale, general version) - A sequence of random variables [math]\displaystyle{ Y_0,Y_1,\ldots }[/math] is a martingale with respect to the sequence [math]\displaystyle{ X_0,X_1,\ldots }[/math] if, for all [math]\displaystyle{ i\ge 0 }[/math], the following conditions hold:
- [math]\displaystyle{ Y_i }[/math] is a function of [math]\displaystyle{ X_0,X_1,\ldots,X_i }[/math];
- [math]\displaystyle{ \begin{align} \mathbf{E}[Y_{i+1}\mid X_0,\ldots,X_{i}]=Y_{i}. \end{align} }[/math]
- A sequence of random variables [math]\displaystyle{ Y_0,Y_1,\ldots }[/math] is a martingale with respect to the sequence [math]\displaystyle{ X_0,X_1,\ldots }[/math] if, for all [math]\displaystyle{ i\ge 0 }[/math], the following conditions hold:
Therefore, a sequence [math]\displaystyle{ X_0,X_1,\ldots }[/math] is a martingale if it is a martingale with respect to itself.
The purpose of this generalization is that we are usually more interested in a function of a sequence of random variables, rather than the sequence itself.
Azuma's Inequality
We introduce a martingale tail inequality, called Azuma's inequality.
Azuma's Inequality - Let [math]\displaystyle{ X_0,X_1,\ldots }[/math] be a martingale such that, for all [math]\displaystyle{ k\ge 1 }[/math],
- [math]\displaystyle{ |X_{k}-X_{k-1}|\le c_k, }[/math]
- Then
- [math]\displaystyle{ \begin{align} \Pr\left[|X_n-X_0|\ge t\right]\le 2\exp\left(-\frac{t^2}{2\sum_{k=1}^nc_k^2}\right). \end{align} }[/math]
- Let [math]\displaystyle{ X_0,X_1,\ldots }[/math] be a martingale such that, for all [math]\displaystyle{ k\ge 1 }[/math],
Before formally proving this theorem, some comments are in order. First, unlike the Chernoff bounds, there is no assumption of independence. This shows the power of martingale inequalities.
Second, the condition that
- [math]\displaystyle{ |X_{k}-X_{k-1}|\le c_k }[/math]
is central to the proof. This condition is sometimes called the bounded difference condition. If we think of the martingale [math]\displaystyle{ X_0,X_1,\ldots }[/math] as a process evolving through time, where [math]\displaystyle{ X_i }[/math] gives some measurement at time [math]\displaystyle{ i }[/math], the bounded difference condition states that the process does not make big jumps. The Azuma's inequality says that if so, then it is unlikely that process wanders far from its starting point.
A special case is when the differences are bounded by a constant. The following corollary is directly implied by the Azuma's inequality.
Corollary - Let [math]\displaystyle{ X_0,X_1,\ldots }[/math] be a martingale such that, for all [math]\displaystyle{ k\ge 1 }[/math],
- [math]\displaystyle{ |X_{k}-X_{k-1}|\le c, }[/math]
- Then
- [math]\displaystyle{ \begin{align} \Pr\left[|X_n-X_0|\ge ct\sqrt{n}\right]\le 2 e^{-t^2/2}. \end{align} }[/math]
- Let [math]\displaystyle{ X_0,X_1,\ldots }[/math] be a martingale such that, for all [math]\displaystyle{ k\ge 1 }[/math],
This corollary states that for any martingale sequence whose diferences are bounded by a constant, the probability that it deviates [math]\displaystyle{ \omega(\sqrt{n}) }[/math] far away from the starting point after [math]\displaystyle{ n }[/math] steps is bounded by [math]\displaystyle{ o(1) }[/math].
Generalization
Azuma's inequality can be generalized to a martingale with respect another sequence.
Azuma's Inequality (general version) - Let [math]\displaystyle{ Y_0,Y_1,\ldots }[/math] be a martingale with respect to the sequence [math]\displaystyle{ X_0,X_1,\ldots }[/math] such that, for all [math]\displaystyle{ k\ge 1 }[/math],
- [math]\displaystyle{ |Y_{k}-Y_{k-1}|\le c_k, }[/math]
- Then
- [math]\displaystyle{ \begin{align} \Pr\left[|Y_n-Y_0|\ge t\right]\le 2\exp\left(-\frac{t^2}{2\sum_{k=1}^nc_k^2}\right). \end{align} }[/math]
- Let [math]\displaystyle{ Y_0,Y_1,\ldots }[/math] be a martingale with respect to the sequence [math]\displaystyle{ X_0,X_1,\ldots }[/math] such that, for all [math]\displaystyle{ k\ge 1 }[/math],
The Proof of Azuma's Inueqality
We will only give the formal proof of the non-generalized version. The proof of the general version is almost identical, with the only difference that we work on random sequence [math]\displaystyle{ Y_i }[/math] conditioning on sequence [math]\displaystyle{ X_i }[/math].
The proof of Azuma's Inequality uses several ideas which are used in the proof of the Chernoff bounds. We first observe that the total deviation of the martingale sequence can be represented as the sum of deferences in every steps. Thus, as the Chernoff bounds, we are looking for a bound of the deviation of the sum of random variables. The strategy of the proof is almost the same as the proof of Chernoff bounds: we first apply Markov's inequality to the moment generating function, then we bound the moment generating function, and at last we optimize the parameter of the moment generating function. However, unlike the Chernoff bounds, the martingale differences are not independent any more. So we replace the use of the independence in the Chernoff bound by the martingale property. The proof is detailed as follows.
In order to bound the probability of [math]\displaystyle{ |X_n-X_0|\ge t }[/math], we first bound the upper tail [math]\displaystyle{ \Pr[X_n-X_0\ge t] }[/math]. The bound of the lower tail can be symmetrically proved with the [math]\displaystyle{ X_i }[/math] replaced by [math]\displaystyle{ -X_i }[/math].
Represent the deviation as the sum of differences
We define the martingale difference sequence: for [math]\displaystyle{ i\ge 1 }[/math], let
- [math]\displaystyle{ Y_i=X_i-X_{i-1}. }[/math]
It holds that
- [math]\displaystyle{ \begin{align} \mathbf{E}[Y_i\mid X_0,\ldots,X_{i-1}] &=\mathbf{E}[X_i-X_{i-1}\mid X_0,\ldots,X_{i-1}]\\ &=\mathbf{E}[X_i\mid X_0,\ldots,X_{i-1}]-\mathbf{E}[X_{i-1}\mid X_0,\ldots,X_{i-1}]\\ &=X_{i-1}-X_{i-1}\\ &=0. \end{align} }[/math]
The second to the last equation is due to the fact that [math]\displaystyle{ X_0,X_1,\ldots }[/math] is a martingale and the definition of conditional expectation.
Let [math]\displaystyle{ Z_n }[/math] be the accumulated differences
- [math]\displaystyle{ Z_n=\sum_{i=1}^n Y_i. }[/math]
The deviation [math]\displaystyle{ (X_n-X_0) }[/math] can be computed by the accumulated differences:
- [math]\displaystyle{ \begin{align} X_n-X_0 &=(X_1-X_{0})+(X_2-X_1)+\cdots+(X_n-X_{n-1})\\ &=\sum_{i=1}^n Y_i\\ &=Z_n. \end{align} }[/math]
We then only need to upper bound the probability of the event [math]\displaystyle{ Z_n\ge t }[/math].
Apply Markov's inequality to the moment generating function
The event [math]\displaystyle{ Z_n\ge t }[/math] is equivalent to that [math]\displaystyle{ e^{\lambda Z_n}\ge e^{\lambda t} }[/math] for [math]\displaystyle{ \lambda\gt 0 }[/math]. Apply Markov's inequality, we have
- [math]\displaystyle{ \begin{align} \Pr\left[Z_n\ge t\right] &=\Pr\left[e^{\lambda Z_n}\ge e^{\lambda t}\right]\\ &\le \frac{\mathbf{E}\left[e^{\lambda Z_n}\right]}{e^{\lambda t}}. \end{align} }[/math]
This is exactly the same as what we did to prove the Chernoff bound. Next, we need to bound the moment generating function [math]\displaystyle{ \mathbf{E}\left[e^{\lambda Z_n}\right] }[/math].
Bound the moment generating functions
The moment generating function
- [math]\displaystyle{ \begin{align} \mathbf{E}\left[e^{\lambda Z_n}\right] &=\mathbf{E}\left[\mathbf{E}\left[e^{\lambda Z_n}\mid X_0,\ldots,X_{n-1}\right]\right]\\ &=\mathbf{E}\left[\mathbf{E}\left[e^{\lambda (Z_{n-1}+Y_n)}\mid X_0,\ldots,X_{n-1}\right]\right]\\ &=\mathbf{E}\left[\mathbf{E}\left[e^{\lambda Z_{n-1}}\cdot e^{\lambda Y_n}\mid X_0,\ldots,X_{n-1}\right]\right]\\ &=\mathbf{E}\left[e^{\lambda Z_{n-1}}\cdot\mathbf{E}\left[e^{\lambda Y_n}\mid X_0,\ldots,X_{n-1}\right]\right] \end{align} }[/math]
The first and the last equations are due to the fundamental facts about conditional expectation which are proved by us in the first section.
We then upper bound the [math]\displaystyle{ \mathbf{E}\left[e^{\lambda Y_n}\mid X_0,\ldots,X_{n-1}\right] }[/math] by a constant. To do so, we need the following technical lemma which is proved by the convexity of [math]\displaystyle{ e^{\lambda Y_n} }[/math].
Lemma - Let [math]\displaystyle{ X }[/math] be a random variable such that [math]\displaystyle{ \mathbf{E}[X]=0 }[/math] and [math]\displaystyle{ |X|\le c }[/math]. Then for [math]\displaystyle{ \lambda\gt 0 }[/math],
- [math]\displaystyle{ \mathbf{E}[e^{\lambda X}]\le e^{\lambda^2c^2/2}. }[/math]
- Let [math]\displaystyle{ X }[/math] be a random variable such that [math]\displaystyle{ \mathbf{E}[X]=0 }[/math] and [math]\displaystyle{ |X|\le c }[/math]. Then for [math]\displaystyle{ \lambda\gt 0 }[/math],
Proof. Observe that for [math]\displaystyle{ \lambda\gt 0 }[/math], the function [math]\displaystyle{ e^{\lambda X} }[/math] of the variable [math]\displaystyle{ X }[/math] is convex in the interval [math]\displaystyle{ [-c,c] }[/math]. We draw a line between the two endpoints points [math]\displaystyle{ (-c, e^{-\lambda c}) }[/math] and [math]\displaystyle{ (c, e^{\lambda c}) }[/math]. The curve of [math]\displaystyle{ e^{\lambda X} }[/math] lies entirely below this line. Thus, - [math]\displaystyle{ \begin{align} e^{\lambda X} &\le \frac{c-X}{2c}e^{-\lambda c}+\frac{c+X}{2c}e^{\lambda c}\\ &=\frac{e^{\lambda c}+e^{-\lambda c}}{2}+\frac{X}{2c}(e^{\lambda c}-e^{-\lambda c}). \end{align} }[/math]
Since [math]\displaystyle{ \mathbf{E}[X]=0 }[/math], we have
- [math]\displaystyle{ \begin{align} \mathbf{E}[e^{\lambda X}] &\le \mathbf{E}[\frac{e^{\lambda c}+e^{-\lambda c}}{2}+\frac{X}{2c}(e^{\lambda c}-e^{-\lambda c})]\\ &=\frac{e^{\lambda c}+e^{-\lambda c}}{2}+\frac{e^{\lambda c}-e^{-\lambda c}}{2c}\mathbf{E}[X]\\ &=\frac{e^{\lambda c}+e^{-\lambda c}}{2}. \end{align} }[/math]
By expanding both sides as Taylor's series, it can be verified that [math]\displaystyle{ \frac{e^{\lambda c}+e^{-\lambda c}}{2}\le e^{\lambda^2c^2/2} }[/math].
- [math]\displaystyle{ \square }[/math]
Apply the above lemma to the random variable
- [math]\displaystyle{ (Y_n \mid X_0,\ldots,X_{n-1}) }[/math]
We have already shown that its expectation [math]\displaystyle{ \mathbf{E}[(Y_n \mid X_0,\ldots,X_{n-1})]=0, }[/math] and by the bounded difference condition of Azuma's inequality, we have [math]\displaystyle{ |Y_n|=|(X_n-X_{n-1})|\le c_n. }[/math] Thus, due to the above lemma, it holds that
- [math]\displaystyle{ \mathbf{E}[e^{\lambda Y_n}\mid X_0,\ldots,X_{n-1}]\le e^{\lambda^2c_n^2/2}. }[/math]
Back to our analysis of the expectation [math]\displaystyle{ \mathbf{E}\left[e^{\lambda Z_n}\right] }[/math], we have
- [math]\displaystyle{ \begin{align} \mathbf{E}\left[e^{\lambda Z_n}\right] &=\mathbf{E}\left[e^{\lambda Z_{n-1}}\cdot\mathbf{E}\left[e^{\lambda Y_n}\mid X_0,\ldots,X_{n-1}\right]\right]\\ &\le \mathbf{E}\left[e^{\lambda Z_{n-1}}\cdot e^{\lambda^2c_n^2/2}\right]\\ &= e^{\lambda^2c_n^2/2}\cdot\mathbf{E}\left[e^{\lambda Z_{n-1}}\right] . \end{align} }[/math]
Apply the same analysis to [math]\displaystyle{ \mathbf{E}\left[e^{\lambda Z_{n-1}}\right] }[/math], we can solve the above recursion by
- [math]\displaystyle{ \begin{align} \mathbf{E}\left[e^{\lambda Z_n}\right] &\le \prod_{k=1}^n e^{\lambda^2c_k^2/2}\\ &= \exp\left(\lambda^2\sum_{k=1}^n c_k^2/2\right). \end{align} }[/math]
Go back to the Markov's inequality,
- [math]\displaystyle{ \begin{align} \Pr\left[Z_n\ge t\right] &\le \frac{\mathbf{E}\left[e^{\lambda Z_n}\right]}{e^{\lambda t}}\\ &\le \exp\left(\lambda^2\sum_{k=1}^n c_k^2/2-\lambda t\right). \end{align} }[/math]
We then only need to choose a proper [math]\displaystyle{ \lambda\gt 0 }[/math].
Optimization
By choosing [math]\displaystyle{ \lambda=\frac{t}{\sum_{k=1}^n c_k^2} }[/math], we have that
- [math]\displaystyle{ \exp\left(\lambda^2\sum_{k=1}^n c_k^2/2-\lambda t\right)=\exp\left(-\frac{t^2}{2\sum_{k=1}^n c_k^2}\right). }[/math]
Thus, the probability
- [math]\displaystyle{ \begin{align} \Pr\left[X_n-X_0\ge t\right] &=\Pr\left[Z_n\ge t\right]\\ &\le \exp\left(\lambda^2\sum_{k=1}^n c_k^2/2-\lambda t\right)\\ &= \exp\left(-\frac{t^2}{2\sum_{k=1}^n c_k^2}\right). \end{align} }[/math]
The upper tail of Azuma's inequality is proved. By replacing [math]\displaystyle{ X_i }[/math] by [math]\displaystyle{ -X_i }[/math], the lower tail can be treated just as the upper tail. Applying the union bound, Azuma's inequality is proved.