组合数学 (Fall 2024)/Problem Set 2

Problem 1

Count the number of lattice paths from $(0,0)$ to $(n,n)$ with steps up and to the right, when two paths are considered equal if one can be moved on top of the other by a rotation or reflection. For example:

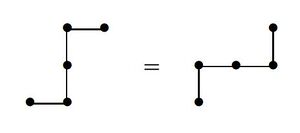
Hint: Represent a path as a sequence of $0$s and $1$s and determine the group that acts on these sequences.

Problem 2

Suppose we are given $m$ $n$-sets whose elements are colored with two colors. Two colorings are equal if they arise from each other by a permutation of the $m$ sets followed by permutations of the individual sets. Determine the number of different colorings using Pólya's enumeration formula. (The answer should be easily verifiable through combinatorial arguments if you get it right!)

Problem 3

Prove the following claims related to Cayley's formula:

• The number of rooted labelled forests with $n$ vertices is given by $(n+1{)}^{n-1}$.

• The number of unrooted labelled forests with $n$ vertices and $k$ connected components such that $1,\dots ,k$ belong to distinct components is given by $k{n}^{n-k-1}$.

• The number of unrooted labelled trees with $n$ vertices of degrees $d_1,d_2,\dots ,d_n$ respectively is given by $(\genfrac{}{}{0ex}{}{n-2}{d_1-1,d_2-1,\dots ,d_n-1})=\frac{(n-2)!}{(d_1-1)!(d_2-1)!\cdots (d_n-1)!}$.

Problem 4

There are $n$ parking spaces $1,2,...,n$ available for $n$ drivers. Each driver has a favorite space, driver $i$ space $f(i)$, $1\le f(i)\le n$. The drivers arrive one by one. When driver $i$ arrives he tries to park his car in space $f(i)$. If it is taken he moves down the line to take the first free space greater than $f(i)$, if any. Example: $n=4,f=3221$; then driver $1\to 3,2\to 2,3\to 4,4\to 1$, but for $f=2332$ we have $1\to 2,2\to 3,3\to 4,2\to ?$ Let $p(n)$ be the number of sequences $f$ that allow each driver to park his car; $f$ is then called a parking sequence. Prove:

• $f$ is a parking sequence if and only if $\mathrm{\#}\{i:f(i)\le k\}\ge k$.
• $p(n)=(n+1{)}^{n-1}$. This looks like the number of rooted labelled forests with $n$ vertices. Can you find a bijection?

Problem 5

Let's dive into the world of (one-way) communication complexity. Alice has an input $\mathbf{x}\in \{0,1{\}}^a$ , Bob has an input $\mathbf{y}\in \{0,1{\}}^b$ , and the goal is to compute a Boolean function $f:\{0,1{\}}^a\times \{0,1{\}}^b\to \{0,1\}$ of the joint input $(\mathbf{x},\mathbf{y})$. The players communicate as follows: Alice sends a message $\mathbf{z}$ to Bob as a function of $\mathbf{x}$ only (she doesn’t know Bob's input $\mathbf{y}$), and Bob has to decide the function $f$ knowing only $\mathbf{z}$ and $\mathbf{y}$ (he doesn't know Alice's input $x$). The one-way communication complexity of $f$ is the smallest number of bits communicated (in the worst case over $(\mathbf{x},\mathbf{y})$) of any protocol that computes $f$.

We consider the (one-way) communication complexity of a problem called $\mathrm{I}\mathrm{N}\mathrm{D}\mathrm{E}\mathrm{X}$. In an instance of $\mathrm{I}\mathrm{N}\mathrm{D}\mathrm{E}\mathrm{X}$, Alice gets an $n$-bit string $\mathbf{x}\in \{0,1{\}}^n$ and Bob gets an integer $i\in \{1,2,...,n\}$, encoded in binary using $\approx {\log }_{2}n$ bits. The goal is simply to compute $x_i$, the $i$th bit of Alice's input.

• Show that the deterministic (one-way) communication complexity of $\mathrm{I}\mathrm{N}\mathrm{D}\mathrm{E}\mathrm{X}$ is $\mathrm{\Omega }(n)$. (For a deterministic communication protocol, the protocol is considered to solve $\mathrm{I}\mathrm{N}\mathrm{D}\mathrm{E}\mathrm{X}$ if Bob always outputs the correct answer in the worst case over $(\mathbf{x},\mathbf{y})$ );

• Show that the randomized (one-way) communication complexity of $\mathrm{I}\mathrm{N}\mathrm{D}\mathrm{E}\mathrm{X}$ is $\mathrm{\Omega }(n)$. (In a randomized communication protocol, Alice and Bob have access to public random bits: a deity writes an infinite sequence of perfectly random bits on a blackboard visible to both Alice and Bob. Alice and Bob can freely use as many of these random bits as they want — it doesn't contribute to the communication cost of the protocol. The protocol is considered to solve $\mathrm{I}\mathrm{N}\mathrm{D}\mathrm{E}\mathrm{X}$ if Bob outputs the correct answer with probability at least $2/3$ in the worst case over $(\mathbf{x},\mathbf{y})$ ).

(Hint: We need to formalize the intuition that Bob typically (over $\mathbf{x}$) doesn't learn very much about $\mathbf{x}$, and hence typically (over $i$) doesn't know what $x_i$ is. Try some counting arguments.)