Combinatorics (Fall 2010)/Partitions, sieve methods

Principle of Inclusion-Exclusion

Let [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] be two finite sets. The cardinality of their union is

[math]\displaystyle{ |A\cup B|=|A|+|B|-{\color{Blue}|A\cap B|} }[/math].

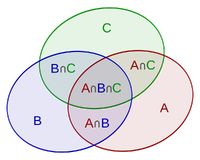
For three sets [math]\displaystyle{ A }[/math], [math]\displaystyle{ B }[/math], and [math]\displaystyle{ C }[/math], the cardinality of the union of these three sets is computed as

[math]\displaystyle{ |A\cup B\cup C|=|A|+|B|+|C|-{\color{Blue}|A\cap B|}-{\color{Blue}|A\cap C|}-{\color{Blue}|B\cap C|}+{\color{Red}|A\cap B\cap C|} }[/math].

This is illustrated by the following figure.

Generally, the Principle of Inclusion-Exclusion states the rule for computing the union of [math]\displaystyle{ n }[/math] finite sets [math]\displaystyle{ A_1,A_2,\ldots,A_n }[/math], such that

[math]\displaystyle{ \begin{align} \left|\bigcup_{i=1}^nA_i\right| &= \sum_{I\subseteq\{1,\ldots,n\}}(-1)^{|I|-1}\left|\bigcap_{i\in I}A_i\right|. \end{align} }[/math]

---

In combinatorial enumeration, the Principle of Inclusion-Exclusion is usually applied in its complement form.

Let [math]\displaystyle{ A_1,A_2,\ldots,A_n\subseteq U }[/math] be subsets of some finite set [math]\displaystyle{ U }[/math]. Here [math]\displaystyle{ U }[/math] is some universe of combinatorial objects, whose cardinality is easy to calculate (e.g. all strings, tuples, permutations), and each [math]\displaystyle{ A_i }[/math] contains the objects with some specific property (e.g. a "pattern") which we want to avoid. The problem is to count the number of objects without any of the [math]\displaystyle{ n }[/math] properties. We write [math]\displaystyle{ \bar{A_i}=U-A }[/math]. The number of objects without any of the properties [math]\displaystyle{ A_1,A_2,\ldots,A_n }[/math] is

[math]\displaystyle{ \begin{align} \left|\bar{A_1}\cap\bar{A_2}\cap\cdots\cap\bar{A_n}\right|=\left|U-\bigcup_{i=1}^nA_i\right| &= |U|-\sum_{I\subseteq\{1,\ldots,n\}}(-1)^{|I|}\left|\bigcap_{i\in I}A_i\right|. \end{align} }[/math]

For an [math]\displaystyle{ I\subseteq\{1,2,\ldots,n\} }[/math], we denote

[math]\displaystyle{ A_I=\bigcap_{i\in I}A_i }[/math]

with the convention that [math]\displaystyle{ A_\emptyset=U }[/math]. The above equation is stated as:

Principle of Inclusion-Exclusion

Let [math]\displaystyle{ A_1,A_2,\ldots,A_n }[/math] be a family of subsets of [math]\displaystyle{ U }[/math]. Then the number of elements of [math]\displaystyle{ U }[/math] which lie in none of the subsets [math]\displaystyle{ A_i }[/math] is [math]\displaystyle{ \sum_{I\subseteq\{1,\ldots, n\}}(-1)^{|I|}|A_I| }[/math].

Let [math]\displaystyle{ S_k=\sum_{|I|=k}|A_I|\, }[/math]. Conventionally, [math]\displaystyle{ S_0=|A_\emptyset|=|U| }[/math]. The principle of inclusion-exclusion can be expressed as

[math]\displaystyle{ S_0-S_1+S_2+\cdots+(-1)^nS_n. }[/math]

Surjections

In the twelvefold way, we discuss the counting problems incurred by the mappings [math]\displaystyle{ f:N\rightarrow M }[/math]. The basic case is that elements from both [math]\displaystyle{ N }[/math] and [math]\displaystyle{ M }[/math] are distinguishable. In this case, it is easy to count the number of arbitrary mappings (which is [math]\displaystyle{ m^n }[/math]) and the number of injective (one-to-one) mappings (which is [math]\displaystyle{ (m)_n }[/math]), but the number of surjective is difficult. Here we apply the principle of inclusion-exclusion to count the number of surjective (onto) mappings.

Theorem

The number of surjective mappings from an [math]\displaystyle{ n }[/math]-set to an [math]\displaystyle{ m }[/math]-set is given by [math]\displaystyle{ \sum_{k=1}^m(-1)^{m-k}{m\choose k}k^n }[/math].

Proof. Let [math]\displaystyle{ U=\{f:[n]\rightarrow[m]\} }[/math] be the set of mappings from [math]\displaystyle{ [n] }[/math] to [math]\displaystyle{ [m] }[/math]. Then [math]\displaystyle{ |U|=m^n }[/math]. For [math]\displaystyle{ i\in[m] }[/math], let [math]\displaystyle{ A_i }[/math] be the set of mappings [math]\displaystyle{ f:[n]\rightarrow[m] }[/math] that none of [math]\displaystyle{ j\in[n] }[/math] is mapped to [math]\displaystyle{ i }[/math], i.e. [math]\displaystyle{ A_i=\{f:[n]\rightarrow[m]\setminus\{i\}\} }[/math], thus [math]\displaystyle{ |A_i|=(m-1)^n }[/math]. More generally, for [math]\displaystyle{ I\subseteq [m] }[/math], [math]\displaystyle{ A_I=\bigcap_{i\in I}A_i }[/math] contains the mappings [math]\displaystyle{ f:[n]\rightarrow[m]\setminus I }[/math]. And [math]\displaystyle{ |A_I|=(m-|I|)^n\, }[/math]. A mapping [math]\displaystyle{ f:[n]\rightarrow[m] }[/math] is surjective if [math]\displaystyle{ f }[/math] lies in none of [math]\displaystyle{ A_i }[/math]. By the principle of inclusion-exclusion, the number of surjective [math]\displaystyle{ f:[n]\rightarrow[m] }[/math] is [math]\displaystyle{ \sum_{\subseteq[m]}(-1)^{|I|}\left|A_I\right|=\sum_{I\subseteq[m]}(-1)^{|I|}(m-|I|)^n=\sum_{j=0}^m(-1)^j{m\choose j}(m-j)^n }[/math]. Let [math]\displaystyle{ k=m-j }[/math]. The theorem is proved. [math]\displaystyle{ \square }[/math]

Recall that, in the twelvefold way, we establish a relation between surjections and partitions.

• Surjection to ordered partition:

For a surjective [math]\displaystyle{ f:[n]\rightarrow[m] }[/math], [math]\displaystyle{ (f^{-1}(0),f^{-1}(1),\ldots,f^{-1}(m-1)) }[/math] is an ordered partition of [math]\displaystyle{ [n] }[/math].

• Ordered partition to surjection:

For an ordered [math]\displaystyle{ m }[/math]-partition [math]\displaystyle{ (B_0,B_1,\ldots, B_{m-1}) }[/math] of [math]\displaystyle{ [n] }[/math], we can define a function [math]\displaystyle{ f:[n]\rightarrow[m] }[/math] by letting [math]\displaystyle{ f(i)=j }[/math] if and only if [math]\displaystyle{ i\in B_j }[/math]. [math]\displaystyle{ f }[/math] is surjective since as a partition, none of [math]\displaystyle{ B_i }[/math] is empty.

Therefore, we have a one-to-one correspondence between surjective mappings from an [math]\displaystyle{ n }[/math]-set to an [math]\displaystyle{ m }[/math]-set and the ordered [math]\displaystyle{ m }[/math]-partitions of an [math]\displaystyle{ n }[/math]-set.

The Stirling number of the second kind [math]\displaystyle{ S(n,m) }[/math] is the number of [math]\displaystyle{ m }[/math]-partitions of an [math]\displaystyle{ n }[/math]-set. There are [math]\displaystyle{ m! }[/math] ways to order an [math]\displaystyle{ m }[/math]-partition, thus the number of surjective mappings [math]\displaystyle{ f:[n]\rightarrow[m] }[/math] is [math]\displaystyle{ m! S(n,m) }[/math]. Combining with what we have proved for surjections, we give the following result for the Stirling number of the second kind.

Proposition

[math]\displaystyle{ S(n,m)=\frac{1}{m!}\sum_{k=1}^m(-1)^{m-k}{m\choose k}k^n }[/math].