高级算法 (Fall 2019)/Concentration of measure

Chernoff Bound

Suppose that we have a fair coin. If we toss it once, then the outcome is completely unpredictable. But if we toss it, say for 1000 times, then the number of HEADs is very likely to be around 500. This phenomenon, as illustrated in the following figure, is called the concentration of measure. The Chernoff bound is an inequality that characterizes the concentration phenomenon for the sum of independent trials.

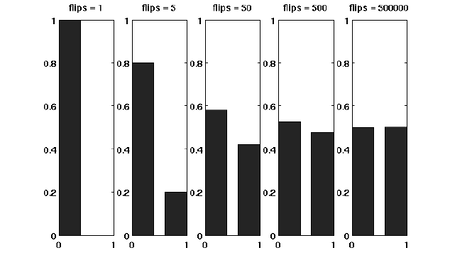
Before formally stating the Chernoff bound, let's introduce the moment generating function.

Moment generating functions

The more we know about the moments of a random variable $X$, the more information we would have about $X$. There is a so-called moment generating function, which "packs" all the information about the moments of $X$ into one function.

Definition

The moment generating function of a random variable $X$ is defined as $\mathbf{E}\left[{\mathrm{e}}^{\lambda X}\right]$ where $\lambda$ is the parameter of the function.

By Taylor's expansion and the linearity of expectations,

$\begin{array}{rl}\mathbf{E}\left[{\mathrm{e}}^{\lambda X}\right]& =\mathbf{E}\left[\sum _{k=0}^{\mathrm{\infty }}\frac{{\lambda }^k}{k!}{X}^k\right]\\ & =\sum _{k=0}^{\mathrm{\infty }}\frac{{\lambda }^k}{k!}\mathbf{E}\left[X^k\right]\end{array}$

The moment generating function $\mathbf{E}\left[{\mathrm{e}}^{\lambda X}\right]$ is a function of $\lambda$.

The Chernoff bound

The Chernoff bounds are exponentially sharp tail inequalities for the sum of independent trials. The bounds are obtained by applying Markov's inequality to the moment generating function of the sum of independent trials, with some appropriate choice of the parameter $\lambda$.

Chernoff bound (the upper tail)

Let $X=\sum _{i=1}^n{X}_i$, where $X_1,X_2,\dots ,X_n$ are independent Poisson trials. Let $\mu =\mathbf{E}[X]$. Then for any $\delta >0$, $Pr[X\ge (1+\delta )\mu ]\le {\left(\frac{e^{\delta }}{(1+\delta {)}^{(1+\delta )}}\right)}^{\mu }.$

Proof. For any $\lambda >0$, $X\ge (1+\delta )\mu$ is equivalent to that $e^{\lambda X}\ge e^{\lambda (1+\delta )\mu }$, thus $\begin{array}{rl}Pr[X\ge (1+\delta )\mu ]& =Pr[e^{\lambda X}\ge e^{\lambda (1+\delta )\mu }]\\ & \le \frac{\mathbf{E}\left[e^{\lambda X}\right]}{e^{\lambda (1+\delta )\mu }},\end{array}$ where the last step follows by Markov's inequality. Computing the moment generating function $\mathbf{E}[e^{\lambda X}]$: $\begin{array}{rl}\mathbf{E}\left[e^{\lambda X}\right]& =\mathbf{E}\left[e^{\lambda \sum _{i=1}^n{X}_i}\right]\\ & =\mathbf{E}\left[\prod _{i=1}^n{e}^{\lambda X_i}\right]\\ & =\prod _{i=1}^n\mathbf{E}\left[e^{\lambda X_i}\right].& (\text{for independent random variables})\end{array}$ Let $p_i=Pr[X_i=1]$ for $i=1,2,\dots ,n$. Then, $\mu =\mathbf{E}[X]=\mathbf{E}\left[\sum _{i=1}^n{X}_i\right]=\sum _{i=1}^n\mathbf{E}[X_i]=\sum _{i=1}^n{p}_i$. We bound the moment generating function for each individual $X_i$ as follows. $\begin{array}{rl}\mathbf{E}\left[e^{\lambda X_i}\right]& =p_i\cdot e^{\lambda \cdot 1}+(1-p_i)\cdot e^{\lambda \cdot 0}\\ & =1+p_i(e^{\lambda }-1)\\ & \le e^{p_i(e^{\lambda }-1)},\end{array}$ where in the last step we apply the Taylor's expansion so that $e^y\ge 1+y$ where $y=p_i(e^{\lambda }-1)\ge 0$. (By doing this, we can transform the product to the sum of $p_i$, which is $\mu$.) Therefore, $\begin{array}{rl}\mathbf{E}\left[e^{\lambda X}\right]& =\prod _{i=1}^n\mathbf{E}\left[e^{\lambda X_i}\right]\\ & \le \prod _{i=1}^n{e}^{p_i(e^{\lambda }-1)}\\ & =\exp (\sum _{i=1}^n{p}_i(e^{\lambda }-1))\\ & =e^{(e^{\lambda }-1)\mu }.\end{array}$ Thus, we have shown that for any $\lambda >0$, $\begin{array}{rl}Pr[X\ge (1+\delta )\mu ]& \le \frac{\mathbf{E}\left[e^{\lambda X}\right]}{e^{\lambda (1+\delta )\mu }}\\ & \le \frac{e^{(e^{\lambda }-1)\mu }}{e^{\lambda (1+\delta )\mu }}\\ & ={\left(\frac{e^{(e^{\lambda }-1)}}{e^{\lambda (1+\delta )}}\right)}^{\mu }\end{array}$. For any $\delta >0$, we can let $\lambda =\ln (1+\delta )>0$ to get $Pr[X\ge (1+\delta )\mu ]\le {\left(\frac{e^{\delta }}{(1+\delta {)}^{(1+\delta )}}\right)}^{\mu }.$ $◻$

The idea of the proof is actually quite clear: we apply Markov's inequality to $e^{\lambda X}$ and for the rest, we just estimate the moment generating function $\mathbf{E}[e^{\lambda X}]$. To make the bound as tight as possible, we minimized the $\frac{e^{(e^{\lambda }-1)}}{e^{\lambda (1+\delta )}}$ by setting $\lambda =\ln (1+\delta )$, which can be justified by taking derivatives of $\frac{e^{(e^{\lambda }-1)}}{e^{\lambda (1+\delta )}}$.

---

We then proceed to the lower tail, the probability that the random variable deviates below the mean value:

Chernoff bound (the lower tail)

Let $X=\sum _{i=1}^n{X}_i$, where $X_1,X_2,\dots ,X_n$ are independent Poisson trials. Let $\mu =\mathbf{E}[X]$. Then for any $0<\delta <1$, $Pr[X\le (1-\delta )\mu ]\le {\left(\frac{e^{-\delta }}{(1-\delta {)}^{(1-\delta )}}\right)}^{\mu }.$

Proof. For any $\lambda <0$, by the same analysis as in the upper tail version, $\begin{array}{rl}Pr[X\le (1-\delta )\mu ]& =Pr[e^{\lambda X}\ge e^{\lambda (1-\delta )\mu }]\\ & \le \frac{\mathbf{E}\left[e^{\lambda X}\right]}{e^{\lambda (1-\delta )\mu }}\\ & \le {\left(\frac{e^{(e^{\lambda }-1)}}{e^{\lambda (1-\delta )}}\right)}^{\mu }.\end{array}$ For any $0<\delta <1$, we can let $\lambda =\ln (1-\delta )<0$ to get $Pr[X\ge (1-\delta )\mu ]\le {\left(\frac{e^{-\delta }}{(1-\delta {)}^{(1-\delta )}}\right)}^{\mu }.$ $◻$

Useful forms of the Chernoff bounds

Some useful special forms of the bounds can be derived directly from the above general forms of the bounds. We now know better why we say that the bounds are exponentially sharp.

Useful forms of the Chernoff bound

Let $X=\sum _{i=1}^n{X}_i$, where $X_1,X_2,\dots ,X_n$ are independent Poisson trials. Let $\mu =\mathbf{E}[X]$. Then 1. for $0<\delta \le 1$, $Pr[X\ge (1+\delta )\mu ]<\exp (-\frac{\mu {\delta }^2}{3});$ $Pr[X\le (1-\delta )\mu ]<\exp (-\frac{\mu {\delta }^2}{2});$ 2. for $t\ge 2e\mu$, $Pr[X\ge t]\le 2^{-t}.$

Proof. To obtain the bounds in (1), we need to show that for $0<\delta <1$, $\frac{e^{\delta }}{(1+\delta {)}^{(1+\delta )}}\le e^{-{\delta }^2/3}$ and $\frac{e^{-\delta }}{(1-\delta {)}^{(1-\delta )}}\le e^{-{\delta }^2/2}$. We can verify both inequalities by standard analysis techniques. To obtain the bound in (2), let $t=(1+\delta )\mu$. Then $\delta =t/\mu -1\ge 2e-1$. Hence, $\begin{array}{rl}Pr[X\ge (1+\delta )\mu ]& \le {\left(\frac{e^{\delta }}{(1+\delta {)}^{(1+\delta )}}\right)}^{\mu }\\ & \le {\left(\frac{e}{1+\delta }\right)}^{(1+\delta )\mu }\\ & \le {\left(\frac{e}{2e}\right)}^t\\ & \le 2^{-t}\end{array}$ $◻$

Applications to balls-into-bins

Throwing $m$ balls uniformly and independently to $n$ bins, what is the maximum load of all bins with high probability? In the last class, we gave an analysis of this problem by using a counting argument.

Now we give a more "advanced" analysis by using Chernoff bounds.

For any $i\in [n]$ and $j\in [m]$, let $X_{ij}$ be the indicator variable for the event that ball $j$ is thrown to bin $i$. Obviously

$\mathbf{E}[X_{ij}]=Pr[\text{ball }j\text{ is thrown to bin }i]=\frac{1}{n}$

Let $Y_i=\sum _{j\in [m]}{X}_{ij}$ be the load of bin $i$.

Then the expected load of bin $i$ is

$(\ast )\mu =\mathbf{E}[Y_i]=\mathbf{E}\left[\sum _{j\in [m]}{X}_{ij}\right]=\sum _{j\in [m]}\mathbf{E}[X_{ij}]=m/n.$

For the case $m=n$, it holds that $\mu =1$

Note that $Y_i$ is a sum of $m$ mutually independent indicator variable. Applying Chernoff bound, for any particular bin $i\in [n]$,

$Pr[Y_i>(1+\delta )\mu ]\le {\left(\frac{e^{\delta }}{(1+\delta {)}^{1+\delta }}\right)}^{\mu }.$

The $m=n$ case

When $m=n$, $\mu =1$. Write $c=1+\delta$. The above bound can be written as

$Pr[Y_i>c]\le \frac{e^{c-1}}{c^c}.$

Let $c=\frac{e\ln n}{\ln \ln n}$, we evaluate $\frac{e^{c-1}}{c^c}$ by taking logarithm to its reciprocal.

$\begin{array}{rl}\ln \left(\frac{c^c}{e^{c-1}}\right)& =c\ln c-c+1\\ & =c(\ln c-1)+1\\ & =\frac{e\ln n}{\ln \ln n}(\ln \ln n-\ln \ln \ln n)+1\\ & \ge \frac{e\ln n}{\ln \ln n}\cdot \frac{2}{e}\ln \ln n+1\\ & \ge 2\ln n.\end{array}$

Thus,

$Pr[Y_i>\frac{e\ln n}{\ln \ln n}]\le \frac{1}{n^2}.$

Applying the union bound, the probability that there exists a bin with load $>12\ln n$ is

$n\cdot Pr[Y_1>\frac{e\ln n}{\ln \ln n}]\le \frac{1}{n}$.

Therefore, for $m=n$, with high probability, the maximum load is $O\left(\frac{e\ln n}{\ln \ln n}\right)$.

The $m>\ln n$ case

When $m\ge n\ln n$, then according to $(\ast )$, $\mu =\frac{m}{n}\ge \ln n$

We can apply an easier form of the Chernoff bounds,

$Pr[Y_i\ge 2e\mu ]\le 2^{-2e\mu }\le 2^{-2e\ln n}<\frac{1}{n^2}.$

By the union bound, the probability that there exists a bin with load $\ge 2e\frac{m}{n}$ is,

$n\cdot Pr[Y_1>2e\frac{m}{n}]=n\cdot Pr[Y_1>2e\mu ]\le \frac{1}{n}$.

Therefore, for $m\ge n\ln n$, with high probability, the maximum load is $O\left(\frac{m}{n}\right)$.

Martingales

"Martingale" originally refers to a betting strategy in which the gambler doubles his bet after every loss. Assuming unlimited wealth, this strategy is guaranteed to eventually have a positive net profit. For example, starting from an initial stake 1, after $n$ losses, if the $(n+1)$th bet wins, then it gives a net profit of

$2^n-\sum _{i=1}^n{2}^{i-1}=1,$

which is a positive number.

However, the assumption of unlimited wealth is unrealistic. For limited wealth, with geometrically increasing bet, it is very likely to end up bankrupt. You should never try this strategy in real life.

Suppose that the gambler is allowed to use any strategy. His stake on the next beting is decided based on the results of all the bettings so far. This gives us a highly dependent sequence of random variables $X_0,X_1,\dots ,$, where $X_0$ is his initial capital, and $X_i$ represents his capital after the $i$th betting. Up to different betting strategies, $X_i$ can be arbitrarily dependent on $X_0,\dots ,X_{i-1}$. However, as long as the game is fair, namely, winning and losing with equal chances, conditioning on the past variables $X_0,\dots ,X_{i-1}$, we will expect no change in the value of the present variable $X_i$ on average. Random variables satisfying this property is called a martingale sequence.

Definition (martingale)

A sequence of random variables $X_0,X_1,\dots$ is a martingale if for all $i>0$, $\begin{array}{r}\mathbf{E}[X_i\mid X_0,\dots ,X_{i-1}]=X_{i-1}.\end{array}$