Randomized Algorithms (Spring 2010)/Balls and bins

Probability Basics

Independent events

We are all familiar with the concept of independent events:

Definition (Independent events): Two events [math]\displaystyle{ \mathcal{E}_1 }[/math] and [math]\displaystyle{ \mathcal{E}_2 }[/math] are independent if and only if [math]\displaystyle{ \begin{align} \Pr\left[\mathcal{E}_1 \wedge \mathcal{E}_2\right] &= \Pr[\mathcal{E}_1]\cdot\Pr[\mathcal{E}_2]. \end{align} }[/math]

This definition can be generalized to more events:

Definition (Independent events): Events [math]\displaystyle{ \mathcal{E}_1, \mathcal{E}_2, \ldots, \mathcal{E}_n }[/math] are mutually independent if and only if, for any subset [math]\displaystyle{ I\subseteq\{1,2,\ldots,n\} }[/math], [math]\displaystyle{ \begin{align} \Pr\left[\bigwedge_{i\in I}\mathcal{E}_i\right] &= \prod_{i\in I}\Pr[\mathcal{E}_i]. \end{align} }[/math]

Note that in probability theory, the word "mutually independent" is not equivalent with "pair-wise independent", which we will learn in the future.

The union bound

We are familiar with the principle of inclusion-exclusion for finite sets.

Principle of Inclusion-Exclusion: Let [math]\displaystyle{ S_1, S_2, \ldots, S_n }[/math] be [math]\displaystyle{ n }[/math] finite sets. Then [math]\displaystyle{ \begin{align} \left|\bigcup_{1\le i\le n}S_i\right| &= \sum_{i=1}^n|S_i| -\sum_{i\lt j}|S_i\cap S_j| +\sum_{i\lt j\lt k}|S_i\cap S_j\cap S_k|\\ & \quad -\cdots +(-1)^{\ell-1}\sum_{i_1\lt i_2\lt \cdots\lt i_\ell}\left|\bigcap_{r=1}^\ell S_{i_r}\right| +\cdots +(-1)^{n-1} \left|\bigcap_{i=1}^n S_i\right|. \end{align} }[/math]

The principle can be generalized to probability events.

Principle of Inclusion-Exclusion: Let [math]\displaystyle{ \mathcal{E}_1, \mathcal{E}_2, \ldots, \mathcal{E}_n }[/math] be [math]\displaystyle{ n }[/math] events. Then [math]\displaystyle{ \begin{align} \Pr\left[\bigvee_{1\le i\le n}\mathcal{E}_i\right] &= \sum_{i=1}^n\Pr[\mathcal{E}_i] -\sum_{i\lt j}\Pr[\mathcal{E}_i\wedge \mathcal{E}_j] +\sum_{i\lt j\lt k}\Pr[\mathcal{E}_i\wedge \mathcal{E}_j\wedge \mathcal{E}_k]\\ & \quad -\cdots +(-1)^{\ell-1}\sum_{i_1\lt i_2\lt \cdots\lt i_\ell}\Pr\left[\bigwedge_{r=1}^\ell \mathcal{E}_{i_r}\right] +\cdots +(-1)^{n-1}\Pr\left[\bigwedge_{i=1}^n \mathcal{E}_{i}\right]. \end{align} }[/math]

The proof of the principle is due to measure theory, and is omitted here. The following inequality is implied (nontrivially) by the principle of inclusion-exclusion:

Theorem (the union bound): Let [math]\displaystyle{ \mathcal{E}_1, \mathcal{E}_2, \ldots, \mathcal{E}_n }[/math] be [math]\displaystyle{ n }[/math] events. Then [math]\displaystyle{ \begin{align} \Pr\left[\bigvee_{1\le i\le n}\mathcal{E}_i\right] &\le \sum_{i=1}^n\Pr[\mathcal{E}_i]. \end{align} }[/math]

The name of this inequality is Boole's inequality. It is usually referred by its nickname "the union bound". The bound holds for arbitrary events, even if they are dependent. Due to this generality, the union bound is one of the most useful probability inequalities for randomized algorithm analysis.

Linearity of expectation

Let [math]\displaystyle{ X }[/math] be a discrete random variable. The expectation of [math]\displaystyle{ X }[/math] is defined as follows.

Definition (Expectation): The expectation of a discrete random variable [math]\displaystyle{ X }[/math], denoted by [math]\displaystyle{ \mathbb{E}[X] }[/math], is given by [math]\displaystyle{ \begin{align} \mathbb{E}[X] &= \sum_{x}x\Pr[X=x], \end{align} }[/math] where the summation is over all values [math]\displaystyle{ x }[/math] in the range of [math]\displaystyle{ X }[/math].

A key property of expectations is the linearity.

Theorem (Linearity of Expectations): For any discrete random variables [math]\displaystyle{ X_1, X_2, \ldots, X_n }[/math], and any real constants [math]\displaystyle{ a_1, a_2, \ldots, a_n }[/math], [math]\displaystyle{ \begin{align} \mathbb{E}\left[\sum_{i=1}^n a_iX_i\right] &= \sum_{i=1}^n a_i\cdot\mathbb{E}[X_i]. \end{align} }[/math]

Proof: By the definition of the expectations, it is easy to verify that (try to prove by yourself): for any discrete random variables [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math], and any real constant [math]\displaystyle{ c }[/math],

• [math]\displaystyle{ \mathbb{E}[X+Y]=\mathbb{E}[X]+\mathbb{E}[Y] }[/math];
• [math]\displaystyle{ \mathbb{E}[cX]=c\mathbb{E}[X] }[/math].

The theorem follows by induction. [math]\displaystyle{ \square }[/math]

---

An extremely powerful feature of the linearity of expectations is that it does not require the random variables to be independent, thus can be applied to any set of random variables. For example:

[math]\displaystyle{ \mathbb{E}\left[\alpha X+\beta X^2+\gamma X^3\right] = \alpha\cdot\mathbb{E}[X]+\beta\cdot\mathbb{E}\left[X^2\right]+\gamma\cdot\mathbb{E}\left[X^3\right]. }[/math]

However, do not overly-generalize this power!

• For an arbitrary function [math]\displaystyle{ f }[/math] (not necessarily linear), the equation [math]\displaystyle{ \mathbb{E}[f(X)]=f(\mathbb{E}[X]) }[/math] does not hold generally.
• For higher-order moment such as variance, the equation [math]\displaystyle{ var(X+Y)=var(X)+var(Y) }[/math] does not hold without further assumption of the independence of [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math].

Balls-into-bins model

Imagine that [math]\displaystyle{ m }[/math] balls are thrown into [math]\displaystyle{ n }[/math] bins, in such a way that each ball is thrown into a bin which is uniformly and independently chosen from all [math]\displaystyle{ n }[/math] bins.

There are several interesting questions we could ask about this random process. For example:

• the probability that there is no bin with more than one balls (the birthday problem)
• the expected number of balls in each bin (occupancy problem)
• the maximum load of all bins with high probability (occupancy problem)
• the probability that there is no empty bin (coupon collector problem)

The birthday paradox

There are [math]\displaystyle{ m }[/math] students in the class. Assume that for each student, his/her birthday is uniformly and independently distributed over the 365 days in a years. We wonder what the probability that no two students share a birthday.

Due to the pigeonhole principle, it is obvious that for [math]\displaystyle{ m\gt 365 }[/math], there must be two students with the same birthday. Surprisingly, for any [math]\displaystyle{ m\gt 57 }[/math] this event occurs with more than 99% probability. This is called the birthday paradox. Despite the name, the birthday paradox is not a real paradox.

We can model this problem as a balls-into-bins problem. [math]\displaystyle{ m }[/math] different balls (students) are uniformly and independently thrown into 365 bins (days). More generally, let [math]\displaystyle{ n }[/math] be the number of bins. We ask for the probability of the following event [math]\displaystyle{ \mathcal{E} }[/math]

[math]\displaystyle{ \mathcal{E} }[/math]: there is no bin with more than one balls (i.e. no two students share birthday).

We first analyze this by counting. There are totally [math]\displaystyle{ n^m }[/math] many ways of assigning [math]\displaystyle{ m }[/math] balls to [math]\displaystyle{ n }[/math] bins. The number of assignments that no two balls share a bin is [math]\displaystyle{ {n\choose m}m! }[/math].

Thus the probability is given by:

[math]\displaystyle{ \begin{align} \Pr[\mathcal{E}] = \frac{{n\choose m}m!}{n^m}. \end{align} }[/math]

Recall that [math]\displaystyle{ {n\choose m}=\frac{n!}{(n-m)!m!} }[/math]. Then

[math]\displaystyle{ \begin{align} \Pr[\mathcal{E}] = \frac{{n\choose m}m!}{n^m} = \frac{n!}{n^m(n-m)!} = \frac{n}{n}\cdot\frac{n-1}{n}\cdot\frac{n-2}{n}\cdots\frac{n-(m-1)}{n} = \prod_{k=1}^{m-1}\left(1-\frac{k}{n}\right). \end{align} }[/math]

There is also a more "probabilistic" argument for the above equation. To be rigorous, we need the following theorem, which holds generally and is very useful for computing the AND of many events.

---

By the definition of conditional probability, [math]\displaystyle{ \Pr[A\mid B]=\frac{\Pr[A\wedge B]}{\Pr[B]} }[/math]. Thus, [math]\displaystyle{ \Pr[A\wedge B] =\Pr[B]\cdot\Pr[A\mid B] }[/math]. This hints us that we can compute the probability of the AND of events by conditional probabilities. Formally, we have the following theorem:

Theorem: Let [math]\displaystyle{ \mathcal{E}_1, \mathcal{E}_2, \ldots, \mathcal{E}_n }[/math] be any [math]\displaystyle{ n }[/math] events. Then [math]\displaystyle{ \begin{align} \Pr\left[\bigwedge_{i=1}^n\mathcal{E}_i\right] &= \prod_{k=1}^n\Pr\left[\mathcal{E}_k \mid \bigwedge_{i\lt k}\mathcal{E}_i\right]. \end{align} }[/math]

Proof: It holds that [math]\displaystyle{ \Pr[A\wedge B] =\Pr[B]\cdot\Pr[A\mid B] }[/math]. Thus, let [math]\displaystyle{ A=\mathcal{E}_n }[/math] and [math]\displaystyle{ B=\mathcal{E}_1\wedge\mathcal{E}_2\wedge\cdots\wedge\mathcal{E}_{n-1} }[/math], then

[math]\displaystyle{ \begin{align} \Pr[\mathcal{E}_1\wedge\mathcal{E}_2\wedge\cdots\wedge\mathcal{E}_n] &= \Pr[\mathcal{E}_1\wedge\mathcal{E}_2\wedge\cdots\wedge\mathcal{E}_{n-1}]\cdot\Pr[\mathcal{E}_n\mid \bigwedge_{i\lt n}\mathcal{E}_i]. \end{align} }[/math]

Recursively applying this equation until there is only [math]\displaystyle{ \mathcal{E}_1 }[/math], the theorem is proved. [math]\displaystyle{ \square }[/math]

---

Now we are back to the probabilistic analysis of the birthday paradox, modeled as a balls-into-bins scenario.

The first ball is assigned into a bin. The probability that the second ball is assigned to a different bin is [math]\displaystyle{ \left(1-\frac{1}{n}\right) }[/math]. Given that the first two balls are assigned to different bins, the probability that the third ball is assigned to a bin different from the first two is [math]\displaystyle{ \left(1-\frac{2}{n}\right) }[/math]. Continuing this on, assuming that the first [math]\displaystyle{ k-1 }[/math] balls are all in different bins, the probability that the [math]\displaystyle{ k }[/math]th bin is assigned to a different bin than the first [math]\displaystyle{ k-1 }[/math], is given by [math]\displaystyle{ \left(1-\frac{k-1}{n}\right) }[/math]. So the probability that all [math]\displaystyle{ m }[/math] balls are in different bins is the product of all these conditional probabilities:

[math]\displaystyle{ \begin{align} \Pr[\mathcal{E}]=\left(1-\frac{1}{n}\right)\cdot \left(1-\frac{2}{n}\right)\cdots \left(1-\frac{m-1}{n}\right) &= \prod_{k=1}^{m-1}\left(1-\frac{k}{n}\right), \end{align} }[/math]

which is the same as what we got by the counting argument.

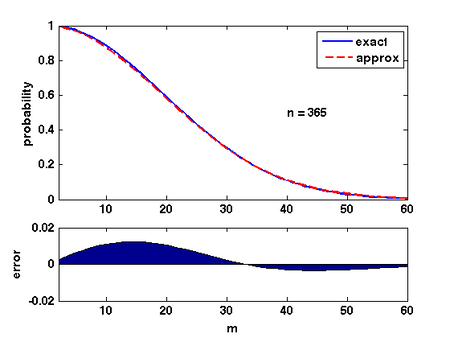
There are several ways of analyzing this formular. Here is a convenient one: Due to Taylor's expansion, [math]\displaystyle{ e^{-k/n}\approx 1-k/n }[/math]. Then

[math]\displaystyle{ \begin{align} \prod_{k=1}^{m-1}\left(1-\frac{k}{n}\right) &\approx \prod_{k=1}^{m-1}e^{-\frac{k}{n}}\\ &= \exp\left(-\sum_{k=1}^{m-1}\frac{k}{n}\right)\\ &= e^{-m(m-1)/2n}\\ &\approx e^{-m^2/2n}. \end{align} }[/math]

The quality of this approximation is shown in the Figure.

Therefore, for [math]\displaystyle{ m=\sqrt{2n\ln \frac{1}{\epsilon}} }[/math], the probability that [math]\displaystyle{ \Pr[\mathcal{E}]\approx\epsilon }[/math].

The occupancy problem

Now we ask about the loads of bins. Assuming that [math]\displaystyle{ m }[/math] balls are uniformly and independently assigned to [math]\displaystyle{ n }[/math] bins, for [math]\displaystyle{ 1\le i\le n }[/math], let [math]\displaystyle{ X_i }[/math] be the load of the [math]\displaystyle{ i }[/math]th bin, i.e. the number of balls in the [math]\displaystyle{ i }[/math]th bin.

First, let us analyze the expected load [math]\displaystyle{ \mathbb{E}[X_i] }[/math] for each bin [math]\displaystyle{ i }[/math].

Because there are totally [math]\displaystyle{ m }[/math] balls, it holds that [math]\displaystyle{ \sum_{i=1}^n X_i=m }[/math].

Therefore, due to the linearity of expectations,

[math]\displaystyle{ \begin{align} \sum_{i=1}^n\mathbb{E}[X_i] &= \mathbb{E}\left[\sum_{i=1}^n X_i\right] = \mathbb{E}\left[m\right] =m. \end{align} }[/math]

Because for each ball, the bin to which the ball is assigned is uniformly and independently chosen, the distributions of the loads of bins are identical. Thus [math]\displaystyle{ \mathbb{E}[X_i] }[/math] is the same for each [math]\displaystyle{ i }[/math]. Combining with the above equation, it holds that for every [math]\displaystyle{ 1\le i\le m }[/math], [math]\displaystyle{ \mathbb{E}[X_i]=\frac{m}{n} }[/math]. So the average is indeed the average!

---

Next we analyze the distribution of the maximum load. We show that when [math]\displaystyle{ m=n }[/math], i.e. [math]\displaystyle{ n }[/math] balls are uniformly and independently thrown into [math]\displaystyle{ n }[/math] bins, the maximum load is [math]\displaystyle{ O\left(\frac{\log n}{\log\log n}\right) }[/math] with high probability.

Theorem: Suppose that [math]\displaystyle{ n }[/math] balls are thrown independently and uniformly at random into [math]\displaystyle{ n }[/math] bins. For [math]\displaystyle{ 1\le i\le n }[/math], let [math]\displaystyle{ X_i }[/math] be the random variable denoting the number of balls in the [math]\displaystyle{ i }[/math]th bin. Then [math]\displaystyle{ \Pr\left[\max_{1\le i\le n}X_i \ge\frac{3\ln n}{\ln\ln n}\right] \lt \frac{1}{n}. }[/math]

Proof: Let [math]\displaystyle{ M }[/math] be an integer. For a particular [math]\displaystyle{ i }[/math], for any particular set of [math]\displaystyle{ M }[/math] balls, these [math]\displaystyle{ M }[/math] balls are all thrown to the [math]\displaystyle{ i }[/math]th bin with probability [math]\displaystyle{ (1/n)^M }[/math], and there are totally [math]\displaystyle{ {n\choose M} }[/math] distinct sets of [math]\displaystyle{ M }[/math] balls. Therefore, applying the union bound, for every [math]\displaystyle{ 1\le i\le n }[/math],

[math]\displaystyle{ \begin{align}\Pr\left[X_i\ge M\right] &\le {n\choose M}\left(\frac{1}{n}\right)^M\\ &= \frac{n!}{M!(n-M)!n^M}\\ &= \frac{1}{M!}\cdot\frac{n(n-1)(n-2)\cdots(n-M+1)}{n^M}\\ &= \frac{1}{M!}\cdot \prod_{i=0}^{M-1}\left(1-\frac{i}{n}\right)\\ &\le \frac{1}{M!}. \end{align} }[/math]

According to Stirling's approximation, [math]\displaystyle{ M!\approx \sqrt{2\pi M}\left(\frac{M}{e}\right)^M }[/math], thus

[math]\displaystyle{ \frac{1}{M!}\le\left(\frac{e}{M}\right)^M. }[/math]

Apply the union bound again,

[math]\displaystyle{ \begin{align} \Pr\left[\max_{1\le i\le n}X_i\ge M\right] &= \Pr\left[X_1\ge M \vee X_2\ge M \vee\cdots\vee X_n\ge M\right]\\ &\le n\Pr[X_1\ge M]\\ &\le n\left(\frac{e}{M}\right)^M. \end{align} }[/math]

When [math]\displaystyle{ M=3\ln n/\ln\ln n }[/math],

[math]\displaystyle{ \begin{align} \left(\frac{e}{M}\right)^M &= \left(\frac{e\ln\ln n}{3\ln n}\right)^{3\ln n/\ln\ln n}\\ &\lt \left(\frac{\ln\ln n}{\ln n}\right)^{3\ln n/\ln\ln n}\\ &= e^{3(\ln\ln\ln n-\ln\ln n)\ln n/\ln\ln n}\\ &\le e^{-3\ln n+3(\ln\ln n)(\ln n)/\ln\ln n}\\ &\le e^{-2\ln n}\\ &= \frac{1}{n^2}. \end{align} }[/math]

Therefore,

[math]\displaystyle{ \begin{align} \Pr\left[\max_{1\le i\le n}X_i\ge \frac{3\ln n}{\ln\ln n}\right] &\le n\left(\frac{e}{M}\right)^M &\lt \frac{1}{n}. \end{align} }[/math]

[math]\displaystyle{ \square }[/math]

Coupon collector's problem

Suppose that a beer company releases [math]\displaystyle{ n }[/math] different types of coupons. Each bottle of contains one coupon with a uniformly random type. Once you have collected all [math]\displaystyle{ n }[/math] types of coupons, you will get a prize. So how many beers you are expected to buy to win the prize?

The coupon collector problem can be described in the balls-into-bins model as follows. We keep throwing balls one-by-one into [math]\displaystyle{ n }[/math] bins (coupons), such that each ball is thrown into a bin uniformly and independently at random. Let [math]\displaystyle{ X }[/math] be the number of balls thrown until no bin is empty. We now determine [math]\displaystyle{ \mathbb{E}[X] }[/math]. It is easy to see it is the same as the coupon collector's problem

Let [math]\displaystyle{ X_i }[/math] be the number of balls thrown while there are exactly [math]\displaystyle{ i-1 }[/math] nonempty bins, then clearly [math]\displaystyle{ \sum_{i=1}^n X_i }[/math].

When there are exactly [math]\displaystyle{ i-1 }[/math] nonempty bins, throwing a ball, the probability that the number of nonempty bins increases (i.e. the ball is thrown to an empty bin) is

[math]\displaystyle{ p_i=1-\frac{i-1}{n}. }[/math]

Thus, [math]\displaystyle{ X_i }[/math] follows the geometric distribution, such that

[math]\displaystyle{ \Pr[X_i=k]=p_i^{k-1}(1-p_i) }[/math]

For a geometric random variable, [math]\displaystyle{ \mathbb{E}[X_i]=\frac{1}{p_i}=\frac{n}{n-i+1} }[/math].

Applying the linearity of expectations,

[math]\displaystyle{ \begin{align} \mathbb{E}[X] &= \mathbb{E}\left[\sum_{i=1}^nX_i\right]\\ &= \sum_{i=1}^n\mathbb{E}\left[X_i\right]\\ &= \sum_{i=1}^n\frac{n}{n-i+1}\\ &= n\sum_{i=1}^n\frac{1}{i}\\ &= nH(n), \end{align} }[/math]

where [math]\displaystyle{ H(n) }[/math] is the [math]\displaystyle{ n }[/math]th Harmonic number, and [math]\displaystyle{ H(n)=\ln n+O(1) }[/math]. Thus, for the coupon collectors problem, the expected number of coupons required to obtain all [math]\displaystyle{ n }[/math] types of coupons is [math]\displaystyle{ n\ln n+O(n) }[/math].