组合数学 (Fall 2024)/Problem Set 2

Problem 1

Count the number of lattice paths from [math]\displaystyle{ (0, 0) }[/math] to [math]\displaystyle{ (n, n) }[/math] with steps up and to the right, when two paths are considered equal if one can be moved on top of the other by a rotation or reflection. For example:

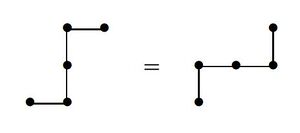
Hint: Represent a path as a sequence of [math]\displaystyle{ 0 }[/math]s and [math]\displaystyle{ 1 }[/math]s and determine the group that acts on these sequences.

Problem 2

Suppose we are given [math]\displaystyle{ m }[/math] [math]\displaystyle{ n }[/math]-sets whose elements are colored with two colors. Two colorings are equal if they arise from each other by a permutation of the [math]\displaystyle{ m }[/math] sets followed by permutations of the individual sets. Determine the number of different colorings using Pólya's enumeration formula. (The answer should be easily verifiable through combinatorial arguments if you get it right!)

Problem 3

Prove the following claims related to Cayley's formula:

• The number of rooted labelled forests with [math]\displaystyle{ n }[/math] vertices is given by [math]\displaystyle{ (n+1)^{n-1} }[/math].

• The number of unrooted labelled forests with [math]\displaystyle{ n }[/math] vertices and [math]\displaystyle{ k }[/math] connected components

such that [math]\displaystyle{ 1,\dots,k }[/math] belong to distinct components is given by [math]\displaystyle{ kn^{n-k-1} }[/math].

• The number of unrooted labelled trees with [math]\displaystyle{ n }[/math] vertices of degrees [math]\displaystyle{ d_1,d_2,\dots,d_n }[/math] respectively is given by [math]\displaystyle{ \binom{n-2}{d_1-1,d_2-1,\dots,d_n-1}=\frac{(n-2)!}{(d_1-1)!(d_2-1)!\cdots(d_n-1)!} }[/math].

Problem 4

There are [math]\displaystyle{ n }[/math] parking spaces [math]\displaystyle{ 1, 2,...,n }[/math] available for [math]\displaystyle{ n }[/math] drivers. Each driver has a favorite space, driver [math]\displaystyle{ i }[/math] space [math]\displaystyle{ f (i) }[/math], [math]\displaystyle{ 1 ≤ f (i) ≤ n }[/math]. The drivers arrive one by one. When driver [math]\displaystyle{ i }[/math] arrives he tries to park his car in space [math]\displaystyle{ f (i) }[/math]. If it is taken he moves down the line to take the first free space greater than [math]\displaystyle{ f (i) }[/math], if any. Example: [math]\displaystyle{ n = 4, f = 3221 }[/math]; then driver [math]\displaystyle{ 1 → 3, 2 → 2, 3 → 4, 4 → 1 }[/math], but for [math]\displaystyle{ f = 2332 }[/math] we have [math]\displaystyle{ 1 → 2, 2 → 3, 3 → 4, 2 →? }[/math] Let [math]\displaystyle{ p(n) }[/math] be the number of sequences [math]\displaystyle{ f }[/math] that allow each driver to park his car; [math]\displaystyle{ f }[/math] is then called a parking sequence. Prove:

• [math]\displaystyle{ f }[/math] is a parking sequence if and only if [math]\displaystyle{ \#\{i : f (i) ≤ k\} ≥ k }[/math].
• [math]\displaystyle{ p(n) = (n + 1)^{n−1} }[/math]. This looks like the number of rooted labelled forests with [math]\displaystyle{ n }[/math] vertices. Can you find a bijection?

Problem 5

For the following problems, provide a formula and explain your answer.

• Count the number of ways to place [math]\displaystyle{ n }[/math] chess pieces on an [math]\displaystyle{ n\times n }[/math] chessboard such that each row, each column, and the main diagonal have at least one chess piece.
• Let [math]\displaystyle{ n }[/math] be even. Count the number of ways to place [math]\displaystyle{ n }[/math] chess pieces on an [math]\displaystyle{ n\times n }[/math] chessboard such that each row, each column, and both diagonals have at least one chess piece.