组合数学 (Fall 2025)/Sieve methods

Principle of Inclusion-Exclusion

Let $A$ and $B$ be two finite sets. The cardinality of their union is

$|A\cup B|=|A|+|B|-|A\cap B|$.

For three sets $A$, $B$, and $C$, the cardinality of the union of these three sets is computed as

$|A\cup B\cup C|=|A|+|B|+|C|-|A\cap B|-|A\cap C|-|B\cap C|+|A\cap B\cap C|$.

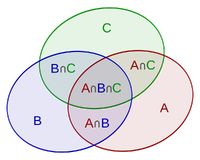
This is illustrated by the following figure.

Generally, the Principle of Inclusion-Exclusion states the rule for computing the union of $n$ finite sets $A_1,A_2,\dots ,A_n$, such that

$\begin{array}{rl}\left|\bigcup _{i=1}^n{A}_i\right|& =\sum _{I\subseteq \{1,\dots ,n\}}(-1{)}^{|I|-1}\left|\bigcap _{i\in I}{A}_i\right|.\end{array}$

---

In combinatorial enumeration, the Principle of Inclusion-Exclusion is usually applied in its complement form.

Let $A_1,A_2,\dots ,A_n\subseteq U$ be subsets of some finite set $U$. Here $U$ is some universe of combinatorial objects, whose cardinality is easy to calculate (e.g. all strings, tuples, permutations), and each $A_i$ contains the objects with some specific property (e.g. a "pattern") which we want to avoid. The problem is to count the number of objects without any of the $n$ properties. We write $\overline{A_i}=U-A_i$. The number of objects without any of the properties $A_1,A_2,\dots ,A_n$ is

$\begin{array}{rl}|\overline{A_1}\cap \overline{A_2}\cap \cdots \cap \overline{A_n}|=|U-\bigcup _{i=1}^n{A}_i|& =|U|+\sum _{I\subseteq \{1,\dots ,n\}}(-1{)}^{|I|}\left|\bigcap _{i\in I}{A}_i\right|.\end{array}$

For an $I\subseteq \{1,2,\dots ,n\}$, we denote

$A_I=\bigcap _{i\in I}{A}_i$

with the convention that $A_{\mathrm{\varnothing }}=U$. The above equation is stated as:

Principle of Inclusion-Exclusion

Let $A_1,A_2,\dots ,A_n$ be a family of subsets of $U$. Then the number of elements of $U$ which lie in none of the subsets $A_i$ is $\sum _{I\subseteq \{1,\dots ,n\}}(-1{)}^{|I|}|A_I|$.

Let $S_k=\sum _{|I|=k}|A_I|$. Conventionally, $S_0=|A_{\mathrm{\varnothing }}|=|U|$. The principle of inclusion-exclusion can be expressed as

$|\overline{A_1}\cap \overline{A_2}\cap \cdots \cap \overline{A_n}|=S_0-S_1+S_2+\cdots +(-1{)}^n{S}_n.$

Surjections

In the twelvefold way, we discuss the counting problems incurred by the mappings $f:N\to M$. The basic case is that elements from both $N$ and $M$ are distinguishable. In this case, it is easy to count the number of arbitrary mappings (which is $m^n$) and the number of injective (one-to-one) mappings (which is $(m{)}_n$), but the number of surjective is difficult. Here we apply the principle of inclusion-exclusion to count the number of surjective (onto) mappings.

Theorem

The number of surjective mappings from an $n$-set to an $m$-set is given by $\sum _{k=1}^m(-1{)}^{m-k}(\genfrac{}{}{0ex}{}{m}{k})k^n$.

Proof. Let $U=\{f:[n]\to [m]\}$ be the set of mappings from $[n]$ to $[m]$. Then $|U|=m^n$. For $i\in [m]$, let $A_i$ be the set of mappings $f:[n]\to [m]$ that none of $j\in [n]$ is mapped to $i$, i.e. $A_i=\{f:[n]\to [m]\setminus \{i\}\}$, thus $|A_i|=(m-1{)}^n$. More generally, for $I\subseteq [m]$, $A_I=\bigcap _{i\in I}{A}_i$ contains the mappings $f:[n]\to [m]\setminus I$. And $|A_I|=(m-|I|{)}^n$. A mapping $f:[n]\to [m]$ is surjective if $f$ lies in none of $A_i$. By the principle of inclusion-exclusion, the number of surjective $f:[n]\to [m]$ is $\sum _{I\subseteq [m]}(-1{)}^{|I|}\left|A_I\right|=\sum _{I\subseteq [m]}(-1{)}^{|I|}(m-|I|{)}^n=\sum _{j=0}^m(-1{)}^j(\genfrac{}{}{0ex}{}{m}{j})(m-j{)}^n$. Let $k=m-j$. The theorem is proved. $◻$

Recall that, in the twelvefold way, we establish a relation between surjections and partitions.

• Surjection to ordered partition:

For a surjective $f:[n]\to [m]$, $(f^{-1}(0),f^{-1}(1),\dots ,f^{-1}(m-1))$ is an ordered partition of $[n]$.

• Ordered partition to surjection:

For an ordered $m$-partition $(B_0,B_1,\dots ,B_{m-1})$ of $[n]$, we can define a function $f:[n]\to [m]$ by letting $f(i)=j$ if and only if $i\in B_j$. $f$ is surjective since as a partition, none of $B_i$ is empty.

Therefore, we have a one-to-one correspondence between surjective mappings from an $n$-set to an $m$-set and the ordered $m$-partitions of an $n$-set.

The Stirling number of the second kind $\left\{\genfrac{}{}{0ex}{}{n}{m}\right\}$ is the number of $m$-partitions of an $n$-set. There are $m!$ ways to order an $m$-partition, thus the number of surjective mappings $f:[n]\to [m]$ is $m!\left\{\genfrac{}{}{0ex}{}{n}{m}\right\}$. Combining with what we have proved for surjections, we give the following result for the Stirling number of the second kind.

Proposition

$\left\{\genfrac{}{}{0ex}{}{n}{m}\right\}=\frac{1}{m!}\sum _{k=1}^m(-1{)}^{m-k}(\genfrac{}{}{0ex}{}{m}{k})k^n$.

Derangements

We now count the number of bijections from a set to itself with no fixed points. This is the derangement problem.

For a permutation $\pi$ of $\{1,2,\dots ,n\}$, a fixed point is such an $i\in \{1,2,\dots ,n\}$ that $\pi (i)=i$. A derangement of $\{1,2,\dots ,n\}$ is a permutation of $\{1,2,\dots ,n\}$ that has no fixed points.

Theorem

The number of derangements of $\{1,2,\dots ,n\}$ given by $n!\sum _{k=0}^n\frac{(-1{)}^k}{k!}\approx \frac{n!}{\mathrm{e}}$.

Proof. Let $U$ be the set of all permutations of $\{1,2,\dots ,n\}$. So $|U|=n!$. Let $A_i$ be the set of permutations with fixed point $i$; so $|A_i|=(n-1)!$. More generally, for any $I\subseteq \{1,2,\dots ,n\}$, $A_I=\bigcap _{i\in I}{A}_i$, and $|A_I|=(n-|I|)!$, since permutations in $A_I$ fix every point in $I$ and permute the remaining points arbitrarily. A permutation is a derangement if and only if it lies in none of the sets $A_i$. So the number of derangements is $\sum _{I\subseteq \{1,2,\dots ,n\}}(-1{)}^{|I|}(n-|I|)!=\sum _{k=0}^n(-1{)}^k(\genfrac{}{}{0ex}{}{n}{k})(n-k)!=n!\sum _{k=0}^n\frac{(-1{)}^k}{k!}.$ By Taylor's series, $\frac{1}{\mathrm{e}}=\sum _{k=0}^{\mathrm{\infty }}\frac{(-1{)}^k}{k!}=\sum _{k=0}^n\frac{(-1{)}^k}{k!}\pm o\left(\frac{1}{n!}\right)$. It is not hard to see that $n!\sum _{k=0}^n\frac{(-1{)}^k}{k!}$ is the closest integer to $\frac{n!}{\mathrm{e}}$. $◻$

Therefore, there are about $\frac{1}{\mathrm{e}}$ fraction of all permutations with no fixed points.

Permutations with restricted positions

We introduce a general theory of counting permutations with restricted positions. In the derangement problem, we count the number of permutations that $\pi (i)\ne i$. We now generalize to the problem of counting permutations which avoid a set of arbitrarily specified positions.

It is traditionally described using terminology from the game of chess. Let $B\subseteq \{1,\dots ,n\}\times \{1,\dots ,n\}$, called a board. As illustrated below, we can think of $B$ as a chess board, with the positions in $B$ marked by "$\times$".

	a	b	c	d	e	f	g	h
8									8
7									7
6									6
5									5
4									4
3									3
2									2
1									1
	a	b	c	d	e	f	g	h

For a permutation $\pi$ of $\{1,\dots ,n\}$, define the graph $G_{\pi }(V,E)$ as

$\begin{array}{rl}{G}_{\pi }& =\{(i,\pi (i))\mid i\in \{1,2,\dots ,n\}\}.\end{array}$

This can also be viewed as a set of marked positions on a chess board. Each row and each column has only one marked position, because $\pi$ is a permutation. Thus, we can identify each $G_{\pi }$ as a placement of $n$ rooks (“城堡”，规则同中国象棋里的“车”) without attacking each other.

For example, the following is the $G_{\pi }$ of such $\pi$ that $\pi (i)=i$.

	a	b	c	d	e	f	g	h
8									8
7									7
6									6
5									5
4									4
3									3
2									2
1									1
	a	b	c	d	e	f	g	h

Now define

$\begin{array}{rl}{N}_0& =\left|\{\pi \mid B\cap G_{\pi }=\mathrm{\varnothing }\}\right|\\ r_k& =\text{number of }k\text{-subsets of }B\text{ such that no two elements have a common coordinate}\\ & =\left|\{S\in (\genfrac{}{}{0ex}{}{B}{k})|\mathrm{\forall }(i_1,j_1),(i_2,j_2)\in S,i_1\ne i_2,j_1\ne j_2\}\right|\end{array}$

Interpreted in chess game,

• $B$: a set of marked positions in an $[n]\times [n]$ chess board.
• $N_0$: the number of ways of placing $n$ non-attacking rooks on the chess board such that none of these rooks lie in $B$.
• $r_k$: number of ways of placing $k$ non-attacking rooks on $B$.

Our goal is to count $N_0$ in terms of $r_k$. This gives the number of permutations avoid all positions in a $B$.

Theorem

$N_0=\sum _{k=0}^n(-1{)}^k{r}_k(n-k)!$.

Proof. For each $i\in [n]$, let $A_i=\{\pi \mid (i,\pi (i))\in B\}$ be the set of permutations $\pi$ whose $i$-th position is in $B$. $N_0$ is the number of permutations avoid all positions in $B$. Thus, our goal is to count the number of permutations $\pi$ in none of $A_i$ for $i\in [n]$. For each $I\subseteq [n]$, let $A_I=\bigcap _{i\in I}{A}_i$, which is the set of permutations $\pi$ such that $(i,\pi (i))\in B$ for all $i\in I$. Due to the principle of inclusion-exclusion, $N_0=\sum _{I\subseteq [n]}(-1{)}^{|I|}|A_I|=\sum _{k=0}^n(-1{)}^k\sum _{I\in (\genfrac{}{}{0ex}{}{[n]}{k})}|A_I|$. The next observation is that $\sum _{I\in (\genfrac{}{}{0ex}{}{[n]}{k})}|A_I|=r_k(n-k)!$, because we can count both sides by first placing $k$ non-attacking rooks on $B$ and placing $n-k$ additional non-attacking rooks on $[n]\times [n]$ in $(n-k)!$ ways. Therefore, $N_0=\sum _{k=0}^n(-1{)}^k{r}_k(n-k)!$. $◻$

Derangement problem

We use the above general method to solve the derange problem again.

Take $B=\{(1,1),(2,2),\dots ,(n,n)\}$ as the chess board. A derangement $\pi$ is a placement of $n$ non-attacking rooks such that none of them is in $B$.

	a	b	c	d	e	f	g	h
8									8
7									7
6									6
5									5
4									4
3									3
2									2
1									1
	a	b	c	d	e	f	g	h

Clearly, the number of ways of placing $k$ non-attacking rooks on $B$ is $r_k=(\genfrac{}{}{0ex}{}{n}{k})$. We want to count $N_0$, which gives the number of ways of placing $n$ non-attacking rooks such that none of these rooks lie in $B$.

By the above theorem

$N_0=\sum _{k=0}^n(-1{)}^k{r}_k(n-k)!=\sum _{k=0}^n(-1{)}^k(\genfrac{}{}{0ex}{}{n}{k})(n-k)!=\sum _{k=0}^n(-1{)}^k\frac{n!}{k!}=n!\sum _{k=0}^n(-1{)}^k\frac{1}{k!}\approx \frac{n!}{e}.$

Problème des ménages

Suppose that in a banquet, we want to seat $n$ couples at a circular table, satisfying the following constraints:

• Men and women are in alternate places.
• No one sits next to his/her spouse.

In how many ways can this be done?

(For convenience, we assume that every seat at the table marked differently so that rotating the seats clockwise or anti-clockwise will end up with a different solution.)

First, let the $n$ ladies find their seats. They may either sit at the odd numbered seats or even numbered seats, in either case, there are $n!$ different orders. Thus, there are $2(n!)$ ways to seat the $n$ ladies.

After sitting the wives, we label the remaining $n$ places clockwise as $0,1,\dots ,n-1$. And a seating of the $n$ husbands is given by a permutation $\pi$ of $[n]$ defined as follows. Let $\pi (i)$ be the seat of the husband of he lady sitting at the $i$-th place.

It is easy to see that $\pi$ satisfies that $\pi (i)\ne i$ and $\pi (i)\not\equiv i+1(\mathrm{mod}n)$, and every permutation $\pi$ with these properties gives a feasible seating of the $n$ husbands. Thus, we only need to count the number of permutations $\pi$ such that $\pi (i)\not\equiv i,i+1(\mathrm{mod}n)$.

Take $B=\{(0,0),(1,1),\dots ,(n-1,n-1),(0,1),(1,2),\dots ,(n-2,n-1),(n-1,0)\}$ as the chess board. A permutation $\pi$ which defines a way of seating the husbands, is a placement of $n$ non-attacking rooks such that none of them is in $B$.

	a	b	c	d	e	f	g	h
8									8
7									7
6									6
5									5
4									4
3									3
2									2
1									1
	a	b	c	d	e	f	g	h

We need to compute $r_k$, the number of ways of placing $k$ non-attacking rooks on $B$. For our choice of $B$, $r_k$ is the number of ways of choosing $k$ points, no two consecutive, from a collection of $2n$ points arranged in a circle.

We first see how to do this in a line.

Lemma

The number of ways of choosing $k$ non-consecutive objects from a collection of $m$ objects arranged in a line, is $(\genfrac{}{}{0ex}{}{m-k+1}{k})$.

Proof. We draw a line of $m-k$ black points, and then insert $k$ red points into the $m-k+1$ spaces between the black points (including the beginning and end). $\begin{array}{rl}& \bigsqcup \bullet \bigsqcup \bullet \bigsqcup \bullet \bigsqcup \bullet \bigsqcup \bullet \bigsqcup \bullet \bigsqcup \bullet \bigsqcup \\ & \Downarrow \\ & \bigsqcup \bullet \bullet \bullet \bullet \bullet \bigsqcup \bullet \bullet \bullet \bigsqcup \bullet \bigsqcup \bullet \bullet \end{array}$ This gives us a line of $m$ points, and the red points specifies the chosen objects, which are non-consecutive. The mapping is 1-1 correspondence. There are $(\genfrac{}{}{0ex}{}{m-k+1}{k})$ ways of placing $k$ red points into $m-k+1$ spaces. $◻$

The problem of choosing non-consecutive objects in a circle can be reduced to the case that the objects are in a line.

Lemma

The number of ways of choosing $k$ non-consecutive objects from a collection of $m$ objects arranged in a circle, is $\frac{m}{m-k}(\genfrac{}{}{0ex}{}{m-k}{k})$.

Proof. Let $f(m,k)$ be the desired number; and let $g(m,k)$ be the number of ways of choosing $k$ non-consecutive points from $m$ points arranged in a circle, next coloring the $k$ points red, and then coloring one of the uncolored point blue. Clearly, $g(m,k)=(m-k)f(m,k)$. But we can also compute $g(m,k)$ as follows: Choose one of the $m$ points and color it blue. This gives us $m$ ways. Cut the circle to make a line of $m-1$ points by removing the blue point. Choose $k$ non-consecutive points from the line of $m-1$ points and color them red. This gives $(\genfrac{}{}{0ex}{}{m-k}{k})$ ways due to the previous lemma. Thus, $g(m,k)=m(\genfrac{}{}{0ex}{}{m-k}{k})$. Therefore we have the desired number $f(m,k)=\frac{m}{m-k}(\genfrac{}{}{0ex}{}{m-k}{k})$. $◻$

By the above lemma, we have that $r_k=\frac{2n}{2n-k}(\genfrac{}{}{0ex}{}{2n-k}{k})$. Then apply the theorem of counting permutations with restricted positions,

$N_0=\sum _{k=0}^n(-1{)}^k{r}_k(n-k)!=\sum _{k=0}^n(-1{)}^k\frac{2n}{2n-k}(\genfrac{}{}{0ex}{}{2n-k}{k})(n-k)!.$

This gives the number of ways of seating the $n$ husbands after the ladies are seated. Recall that there are $2n!$ ways of seating the $n$ ladies. Thus, the total number of ways of seating $n$ couples as required by problème des ménages is

$2n!\sum _{k=0}^n(-1{)}^k\frac{2n}{2n-k}(\genfrac{}{}{0ex}{}{2n-k}{k})(n-k)!.$

Inversion

Posets

A partially ordered set or poset for short is a set $P$ together with a binary relation denoted ${\le }_P$ (or just $\le$ if no confusion is caused), satisfying

• (reflexivity) For all $x\in P,x\le x$.
• (antisymmetry) If $x\le y$ and $y\le x$, then $x=y$.
• (transitivity) If $x\le y$ and $y\le z$, then $x\le z$.

We say two elements $x$ and $y$ are comparable if $x\le y$ or $y\le x$; otherwise $x$ and $y$ are incomparable.

Notation

• $x\ge y$ means $y\le x$.
• $x<y$ means $x\le y$ and $x\ne y$.
• $x>y$ means $y<x$.

The Möbius function

Let $P$ be a finite poset. Consider functions in form of $\alpha :P\times P\to \mathbb{R}$ defined over domain $P\times P$. It is convenient to treat such functions as matrices whose rows and columns are indexed by $P$.

Incidence algebra of poset

Let

$I(P)=\{\alpha :P\times P\to \mathbb{R}\mid \alpha (x,y)=0\text{ for all }x{\nleqq }_{P}y\}$

be the class of $\alpha$ such that $\alpha (x,y)$ is non-zero only for $x{\le }_{P}y$.

Treating $\alpha$ as matrix, it is trivial to see that $I(P)$ is closed under addition and scalar multiplication, that is,

• if $\alpha ,\beta \in I(P)$ then $\alpha +\beta \in I(P)$;
• if $\alpha \in I(P)$ then $c\alpha \in I(P)$ for any $c\in \mathbb{R}$;

where $\alpha ,\beta$ are treated as matrices.

With this spirit, it is natural to define the matrix multiplication in $I(P)$. For $\alpha ,\beta \in I(P)$,

$(\alpha \beta )(x,y)=\sum _{z\in P}\alpha (x,z)\beta (z,y)=\sum _{x\le z\le y}\alpha (x,z)\beta (z,y)$.

The second equation is due to that for $\alpha ,\beta \in I(P)$, for all $z$ other than $x\le z\le y$, $\alpha (x,z)\beta (z,y)$ is zero.

By the transitivity of relation ${\le }_P$, it is also easy to prove that $I(P)$ is closed under matrix multiplication (the detailed proof is left as an exercise). Therefore, $I(P)$ is closed under addition, scalar multiplication and matrix multiplication, so we have an algebra $I(P)$, called incidence algebra, over functions on $P\times P$.

Zeta function and Möbius function

A special function in $I(P)$ is the so-called zeta function $\zeta$, defined as

$\zeta (x,y)=\{\begin{array}{ll}1& \text{if }x{\le }_{P}y,\\ 0& \text{otherwise.}\end{array}$

As a matrix (or more accurately, as an element of the incidence algebra), $\zeta$ is invertible and its inversion, denoted by $\mu$, is called the Möbius function. More precisely, $\mu$ is also in the incidence algebra $I(P)$, and $\mu \zeta =I$ where $I$ is the identity matrix (the identity of the incidence algebra $I(P)$).

There is an equivalent explicit definition of Möbius function.

Definition (Möbius function)

$\mu (x,y)=\{\begin{array}{ll}-\sum _{x\le z<y}\mu (x,z)& \text{if }x<y,\\ 1& \text{if }x=y,\\ 0& \text{if }x\nleqq y.\end{array}$

To see the equivalence between this definition and the inversion of zeta function, we may have the following proposition, which is proved by directly evaluating $\mu \zeta$.

Proposition

For any $x,y\in P$, $\sum _{x\le z\le y}\mu (x,z)=\{\begin{array}{ll}1& \text{if }x=y,\\ 0& \text{otherwise.}\end{array}$

Proof. It holds that $(\mu \zeta )(x,y)=\sum _{x\le z\le y}\mu (x,z)\zeta (z,y)=\sum _{x\le z\le y}\mu (x,z)$. On the other hand, $\mu \zeta =I$, i.e. $(\mu \zeta )(x,y)=\{\begin{array}{ll}1& \text{if }x=y,\\ 0& \text{otherwise.}\end{array}$ The proposition follows. $◻$

Note that $\mu (x,y)=\sum _{x\le z\le y}\mu (x,z)-\sum _{x\le z<y}\mu (x,z)$, which gives the above inductive definition of Möbius function.

Computing Möbius functions

We consider the simple poset $P=[n]$, where $\le$ is the total order. It follows directly from the recursive definition of Möbius function that

$\mu (i,j)=\{\begin{array}{ll}1& \text{if }i=j,\\ -1& \text{if }i+1=j,\\ 0& \text{otherwise.}\end{array}$

Usually for general posets, it is difficult to directly compute the Möbius function from its definition. We introduce a rule helping us compute the Möbius function by decomposing the poset into posets with simple structures.

Theorem (the product rule)

Let $P$ and $Q$ be two finite posets, and $P\times Q$ be the poset resulted from Cartesian product of $P$ and $Q$, where for all $(x,y),(x^{\prime },y^{\prime })\in P\times Q$, $(x,y)\le (x^{\prime },y^{\prime })$ if and only if $x\le x^{\prime }$ and $y\le y^{\prime }$. Then ${\mu }_{P\times Q}((x,y),(x^{\prime },y^{\prime }))={\mu }_P(x,x^{\prime }){\mu }_Q(y,y^{\prime })$.

Proof. We use the recursive definition $\mu (x,y)=\{\begin{array}{ll}-\sum _{x\le z<y}\mu (x,z)& \text{if }x<y,\\ 1& \text{if }x=y,\\ 0& \text{if }x\nleqq y.\end{array}$ to prove the equation in the theorem. If $(x,y)=(x^{\prime },y^{\prime })$, then $x=x^{\prime }$ and $y=y^{\prime }$. It is easy to see that both sides of the equation are 1. If $(x,y)\nleqq (x^{\prime },y^{\prime })$, then either $x\nleqq x^{\prime }$ or $y\nleqq y^{\prime }$. It is also easy to see that both sides are 0. The only remaining case is that $(x,y)<(x^{\prime },y^{\prime })$, in which case either $x<x^{\prime }$ or $y<y^{\prime }$. $\begin{array}{rl}\sum _{(x,y)\le (u,v)\le (x^{\prime },y^{\prime })}{\mu }_P(x,u){\mu }_Q(y,v)& =(\sum _{x\le u\le x^{\prime }}{\mu }_P(x,u))(\sum _{y\le v\le y^{\prime }}{\mu }_Q(y,v))=I(x,x^{\prime })I(y,y^{\prime })=0,\end{array}$ where the last two equations are due to the proposition for $\mu$. Thus ${\mu }_P(x,x^{\prime }){\mu }_Q(y,y^{\prime })=-\sum _{(x,y)\le (u,v)<(x^{\prime },y^{\prime })}{\mu }_P(x,u){\mu }_Q(y,v)$. By induction, assume that the equation ${\mu }_{P\times Q}((x,y),(u,v))={\mu }_P(x,u){\mu }_Q(y,v)$ is true for all $(u,v)<(x^{\prime },y^{\prime })$. Then $\begin{array}{rl}{\mu }_{P\times Q}((x,y),(x^{\prime },y^{\prime }))& =-\sum _{(x,y)\le (u,v)<(x^{\prime },y^{\prime })}{\mu }_{P\times Q}((x,y),(u,v))\\ & =-\sum _{(x,y)\le (u,v)<(x^{\prime },y^{\prime })}{\mu }_P(x,u){\mu }_Q(y,v)\\ & ={\mu }_P(x,x^{\prime }){\mu }_Q(y,y^{\prime }),\end{array}$ which complete the proof. $◻$

Poset of subsets

Consider the poset defined by all subsets of a finite universe $U$, that is $P=2^U$, and for $S,T\subseteq U$, $S{\le }_{P}T$ if and only if $S\subseteq T$.

Möbius function for subsets

The Möbius function for the above defined poset $P$ is that for $S,T\subseteq U$, $\mu (S,T)=\{\begin{array}{ll}(-1{)}^{|T|-|S|}& \text{if }S\subseteq T,\\ 0& \text{otherwise.}\end{array}$

Proof. We can equivalently represent each $S\subseteq U$ by a boolean string $S\in \{0,1{\}}^U$, where $S(x)=1$ if and only if $x\in S$. For each element $x\in U$, we can define a poset $P_x=\{0,1\}$ with $0\le 1$. By definition of Möbius function, the Möbius function of this elementary poset is given by ${\mu }_x(0,0)={\mu }_x(1,1)=1$, ${\mu }_x(0,1)=-1$ and $\mu (1,0)=0$. The poset $P$ of all subsets of $U$ is the Cartesian product of all $P_x$, $x\in U$. By the product rule, $\mu (S,T)=\prod _{x\in U}{\mu }_x(S(x),T(x))=\prod _{\genfrac{}{}{0ex}{}{x\in S}{x\in T}}1\prod _{\genfrac{}{}{0ex}{}{x\notin S}{x\notin T}}1\prod _{\genfrac{}{}{0ex}{}{x\in S}{x\notin T}}0\prod _{\genfrac{}{}{0ex}{}{x\notin S}{x\in T}}(-1)=\{\begin{array}{ll}(-1{)}^{|T|-|S|}& \text{if }S\subseteq T,\\ 0& \text{otherwise.}\end{array}$ $◻$

Note that the poset $P$ is actually the Boolean algebra of rank $|U|$. The proof relies only on that the fact that the poset is a Boolean algebra, thus the theorem holds for Boolean algebra posets.

Posets of divisors

Consider the poset defined by all devisors of a positive integer $n$, that is $P=\{a>0\mid a|n\}$, and for $a,b\in P$, $a{\le }_{P}b$ if and only if $a|b$.

Möbius function for divisors

The Möbius function for the above defined poset $P$ is that for $a,b>0$ that $a|n$ and $b|n$, $\mu (a,b)=\{\begin{array}{ll}(-1{)}^r& \text{if }\frac{b}{a}\text{ is the product of }r\text{ distinct primes},\\ 0& \text{otherwise, i.e. if }a|̸b\text{ or }\frac{b}{a}\text{ is not squarefree.}\end{array}$

Proof. Denote $n=p_1^{n_1}{p}_2^{n_2}\cdots p_k^{n_k}$. Represent $n$ by a tuple $(n_1,n_2,\dots ,n_k)$. Every $a\in P$ corresponds in this way to a tuple $(a_1,a_2,\dots ,a_k)$ with $a_i\le n_i$ for all $1\le i\le k$. Let $P_i=\{1,2,\dots ,n_i\}$ be the poset with $\le$ being the total order. The poset $P$ of divisors of $n$ is thus isomorphic to the poset constructed by the Cartesian product of all $P_i$, $1\le i\le k$. Then $\begin{array}{rl}\mu (a,b)& =\prod _{1\le i\le k}\mu (a_i,b_i)=\prod _{\genfrac{}{}{0ex}{}{1\le i\le k}{a_i=b_i}}1\prod _{\genfrac{}{}{0ex}{}{1\le i\le k}{b_i-a_i=1}}(-1)\prod _{\genfrac{}{}{0ex}{}{1\le i\le k}{b_i-a_i\notin \{0,1\}}}0=\{\begin{array}{ll}(-1{)}^{\sum _i(b_i-a_i)}& \text{if all }{b}_i-a_i\in \{0,1\},\\ 0& \text{otherwise.}\end{array}\\ & =\{\begin{array}{ll}(-1{)}^r& \text{if }\frac{b}{a}\text{ is the product of }r\text{ distinct primes},\\ 0& \text{otherwise.}\end{array}\end{array}$ $◻$

Principle of Möbius inversion

We now introduce the the famous Möbius inversion formula.

Möbius inversion formula

Let $P$ be a finite poset and $\mu$ its Möbius function. Let $f,g:P\to \mathbb{R}$. Then $\mathrm{\forall }x\in P,g(x)=\sum _{y\le x}f(y)$, if and only if $\mathrm{\forall }x\in P,f(x)=\sum _{y\le x}g(y)\mu (y,x)$.

The functions $f,g:P\to \mathbb{R}$ are vectors. Evaluate the matrix multiplications $f\zeta$ and $g\mu$ as follows:

$(f\zeta )(x)=\sum _{y\in P}f(y)\zeta (y,x)=\sum _{y\le x}f(y)$,

and

$(g\mu )(x)=\sum _{y\in P}g(y)\mu (y,x)=\sum _{y\le x}g(y)\mu (y,x)$.

The Möbius inversion formula is nothing but the following statement

$f\zeta =g\iff f=g\mu$,

which is trivially true due to $\mu \zeta =I$ by basic linear algebra.

The following dual form of the inversion formula is also useful.

Möbius inversion formula, dual form

Let $P$ be a finite poset and $\mu$ its Möbius function. Let $f,g:P\to \mathbb{R}$. Then $\mathrm{\forall }x\in P,g(x)=\sum _{y\ge x}f(y)$, if and only if $\mathrm{\forall }x\in P,f(x)=\sum _{y\ge x}\mu (x,y)g(y)$.

To prove the dual form, we only need to evaluate the matrix multiplications on left:

$\zeta f=g\iff f=\mu g$.

Principle of Inclusion-Exclusion

Let $A_1,A_2,\dots ,A_n\subseteq U$. For any $J\subseteq \{1,2,\dots ,n\}$,

• let $f(J)$ be the number of elements that belongs to exactly the sets $A_i,i\in J$ and to no others, i.e.

$f(J)=|\left(\bigcap _{i\in J}{A}_i\right)\setminus \left(\bigcup _{i\notin J}{A}_i\right)|$;

• let $g(J)=\left|\bigcap _{i\in J}{A}_i\right|$.

For any $J\subseteq \{1,2,\dots ,n\}$, the following relation holds for the above defined $f$ and $g$:

$g(J)=\sum _{I\supseteq J}f(I)$.

Applying the dual form of the Möbius inversion formula, we have that for any $J\subseteq \{1,2,\dots ,n\}$,

$f(J)=\sum _{I\supseteq J}\mu (J,I)g(I)=\sum _{I\supseteq J}\mu (J,I)\left|\bigcap _{i\in I}{A}_i\right|$,

where the Möbius function is for the poset of all subsets of $\{1,2,\dots ,n\}$, ordered by $\subseteq$, thus it holds that $\mu (J,I)=(-1{)}^{|I|-|J|}$ for $J\subseteq I$. Therefore,

$f(J)=\sum _{I\supseteq J}(-1{)}^{|I|-|J|}\left|\bigcap _{i\in I}{A}_i\right|$.

We have a formula for the number of elements with exactly those properties $A_i,i\in J$ for any $J\subseteq \{1,2,\dots ,n\}$. For the special case that $J=\mathrm{\varnothing }$, $f(\mathrm{\varnothing })$ is the number of elements satisfying no property of $A_1,A_2,\dots ,A_n$, and

$f(\mathrm{\varnothing })=|U\setminus \bigcup _i{A}_i|=\sum _{I\subseteq \{1,\dots ,n\}}(-1{)}^{|I|}\left|\bigcap _{i\in I}{A}_i\right|$

which gives precisely the Principle of Inclusion-Exclusion.

Möbius inversion formula for number theory

The number-theoretical Möbius inversion formula is stated as such: Let $N$ be a positive integer,

$g(n)=\sum _{d|n}f(d)$ for all $n|N$

if and only if

$f(n)=\sum _{d|n}g(d)\mu \left(\frac{n}{d}\right)$ for all $n|N$,

where $\mu$ is the number-theoretical Möbius function, defined as

$\mu (n)=\{\begin{array}{ll}1& \text{if }n\text{ is product of an even number of distinct primes,}\\ -1& \text{if }n\text{ is product of an odd number of distinct primes,}\\ 0& \text{otherwise.}\end{array}$

The number-theoretical Möbius inversion formula is just a special case of the Möbius inversion formula for posets, when the poset is the set of divisors of $N$, and for any $a,b\in P$, $a{\le }_{P}b$ if $a|b$.

Sieve Method in Number Theory

The Euler totient function

Two integers $m,n$ are said to be relatively prime if their greatest common diviser $\mathrm{g}\mathrm{c}\mathrm{d}(m,n)=1$. For a positive integer $n$, let $\varphi (n)$ be the number of positive integers from $\{1,2,\dots ,n\}$ that are relative prime to $n$. This function, called the Euler $\varphi$ function or the Euler totient function, is fundamental in number theory.

We now derive a formula for this function by using the principle of inclusion-exclusion.

Theorem (The Euler totient function)

Suppose $n$ is divisible by precisely $r$ different primes, denoted $p_1,\dots ,p_r$. Then $\varphi (n)=n\prod _{i=1}^r(1-\frac{1}{p_i})$.

Proof. Let $U=\{1,2,\dots ,n\}$ be the universe. The number of positive integers from $U$ which is divisible by some $p_{i_1},p_{i_2},\dots ,p_{i_s}\in \{p_1,\dots ,p_r\}$, is $\frac{n}{p_{i_1}{p}_{i_2}\cdots p_{i_s}}$. $\varphi (n)$ is the number of integers from $U$ which is not divisible by any $p_1,\dots ,p_r$. By principle of inclusion-exclusion, $\begin{array}{rl}\varphi (n)& =n+\sum _{k=1}^r(-1{)}^k\sum _{1\le i_1<i_2<\cdots <i_k\le n}\frac{n}{p_{i_1}{p}_{i_2}\cdots p_{i_k}}\\ & =n-\sum _{1\le i\le n}\frac{n}{p_i}+\sum _{1\le i<j\le n}\frac{n}{p_i{p}_j}-\sum _{1\le i<j<k\le n}\frac{n}{p_i{p}_j{p}_k}+\cdots +(-1{)}^r\frac{n}{p_1{p}_2\cdots p_r}\\ & =n(1-\sum _{1\le i\le n}\frac{1}{p_i}+\sum _{1\le i<j\le n}\frac{1}{p_i{p}_j}-\sum _{1\le i<j<k\le n}\frac{1}{p_i{p}_j{p}_k}+\cdots +(-1{)}^r\frac{1}{p_1{p}_2\cdots p_r})\\ & =n\prod _{i=1}^r(1-\frac{1}{p_i}).\end{array}$ $◻$

Reference

• Stanley, Enumerative Combinatorics, Volume 1, Chapter 2.
• van Lin and Wilson, A course in combinatorics, Chapter 10, 25.