Randomized Algorithms (Spring 2010)/Hashing, limited independence

Limited Independence

k-wise independence

Recall the definition of independence between events:

Definition (Independent events): Events ${\mathcal{E}}_1,{\mathcal{E}}_2,\dots ,{\mathcal{E}}_n$ are mutually independent if, for any subset $I\subseteq \{1,2,\dots ,n\}$, $\begin{array}{rl}Pr\left[\underset{i\in I}{\bigwedge }{\mathcal{E}}_i\right]& =\prod _{i\in I}Pr[{\mathcal{E}}_i].\end{array}$

Similarly, we can define independence between random variables:

Definition (Independent variables): Random variables $X_1,X_2,\dots ,X_n$ are mutually independent if, for any subset $I\subseteq \{1,2,\dots ,n\}$ and any values $x_i$, where $i\in I$, $\begin{array}{rl}Pr[\underset{i\in I}{\bigwedge }(X_i=x_i)]& =\prod _{i\in I}Pr[X_i=x_i].\end{array}$

Mutual independence is an ideal condition of independence. The limited notion of independence is usually defined by the k-wise independence.

Definition (k-wise Independenc): 1. Events ${\mathcal{E}}_1,{\mathcal{E}}_2,\dots ,{\mathcal{E}}_n$ are k-wise independent if, for any subset $I\subseteq \{1,2,\dots ,n\}$ with $|I|\le k$ $\begin{array}{rl}Pr\left[\underset{i\in I}{\bigwedge }{\mathcal{E}}_i\right]& =\prod _{i\in I}Pr[{\mathcal{E}}_i].\end{array}$ 2. Random variables $X_1,X_2,\dots ,X_n$ are k-wise independent if, for any subset $I\subseteq \{1,2,\dots ,n\}$ with $|I|\le k$ and any values $x_i$, where $i\in I$, $\begin{array}{rl}Pr[\underset{i\in I}{\bigwedge }(X_i=x_i)]& =\prod _{i\in I}Pr[X_i=x_i].\end{array}$

A very common case is pairwise independence, i.e. the 2-wise independence.

Definition (pairwise Independent random variables): Random variables $X_1,X_2,\dots ,X_n$ are pairwise independent if, for any $X_i,X_j$ where $i\ne j$ and any values $a,b$ $\begin{array}{rl}Pr[X_i=a\wedge X_j=b]& =Pr[X_i=a]\cdot Pr[X_j=b].\end{array}$

Note that the definition of k-wise independence is hereditary:

• If $X_1,X_2,\dots ,X_n$ are k-wise independent, then they are also $\ell$-wise independent for any $\ell <k$.
• If $X_1,X_2,\dots ,X_n$ are NOT k-wise independent, then they cannot be $\ell$-wise independent for any $\ell >k$.

Construction via XOR

Suppose we have $m$ mutually independent and uniform random bits $X_1,\dots ,X_m$. We are going to extract $n=2^m-1$ pairwise independent bits from these $m$ mutually independent bits.

Enumerate all the nonempty subsets of $\{1,2,\dots ,m\}$ in some order. Let $S_j$ be the $j$th subset. Let

$Y_j=\underset{i\in S_j}{⨁}{X}_i,$

where $\oplus$ is the exclusive-or, whose truth table is as follows.

$a$	$b$	$a$$\oplus$$b$
0	0	0
0	1	1
1	0	1
1	1	0

There are $n=2^m-1$ such $Y_j$, because there are $2^m-1$ nonempty subsets of $\{1,2,\dots ,m\}$. An equivalent definition of $Y_j$ is

$Y_j=\left(\sum _{i\in S_j}{X}_i\right)mod2$.

Sometimes, $Y_j$ is called the parity of the bits in $S_j$.

We claim that $Y_j$ are pairwise independent and uniform.

Theorem: For any $Y_j$ and any $b\in \{0,1\}$, $\begin{array}{rl}Pr[Y_j=b]& =\frac{1}{2}.\end{array}$ For any $Y_j,Y_{\ell }$ that $j\ne \ell$ and any $a,b\in \{0,1\}$, $\begin{array}{rl}Pr[Y_j=a\wedge Y_{\ell }=b]& =\frac{1}{4}.\end{array}$

The proof is left for your exercise.

Therefore, we extract exponentially many pairwise independent uniform random bits from a sequence of mutually independent uniform random bits.

Note that $Y_j$ are not 3-wise independent. For example, consider the subsets $S_1=\{1\},S_2=\{2\},S_3=\{1,2\}$ and the corresponding random bits $Y_1,Y_2,Y_3$. Any two of $Y_1,Y_2,Y_3$ would decide the value of the third one.

Construction via modulo a prime

We now consider constructing pairwise independent random variables ranging over $[p]=\{0,1,2,\dots ,p-1\}$ for some prime $p$. Unlike the above construction, now we only need two independent random sources $X_0,X_1$, which are uniformly and independently distributed over $[p]$.

Let $Y_0,Y_1,\dots ,Y_{p-1}$ be defined as:

$\begin{array}{rl}{Y}_i=(X_0+i\cdot X_i)modp& \text{for }i\in [p].\end{array}$

Theorem: The random variables $Y_0,Y_1,\dots ,Y_{p-1}$ are pairwise independent uniform random variables over $[p]$.

Proof: We first show that $Y_i$ are uniform. That is, we will show that for any $i,a\in [p]$,

$\begin{array}{rl}Pr[(X_0+i\cdot X_1)modp=a]& =\frac{1}{p}.\end{array}$

Due to the law of total probability,

$\begin{array}{rl}Pr[(X_0+i\cdot X_1)modp=a]& =\sum _{j\in [p]}Pr[X_1=j]\cdot Pr[(X_0+ij)modp=a]\\ & =\frac{1}{p}\sum _{j\in [p]}Pr[X_0\equiv (a-ij)(\mathrm{mod}p)].\end{array}$

For prime $p$, for any $i,j,a\in [p]$, there is exact one value in $[p]$ of $X_0$ satisfying $X_0\equiv (a-ij)(\mathrm{mod}p)$. Thus, $Pr[X_0\equiv (a-ij)(\mathrm{mod}p)]=1/p$ and the above probability is $\frac{1}{p}$.

We then show that $Y_i$ are pairwise independent, i.e. we will show that for any $Y_i,Y_j$ that $i\ne j$ and any $a,b\in [p]$,

$\begin{array}{rl}Pr[Y_i=a\wedge Y_j=b]& =\frac{1}{p^2}.\end{array}$

The event $Y_i=a\wedge Y_j=b$ is equivalent to that

$\{\begin{array}{l}(X_0+i{X}_1)\equiv a(\mathrm{mod}p)\\ (X_0+j{X}_1)\equiv b(\mathrm{mod}p)\end{array}$

Due to the Chinese remainder theorem, there exists a unique solution of $X_0$ and $X_1$ in $[p]$ to the above linear congruential system. Thus the probability of the event is $\frac{1}{p^2}$.

$◻$

Tools for limited independence

For random viables with limited independence, we are not able to directly use the probability tools which rely on the independence of random variables, such as the Chernoff bounds. On the positive side, there are tools that require less independence.

In lecture 4, we show the following theorem of linearity of variance for pairwise independent random variables.

Theorem: For pairwise independent random variables $X_1,X_2,\dots ,X_n$, $\begin{array}{r}\mathbf{V}\mathbf{a}\mathbf{r}\left[\sum _{i=1}^n{X}_i\right]=\sum _{i=1}^n\mathbf{V}\mathbf{a}\mathbf{r}[X_i].\end{array}$

We proved the theorem by showing that the covariances of pairwise independent random variables are 0. The theorem is actually a consequence of a more general statement.

Theorem 1: Let $X_1,X_2,\dots ,X_n$ be mutually independent random variables, $Y_1,Y_2,\dots ,Y_n$ be k-wise independent random variables, and $Pr[X_i=z]=Pr[Y_i=z]$ for every $1\le i\le n$ and any $z$. Let $f:{\mathbb{R}}^n\to \mathbb{R}$ be a multivariate polynomial of degree at most $k$. Then $\begin{array}{r}\mathbf{E}[f(X_1,X_2,\dots ,X_n)]=\mathbf{E}[f(Y_1,Y_2,\dots ,Y_n)].\end{array}$

This phenomenon is sometimes called that the k-degree polynomials are fooled by k-wise independence. In other words, a k-degree polynomial behaves the same on the k-wise independent random variables as on the mutual independent random variables.

This theorem is implied by the following lemma.

Lemma: Let $X_1,X_2,\dots ,X_k$ be $k$ mutually independent random variables. Then $\begin{array}{r}\mathbf{E}\left[\prod _{i=1}^k{X}_i\right]=\prod _{i=1}^k\mathbf{E}[X_i].\end{array}$

The lemma can be proved by directly compute the expectation. We omit the detailed proof.

By the linearity of expectation, the expectation of a polynomial is reduced to the sum of the expectations of terms. For a k-degree polynomial, each term has at most $k$ variables. Due to the above lemma, with k-wise independence, the expectation of each term behaves exactly the same as mutual independence. Theorem 1 is proved.

Since the $k$th moment is the expectation of a k-degree polynomial of random variables, the tools based on the $k$th moment can be safely used for the k-wise independence. In particular, Chebyshev's inequality for pairwise independent random variables:

Chebyshev's inequality: Let $X=\sum _{i=1}^n{X}_i$, where $X_1,X_2,\dots ,X_n$ are pairwise independent Poisson trials. Let $\mu =\mathbf{E}[X]$. Then $Pr[|X-\mu |\ge t]\le \frac{\mathbf{V}\mathbf{a}\mathbf{r}[X]}{t^2}=\frac{\sum _{i=1}^n\mathbf{V}\mathbf{a}\mathbf{r}[X_i]}{t^2}.$

Two-point sampling

Consider a Monte Carlo randomized algorithm with one-sided error for a decision problem $f$. We formulate the algorithm as a deterministic algorithm $A$ that takes as input $x$ and a uniform random number $r\in [p]$ where $p$ is a prime, such that for any input $x$:

• If $f(x)=1$, then $Pr[A(x,r)=1]\ge \frac{1}{2}$, where the probability is taken over the random choice of $r$.
• If $f(x)=0$, then $A(x,r)=0$ for any $r$.

We call $r$ the random source for the algorithm.

For the $x$ that $f(x)=1$, we call the $r$ that makes $A(x,r)=1$ a witness for $x$. For a positive $x$, at least half of $[p]$ are witnesses. The random source $r$ has polynomial number of bits, which means that $p$ is exponentially large, thus it is infeasible to find the witness for an input $x$ by exhaustive search. Deterministic overcomes this by having sophisticated deterministic rules for efficiently searching for a witness. Randomization, on the other hard, reduce this to a bit of luck, by randomly choosing an $r$ and winning with a probability of 1/2.

We can boost the accuracy (equivalently, reduce the error) of any Monte Carlo randomized algorithm with one-sided error by running the algorithm for a number of times.

Suppose that we sample $t$ values $r_1,r_2,\dots ,r_t$ uniformly and independently from $[p]$, and run the following scheme:

$B(x,r_1,r_2,\dots ,r_t):$

return $\underset{i=1}{\overset{t}{\bigvee }}A(x,r_i)$;

That is, return 1 if any instance of $A(x,r_i)=1$. For any $x$ that $f(x)=1$, due to the independence of $r_1,r_2,\dots ,r_t$, the probability that $B(x,r_1,r_2,\dots ,r_t)$ returns an incorrect result is at most $2^{-t}$. On the other hand, $B$ never makes mistakes for the $x$ that $f(x)=0$ since $A$ has no false positives. Thus, the error of the Monte Carlo algorithm is reduced to $2^{-t}$.

Sampling $t$ mutually independent random numbers from $[p]$ can be quite expensive since it requires $\mathrm{\Omega }(t\log p)$ random bits. Suppose that we can only afford $O(\log p)$ random bits. In particular, we sample two independent uniform random number $a$ and $b$ from $[p]$. If we use $a$ and $b$ directly bu running two independent instances $A(x,a)$ and $A(x,b)$, we only get an error upper bound of 1/4.

The following scheme reduces the error significantly with the same number of random bits:

Choose two independent uniform random number $a$ and $b$ from $[p]$. Construct $t$ random number $r_1,r_2,\dots ,r_t$ by: $\begin{array}{rl}\mathrm{\forall }1\le i\le t,& \text{let }{r}_i=(a\cdot i+b)modp.\end{array}$ Run $B(x,r_1,r_2,\dots ,r_t):$.

Due to the discussion in the last section, we know that for $t\le p$, $r_1,r_2,\dots ,r_t$ are pairwise independent and uniform over $[p]$. Let $X_i=A(x,r_i)$ and $X=\sum _{i=1}^t{X}_i$. Due to the uniformity of $r_i$ and our definition of $A$, for any $x$ that $f(x)=1$, it holds that

$Pr[X_i=1]=Pr[A(x,r_i)=1]\ge \frac{1}{2}.$

By the linearity of expectations,

$\mathbf{E}[X]=\sum _{i=1}^t\mathbf{E}[X_i]=\sum _{i=1}^{t}Pr[X_i=1]\ge \frac{t}{2}.$

Since $X_i$ is Bernoulli trial with a probability of success at least $p=1/2$. We can estimate the variance of each $X_i$ as follows.

$\mathbf{V}\mathbf{a}\mathbf{r}[X_i]=p(1-p)\le \frac{1}{4}.$

Applying Chebyshev's inequality, we have that for any $x$ that $f(x)=1$,

$\begin{array}{rl}Pr[\underset{i=1}{\overset{t}{\bigvee }}A(x,r_i)=0]& =Pr[X=0]\\ & \le Pr[|X-\mathbf{E}[X]|\ge \mathbf{E}[X]]\\ & \le Pr[|X-\mathbf{E}[X]|\ge \frac{t}{2}]\\ & \le \frac{4}{t^2}\sum _{i=1}^t\mathbf{V}\mathbf{a}\mathbf{r}[X_i]\\ & \le \frac{1}{t}.\end{array}$

The error is reduced to $1/t$ with only two random numbers. This scheme works as long as $t\le p$.

Hashing

In a hash table, $m$ keys are stored in $n$ slots, and the keys are mapped to slots by a hash function. A collision occurs if two keys are mapped to the same slots. There are various strategies for resolving collisions, such as by chaining, or by "open addressing" techniques like linear probing or double hashing. However, we could also just wish there is no collision.

For hash tables, the hash function is a random mapping from keys to values. To simplify the analysis, we assume that the hash function is uniformly random function $h:U\to [n]$. This assumption is called the Simple Uniform Hash Assumption (SUHA or UHA), which is a standard assumption used in the analysis of hashing

Families of universal hash functions

Carter and Wegman 1977

Definition (universal hash families): Let $U$ be a universe with $|U|\ge n$. A family of hash functions $\mathcal{H}$ from $U$ to $[n]$ is aid to be $k$-universal if, for any elements $x_1,x_2,\dots ,x_k\in U$ and for a hash function $h$ chosen uniformly at random from $\mathcal{H}$, we have $Pr[h(x_1)=h(x_2)=\cdots =h(x_k)]\le \frac{1}{n^{k-1}}.$ A family of hash functions $\mathcal{H}$ from $U$ to $[n]$ is aid to be strongly $k$-universal if, for any elements $x_1,x_2,\dots ,x_k\in U$, any values $y_1,y_2,\dots ,y_k\in [n]$, and for a hash function $h$ chosen uniformly at random from $\mathcal{H}$, we have $Pr[h(x_1)=y_1\wedge h(x_2)=y_2\wedge \cdots \wedge h(x_k)=y_k]=\frac{1}{n^k}.$

In particular, for a 2-universal family $\mathcal{H}$, for any elements $x_1,x_2\in \mathcal{H}$, a uniform random $h\in \mathcal{H}$ has

$Pr[h(x_1)=h(x_2)]\le \frac{1}{n}.$

For a strongly 2-universal family $\mathcal{H}$, for any elements $x_1,x_2\in \mathcal{H}$ and any values $y_1,y_2\in [n]$, a uniform random $h\in \mathcal{H}$ has

$Pr[h(x_1)=y_1\wedge h(x_2)=y_2]=\frac{1}{n^2}.$

This behavior is exactly the same as uniform random hash functions on any pair of inputs. For this reason, a strongly 2-universal hash family are also called pairwise independent hash functions.

Construction of 2-universal family of hash functions

The construction of pairwise independent random variables via modulo a prime introduced in Section 1 already provides a way of constructing a strongly 2-universal hash family.

Let $p$ be a prime. The function $h_{a,b}:[p]\to [p]$ is defined by

$h_{a,b}(x)=(ax+b)modp,$

and the family is

$\mathcal{H}=\{h_{a,b}\mid a,b\in [p]\}.$

Lemma $\mathcal{H}$ is strongly 2-universal.

Proof: In Section 1, we have proved the pairwise independence of the sequence of $(ai+b)modp$, for $i=0,1,\dots ,p-1$, which directly implies that $\mathcal{H}$ is strongly 2-universal.

$◻$

The original construction of Carter-Wegman

What if we want to have hash functions from $[m]$ to $[n]$ for non-prime $m$ and $n$? Carter and Wegman found the following method.

Suppose that the universe is $[m]$, and the functions map $[m]$ to $[n]$, where $m\ge n$. For some prime $p\ge m$, let

$h_{a,b}(x)=((ax+b)modp)modn,$

and the family

$\mathcal{H}=\{h_{a,b}\mid 1\le a\le p-1,b\in [p]\}.$

Note that unlike the first construction, now $a\ne 0$.

Lemma (Carter-Wegman) $\mathcal{H}$ is 2-universal.

A construction used in practice

The main issue of Carter-Wegman construction is the efficiency. The mod operation is very slow, and has been so for more than 30 years.

The following construction is due to Dietzfelbinger et al. It was published in 1997 and has been practically used in various applications of universal hashing.

The family of hash functions is from $[2^u]$ to $[2^v]$. With a binary representation, the functions map binary strings of length $u$ to binary strings of length $v$. Let

$h_a(x)=\lfloor \frac{a\cdot xmod{2}^u}{2^{u-v}}\rfloor ,$

and the family

$\mathcal{H}=\{h_a\mid a\in [2^v]\text{ and }a\text{ is odd}\}.$

This family of hash functions does not exactly meet the requirement of 2-universal family. However, Dietzfelbinger et al proved that $\mathcal{H}$ is close to a 2-universal family. Specifically, for any input values $x_1,x_2\in [2^u]$, for a uniformly random $h\in \mathcal{H}$,

$Pr[h(x_1)=h(x_2)]\le \frac{1}{2^{v-1}}.$

So $\mathcal{H}$ is within an approximation ratio of 2 to being 2-universal.

The function is extremely simple to compute in c language. We exploit that C-multiplication (*) of unsigned u-bit numbers is done $mod{2}^u$, and have a one-line C-code for computing the hash function:

h_a(x) = (a*x)>>(u-v)

The bit-wise shifting is a lot faster than modular. It explains the popularity of this scheme in practice than the original Carter-Wegman construction.

Collision number

Consider a 2-universal family $\mathcal{H}$ of hash functions from $U$ to $[n]$. Let $h$ be a hash function chosen uniformly from $\mathcal{H}$. For a fixed set $S$ of $m$ distinct elements from $U$, say $S=\{x_1,x_2,\dots ,x_m\}$, the elements are mapped to the hash values $h(x_1),h(x_2),\dots ,h(x_m)$. This can be seen as throwing $m$ balls to $n$ bins, with pairwise independent choices of bins.

As in the balls-into-bins with full independence, we are curious about the questions such as the birthday problem or the maximum load. These questions are interesting not only because they are natural to ask in a balls-into-bins setting, but in the context of hashing, they are closely related to the performance of hash functions.

The old techniques for analyzing balls-into-bins rely too much on the independence of the choice of the bin for each ball, therefore can hardly be extended to the setting of 2-universal hash families. However, it turns out several balls-into-bins questions can somehow be answered by analyzing a very natural quantity: the number of collision pairs.

A collision pair for hashing is a pair of elements $x_1,x_2\in S$ which are mapped to the same hash value, i.e. $h(x_1)=h(x_2)$. Formally, for a fixed set of elements $S=\{x_1,x_2,\dots ,x_m\}$, let the random variable

$X_{ij}=\{\begin{array}{ll}1& \text{if }h(x_i)=h(x_j),\\ 0& \text{otherwise.}\end{array}$

The total number of collision pairs among the $m$ elements $x_1,x_2,\dots ,x_m$ is

$X=\sum _{i<j}{X}_{ij}$

Since $\mathcal{H}$ is 2-universal, for any $i\ne j$,

$Pr[X_{ij}=1]=Pr[h(x_i)=h(x_j)]\le \frac{1}{n}.$

The expected number of collision pairs is

$\mathbf{E}[X]=\mathbf{E}\left[\sum _{i<j}{X}_{ij}\right]=\sum _{i<j}\mathbf{E}[X_{ij}]=\sum _{i<j}Pr[X_{ij}=1]\le (\genfrac{}{}{0ex}{}{m}{2})\frac{1}{n}<\frac{m^2}{2n}.$

Birthday problem

In the context of hash functions, the birthday problem ask for the probability that there is no collision at all. Since collision is something that we want to avoid in the applications of hash functions, we would like to lower bound the probability of zero-collision, i.e. to upper bound the probability that there exists a collision pair.

The above analysis gives us an estimation on the expected number of collision pairs, such that $\mathbf{E}[X]<\frac{m^2}{2n}$. Apply the Markov's inequality, for $0<ϵ<1$, we have

$Pr[X\ge \frac{m^2}{2ϵn}]\le Pr[X\ge \frac{1}{ϵ}\mathbf{E}[X]]\le ϵ.$

When $m\le \sqrt{2ϵn}$, the number of collision pairs is $X\ge 1$ with probability at most $ϵ$, therefore with probability at least $1-ϵ$, there is no collision at all. Therefore, we have the following theorem.

Theorem: If $h$ is chosen uniformly from a 2-universal family of hash functions mapping the universe $U$ to $[n]$, then for any set $S\subset U$ of size $m$, where $m=\sqrt{2ϵn}$, $Pr[\text{collision occurs}]\le ϵ.$

Recall that for mutually independent choices of bins, for some $m=\sqrt{2n\ln (1/ϵ)}$, the probability that a collision occurs is about $ϵ$. For constant $ϵ$, this gives an essentially same bound as the pairwise independent setting. Therefore, the behavior of pairwise independent hash function is essentially the same as the uniform random hash function for the birthday problem. This is easy to understand, because birthday problem is about the behavior of collisions, and the definition of 2-universal hash function can be interpreted as "functions that the probability of collision is as low as a uniform random function".

Maximum load

Suppose that a fixed set $S=\{x_1,x_2,\dots ,x_m\}$ of $m$ distinct elements are mapped to random locations $h(x_1),h(x_2),\dots ,h(x_m)$ by a pairwise independent hash function $h$ from $U$ to $[n]$. The load of a location $i\in [n]$ is the number of elements in $S$ mapped to $i$. We want to bound the maximum load.

For uniform random hash function, this is exactly the maximum load in the balls-into-bins game. And we know that for $m=n$, the maximum load is $O(\ln /\ln \ln n)$ with high probability. This bound can be proved either by counting or by the Chernoff bound.

For pairwise independent hash functions, neither of previous techniques works any more. Nevertheless, we find that a bound on the maximum load can be directly implied by our analysis of collision number.

Let $Y$ be a random variable which denotes the maximum load, i.e. the max number of balls in a bin by seeing elements as balls and has values as bins. Then the collision pairs contributed by this heaviest loaded bin is $(\genfrac{}{}{0ex}{}{Y}{2})$, so the total number of collision pairs is at least $(\genfrac{}{}{0ex}{}{Y}{2})$.

By our previous analysis, the expected number of collision pairs is $\mathbf{E}[X]<\frac{m^2}{2n}$. Therefore,

$Pr[(\genfrac{}{}{0ex}{}{Y}{2})\ge \frac{m^2}{2ϵn}]\le Pr[X\ge \frac{1}{ϵ}\mathbf{E}[X]]\le ϵ,$

which implies that

$Pr[Y\ge \frac{m}{\sqrt{ϵn}}]\le ϵ.$

In particular, when $m=n$, the maximum load is at most $\sqrt{2n}$ with probability at least 1/2. This bound is much weaker than the $O(\ln n/\ln \ln n)$ bound for uniform hash functions, but it is extremely general and holds for any 2-universal hash families. In fact, it was show by Alon et al that there exists 2-universal hash families which yields a maximum load that matches the above bound.

• Alon, Dietzfelbinger, Miltersen, Petrank, and Tardos. Linear hash functions. Journal of the ACM (JACM), 1999.

Perfect hashing

Perfect hashing is a data structure for storing a static dictionary. In a static dictionary, a set $S$ of items from the universe $U$ are preprocessed and stored in a table. Once the table is constructed, it will nit be changed any more, but will only be used for search operations: a search for an item gives the location of the item in the table or returns that the item is not in the table. You may think of an application that we store an encyclopedia in a DVD, so that searches are very efficient but there will be no updates to the data.

This problem can be solved by binary search on a sorted table or balanced search trees in $O(\log n)$ time for a set $S$ of $n$ elements. We show how to solve this problem with $O(1)$ time by perfect hashing.

The idea of perfect hashing is that we use a hash function $h$ to map items to different entries of the table, store every item $x\in S$ in the entry $h(x)$, and also store the hash function $h$ in a fixed location in the table (usually the beginning of the table). The algorithm for searching for an item is as follows:

search for $x$ in table $T$:

1. retrieve $h$ from a fixed location in the table;
2. if $x=T[h(x)]$ return $h(x)$; else return NOT_FOUND;

This scheme works as long as that the hash function satisfies the following two conditions:

• The description of $h$ is sufficiently short, so that $h$ can be stored in one entry (or in constant many entries) of the table.
• $h$ has no collisions on $S$, i.e. there is no pair of items $x_1,x_2\in S$ that are mapped to the same value by $h$.

The first condition is easy to guarantee for 2-universal hash families. As shown by Carter-Wegman construction, a 2-universal hash function can be uniquely represented by two integers $a$ and $b$, which can be stored in two entries (or just one, if the word length is sufficiently large) of the table.

Our discussion is now focused on the second condition. We find that it relies on the perfectness of the hash function for a data set $S$.

A hash function $h$ is perfect for a set $S$ of items if $h$ maps all items in $S$ to different values, i.e. there is no collision.

We have shown by the birthday problem for 2-universal hashing that when $n$ items are mapped to $n^2$ values, for an $h$ chosen uniformly from a 2-universal family of hash functions, the probability that a collision occurs is at most 1/2. Thus

$Pr[h\text{ is perfect for }S]\ge \frac{1}{2}$

for a table of $n^2$ entries.

The construction of perfect hashing is straightforward then:

For a set $S$ of $n$ elements:

1. uniformly choose an $h$ from a 2-universal family $\mathcal{H}$; (for Carter-Wegman's construction, it means uniformly choose two integer $1\le a\le p-1$ and $b\in [p]$ for a sufficiently large prime $p$.)
2. check whether $h$ is perfect for $S$;
3. if $h$ is NOT perfect for $S$, start over again; else construct the table;

This is a Las Vegas randomized algorithm, which construct a perfect hashing for a fixed set $S$ with expectedly at most two trials (due to geometric distribution). The resulting data structure is a $O(n^2)$-size static dictionary of $n$ elements which answers every search in deterministic $O(1)$ time.

Advanced Hash Tables

In the last section we see how to use $O(n^2)$ space and constant time for answering search in a set. Now we see how to do it with linear space and constant time. This solves the problem of searching asymptotically optimal for both time and space.

This was once a seemingly impossible task, until Yao published a seminal paper in 1981:

• Yao. Should tables be sorted? Journal of the ACM (JACM), 1981.

The paper shows a possibility of achieving linear space and constant time at the same time by exploiting the power of hashing, but assumes an unrealistically large universe.

FKS perfect hashing

Inspired by Yao's work, Fredman, Komlós, and Szemerédi discover the first linear-space and constant-time static dictionary in a realistic setting:

• Fredman, Komlós, and Szemerédi. Storing a sparse table with O(1) worst case access time. Journal of the ACM (JACM), 1984.

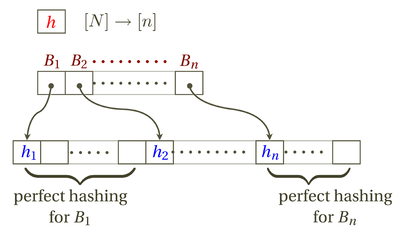
The idea of FKS hashing is to arrange hash table in two levels:

• In the first level, $n$ items are hashed to $n$ buckets by a 2-universal hash function $h$.

Let $B_i$ be the set of items hashed to the $i$th bucket.

• In the second level, construct a $|B_i{|}^2$-size perfect hashing for each bucket $B_i$.

The data structure can be stored in a table. The first few entries are reserved to store the primary hash function $h$. To help the searching algorithm locate a bucket, we use the next $n$ entries of the table as the "pointers" to the bucket: each entry stores the address of the first entry of the space to store a bucket. In the rest of table, the $n$ buckets are stored in order, each using a $|B_i{|}^2$ space as required by perfect hashing.

It is easy to see that the search time is constant. To search for an item $x$, the algorithm does the followings:

• Retrieve $h$.
• Retrieve the address for bucket $h(x)$.
• Search by perfect hashing within bucket $h(x)$.

Each line takes constant time. So the worst-case search time is constant.

We then need to guarantee that the space is linear to $n$. At the first glance, this seems impossible because each instance of perfect hashing for a bucket costs a square-size of space. We will prove that although the individual buckets use square-sized spaces, the sum of the them is still linear.

For a fixed set $S$ of $n$ items, for a hash function $h$ chosen uniformly from a 2-universe family which maps the items to $[n]$, called $n$ buckets, let $Y_i=|B_i|$ be the number of items in $S$ mapped to the $i$th bucket. We are going to bound the following quantity:

$Y=\sum _{i=1}^n{Y}_i^2.$

Since each bucket $B_i$ use a space of $Y_i^2$ for perfect hashing. $Y$ gives the size of the space for storing the buckets.

We will show that $Y$ is related to the total number of collision pairs. (Indeed, the number of collision pairs can be computed by a degree-2 polynomial, just like $Y$.)

Note that a bucket of $Y_i$ items contributes $(\genfrac{}{}{0ex}{}{Y_i}{2})$ collision pairs. Let $X$ be the total number of collision pairs. $X$ can be computed by summing over the collision pairs in every bucket:

$X=\sum _{i=1}^n(\genfrac{}{}{0ex}{}{Y_i}{2})=\sum _{i=1}^n\frac{Y_i(Y_i-1)}{2}=\frac{1}{2}(\sum _{i=1}^n{Y}_i^2-\sum _{i=1}^n{Y}_i)=\frac{1}{2}(\sum _{i=1}^n{Y}_i^2-n).$

Therefore, the sum of squares of the sizes of buckets is related to collision number by:

$\sum _{i=1}^n{Y}_i^2=2X+n.$

By our analysis of the collision number in the last section, we know that for $n$ items mapped to buckets, the expected number of collision pairs is: $\mathbf{E}[X]\le \frac{n}{2}$. Thus,

$\mathbf{E}\left[\sum _{i=1}^n{Y}_i^2\right]=\mathbf{E}[2X+n]\le 2n.$

Due to Markov's inequality, $\sum _{i=1}^n{Y}_i^2=O(n)$ with a constant probability. For any set $S$, we can find a suitable $h$ after expected constant number of trials, and FKS can be constructed with guaranteed (instead of expected) linear-size which answers each search in constant time.

Cuckoo hashing*

Cuckoo hashing also achieves constant search time on a linear space, and after acquiring the hash functions, the accesses to the table can be done in parallel. Cuckoo hashing is considered as a more "modern" hashing technique than FKS by some researchers.

The data structure is defined as follows.

For a set $S$ of $n$ items from the universe:

• A table $T$ of size $s$.
• Two hash functions $h_1$ and $h_2$ are stored separately in fixed places.
• For any item $x\in S$, either $T[h_1(x)]$ or $T[h_2(x)]$ stores $x$.

To search for an item $x$:

• Retrieve $h_1$ and $h_2$ from where they are stored.
• If $T[h_1(x)]=x$, returns $h_1(x)$; If $T[h_2(x)]=x$, returns $h_2(x)$; otherwise, return NOT_FOUND.

After retrieving the hash functions, it accesses the table twice, which can be done in parallel.

We only need to guarantee that it is possible to find a placement of the $n$ items, such that

• each item is placed in one of the two entries it is hashed to;
• no two items are placed into one entry.

This problem can be formulated as a matching problem:

Suppose we have a bipartite graph, where there are $n$ vertices on left and $s$ vertices on right. Each vertex on left corresponds to an item and each vertex on right corresponds to a table entry. An edge connect an item vertex and an entry vertex if at least one of the two hash functions maps the item to the entry. With this reformulation, the problem of finding a feasible placement of items is reduced to finding a matching (edge independent set) of size $n$.

It was shown by Pagh that such a matching exists with constant probability for linear table size $s=O(n)$ when $h_1$ and $h_2$ are drawn uniformly and independently from a $O(\log n)$-universal family of hash functions. We will not describe the detailed proof here.

Bloom filters

Suppose that instead of actually finding the item $x$ in the table, we only want to know whether an item $x$ presents in a set $S$, i.e. answers a very basic question:

"$\text{Is }x\in S?$"

This is called the membership problem, or membership query.

In many applications, the data set can be enormously large, thus the space limit is stringent; on the other hand, the answers need not to be 100% correct, which defines the approximate membership problem. Bloom filter is a space-efficient hash table that solves the approximate membership problem with one-sided error.

Given a set $S$ of $n$ items from the universe $U$, a Bloom filter consists of an array $A$ of $cn$ bits, and $k$ hash functions $h_1,h_2,\dots ,h_k$ maps $U$ to $[cn]$.

Assumption:

• We use the Simple Uniform Hash Assumption and assume $h_1,h_2,\dots ,h_k$ are independent uniform random functions from $U$ to $[cn]$.

The Bloom filter is constructed as follows:

• Initially, all bits in $A$ are 0s.
• For each $x\in S$, let $A[h_i(x)]=1$ for all $1\le i\le k$.

To check if an item $x$ is in $S$, we check whether all array locations $A[h_i(x)]$ for $1\le i\le k$ are set to 1. If not, then obviously $x$ is not a member of $S$. Thus, the Bloom filter has no false negatives.

When all $A[h_i(x)]$ for $1\le i\le k$ are set to 1, it is still possible that $x$ is not in $S$ and the bits are set by other items in $S$. So Bloom filter has false positives. We will bound this probability with the Simple Uniform Hash Assumption.

With the Simple Uniform Hash Assumption, each individual $h_i(x)$ is a uniform and independent sampling of one element of $[cn]$.

After all $n$ items are hashed to Bloom filter, for any specific bit, the probability that the bit is still 0 (survives all $kn$ hashing) is

${(1-\frac{1}{cn})}^{kn}\approx e^{-k/c}.$

For a query $x\notin S$, the $h_i(x)$ are independent of the contents of $A$. The probability that all $A[h_i(x)]$ are 1s (false positive) is

${(1-{(1-\frac{1}{cn})}^{kn})}^k\approx {(1-e^{-k/c})}^k.$

This probability is minimized when $k=c\ln 2$, in which case the probability of false positive is $(0.6185{)}^c.$

Bloom filter solves the membership query with a small constant error of false positives with linear number of bits (instead of linear number of entries).