随机算法 (Fall 2011)/Balls-into-balls Occupancy Problem

Now we ask about the loads of bins. Assuming that $m$ balls are uniformly and independently assigned to $n$ bins, for $1\le i\le n$, let $X_i$ be the load of the $i$th bin, i.e. the number of balls in the $i$th bin.

An easy analysis shows that for every bin $i$, the expected load $\mathbf{E}[X_i]$ is equal to the average load $m/n$.

Because there are totally $m$ balls, it is always true that $\sum _{i=1}^n{X}_i=m$.

Therefore, due to the linearity of expectations,

$\begin{array}{rl}\sum _{i=1}^n\mathbf{E}[X_i]& =\mathbf{E}\left[\sum _{i=1}^n{X}_i\right]=\mathbf{E}\left[m\right]=m.\end{array}$

Because for each ball, the bin to which the ball is assigned is uniformly and independently chosen, the distributions of the loads of bins are identical. Thus $\mathbf{E}[X_i]$ is the same for each $i$. Combining with the above equation, it holds that for every $1\le i\le m$, $\mathbf{E}[X_i]=\frac{m}{n}$. So the average is indeed the average!

---

Next we analyze the distribution of the maximum load. We show that when $m=n$, i.e. $n$ balls are uniformly and independently thrown into $n$ bins, the maximum load is $O\left(\frac{\log n}{\log \log n}\right)$ with high probability.

Theorem

Suppose that $n$ balls are thrown independently and uniformly at random into $n$ bins. For $1\le i\le n$, let $X_i$ be the random variable denoting the number of balls in the $i$th bin. Then $Pr[\underset{1\le i\le n}{max}{X}_i\ge \frac{3\ln n}{\ln \ln n}]<\frac{1}{n}.$

Proof. Let $M$ be an integer. Take bin 1. For any particular $M$ balls, these $M$ balls are all thrown to bin 1 with probability $(1/n{)}^M$, and there are totally $(\genfrac{}{}{0ex}{}{n}{M})$ distinct sets of $M$ balls. Therefore, applying the union bound, $\begin{array}{rl}Pr[X_1\ge M]& \le (\genfrac{}{}{0ex}{}{n}{M}){\left(\frac{1}{n}\right)}^M\\ & =\frac{n!}{M!(n-M)!n^M}\\ & =\frac{1}{M!}\cdot \frac{n(n-1)(n-2)\cdots (n-M+1)}{n^M}\\ & =\frac{1}{M!}\cdot \prod _{i=0}^{M-1}(1-\frac{i}{n})\\ & \le \frac{1}{M!}.\end{array}$ According to Stirling's approximation, $M!\approx \sqrt{2\pi M}{\left(\frac{M}{e}\right)}^M$, thus $\frac{1}{M!}\le {\left(\frac{e}{M}\right)}^M.$ 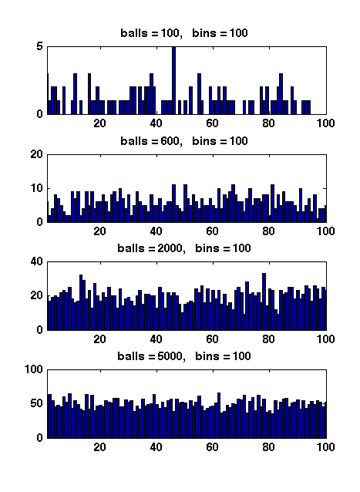Figure 1 Due to the symmetry. All $X_i$ have the same distribution. Apply the union bound again, $\begin{array}{rl}Pr[\underset{1\le i\le n}{max}{X}_i\ge M]& =Pr[(X_1\ge M)\vee (X_2\ge M)\vee \cdots \vee (X_n\ge M)]\\ & \le nPr[X_1\ge M]\\ & \le n{\left(\frac{e}{M}\right)}^M.\end{array}$ When $M=3\ln n/\ln \ln n$, $\begin{array}{rl}{\left(\frac{e}{M}\right)}^M& ={\left(\frac{e\ln \ln n}{3\ln n}\right)}^{3\ln n/\ln \ln n}\\ & <{\left(\frac{\ln \ln n}{\ln n}\right)}^{3\ln n/\ln \ln n}\\ & =e^{3(\ln \ln \ln n-\ln \ln n)\ln n/\ln \ln n}\\ & =e^{-3\ln n+3\ln \ln \ln n\ln n/\ln \ln n}\\ & \le e^{-2\ln n}\\ & =\frac{1}{n^2}.\end{array}$ Therefore, $\begin{array}{rlr}Pr[\underset{1\le i\le n}{max}{X}_i\ge \frac{3\ln n}{\ln \ln n}]& \le n{\left(\frac{e}{M}\right)}^M& <\frac{1}{n}.\end{array}$ $◻$

When $m>n$, Figure 1 illustrates the results of several random experiments, which show that the distribution of the loads of bins becomes more even as the number of balls grows larger than the number of bins.

Formally, it can be proved that for $m=\mathrm{\Omega }(n\log n)$, with high probability, the maximum load is within $O\left(\frac{m}{n}\right)$, which is asymptotically equal to the average load.