随机算法 (Spring 2013)/Random Variables and Expectations

Random Variable

Definition (random variable)

A random variable $X$ on a sample space $\mathrm{\Omega }$ is a real-valued function $X:\mathrm{\Omega }\to \mathbb{R}$. A random variable X is called a discrete random variable if its range is finite or countably infinite.

For a random variable $X$ and a real value $x\in \mathbb{R}$, we write "$X=x$" for the event $\{a\in \mathrm{\Omega }\mid X(a)=x\}$, and denote the probability of the event by

$Pr[X=x]=Pr(\{a\in \mathrm{\Omega }\mid X(a)=x\})$.

The independence can also be defined for variables:

Definition (Independent variables)

Two random variables $X$ and $Y$ are independent if and only if $Pr[(X=x)\wedge (Y=y)]=Pr[X=x]\cdot Pr[Y=y]$ for all values $x$ and $y$. Random variables $X_1,X_2,\dots ,X_n$ are mutually independent if and only if, for any subset $I\subseteq \{1,2,\dots ,n\}$ and any values $x_i$, where $i\in I$, $\begin{array}{rl}Pr[\underset{i\in I}{\bigwedge }(X_i=x_i)]& =\prod _{i\in I}Pr[X_i=x_i].\end{array}$

Note that in probability theory, the "mutual independence" is not equivalent with "pair-wise independence", which we will learn in the future.

Expectation

Let $X$ be a discrete random variable. The expectation of $X$ is defined as follows.

Definition (Expectation)

The expectation of a discrete random variable $X$, denoted by $\mathbf{E}[X]$, is given by $\begin{array}{rl}\mathbf{E}[X]& =\sum _{x}xPr[X=x],\end{array}$ where the summation is over all values $x$ in the range of $X$.

Linearity of Expectation

Perhaps the most useful property of expectation is its linearity.

Theorem (Linearity of Expectations)

For any discrete random variables $X_1,X_2,\dots ,X_n$, and any real constants $a_1,a_2,\dots ,a_n$, $\begin{array}{rl}\mathbf{E}\left[\sum _{i=1}^n{a}_i{X}_i\right]& =\sum _{i=1}^n{a}_i\cdot \mathbf{E}[X_i].\end{array}$

Proof. By the definition of the expectations, it is easy to verify that (try to prove by yourself): for any discrete random variables $X$ and $Y$, and any real constant $c$, $\mathbf{E}[X+Y]=\mathbf{E}[X]+\mathbf{E}[Y]$; $\mathbf{E}[cX]=c\mathbf{E}[X]$. The theorem follows by induction. $◻$

The linearity of expectation gives an easy way to compute the expectation of a random variable if the variable can be written as a sum.

Example

Supposed that we have a biased coin that the probability of HEADs is $p$. Flipping the coin for n times, what is the expectation of number of HEADs?

It looks straightforward that it must be np, but how can we prove it? Surely we can apply the definition of expectation to compute the expectation with brute force. A more convenient way is by the linearity of expectations: Let $X_i$ indicate whether the $i$-th flip is HEADs. Then $\mathbf{E}[X_i]=1\cdot p+0\cdot (1-p)=p$, and the total number of HEADs after n flips is $X=\sum _{i=1}^n{X}_i$. Applying the linearity of expectation, the expected number of HEADs is:

$\mathbf{E}[X]=\mathbf{E}\left[\sum _{i=1}^n{X}_i\right]=\sum _{i=1}^n\mathbf{E}[X_i]=np$.

The real power of the linearity of expectations is that it does not require the random variables to be independent, thus can be applied to any set of random variables. For example:

$\mathbf{E}[\alpha X+\beta X^2+\gamma X^3]=\alpha \cdot \mathbf{E}[X]+\beta \cdot \mathbf{E}\left[X^2\right]+\gamma \cdot \mathbf{E}\left[X^3\right].$

However, do not exaggerate this power!

• For an arbitrary function $f$ (not necessarily linear), the equation $\mathbf{E}[f(X)]=f(\mathbf{E}[X])$ does not hold generally.
• For variances, the equation $var(X+Y)=var(X)+var(Y)$ does not hold without further assumption of the independence of $X$ and $Y$.

Conditional Expectation

Conditional expectation can be accordingly defined:

Definition (conditional expectation)

For random variables $X$ and $Y$, $\mathbf{E}[X\mid Y=y]=\sum _{x}xPr[X=x\mid Y=y],$ where the summation is taken over the range of $X$.

There is also a law of total expectation.

Theorem (law of total expectation)

Let $X$ and $Y$ be two random variables. Then $\mathbf{E}[X]=\sum _y\mathbf{E}[X\mid Y=y]\cdot Pr[Y=y].$

Random Quicksort

Given as input a set $S$ of $n$ numbers, we want to sort the numbers in $S$ in increasing order. One of the most famous algorithm for this problem is the Quicksort algorithm.

• if $|S|>1$ do:
  • pick an $x\in S$ as the pivot;
  • partition $S$ into $S_1$, $\{x\}$, and $S_2$, where all numbers in $S_1$ are smaller than $x$ and all numbers in $S_2$ are larger than $x$;
  • recursively sort $S_1$ and $S_2$;

The time complexity of this sorting algorithm is measured by the number of comparisons.

For the deterministic quicksort algorithm, the pivot is picked from a fixed position (e.g. the first number in the array). The worst-case time complexity in terms of number of comparisons is $\mathrm{\Theta }(n^2)$.

We consider the following randomized version of the quicksort.

• if $|S|>1$ do:
  • uniformly pick a random $x\in S$ as the pivot;
  • partition $S$ into $S_1$, $\{x\}$, and $S_2$, where all numbers in $S_1$ are smaller than $x$ and all numbers in $S_2$ are larger than $x$;
  • recursively sort $S_1$ and $S_2$;

Analysis of Random Quicksort

Our goal is to analyze the expected number of comparisons during an execution of RandQSort with an arbitrary input $S$. We achieve this by measuring the chance that each pair of elements are compared, and summing all of them up due to Linearity of Expectation.

Let $a_i$ denote the $i$th smallest element in $S$. Let $X_{ij}\in \{0,1\}$ be the random variable which indicates whether $a_i$ and $a_j$ are compared during the execution of RandQSort. That is:

$\begin{array}{rl}{X}_{ij}& =\{\begin{array}{ll}1& a_i\text{ and }{a}_j\text{ are compared}\\ 0& \text{otherwise}\end{array}.\end{array}$

Elements $a_i$ and $a_j$ are compared only if one of them is chosen as pivot. After comparison they are separated (thus are never compared again). So we have the following observations:

Observation 1: Every pair of $a_i$ and $a_j$ are compared at most once.

Therefore the sum of $X_{ij}$ for all pair $\{i,j\}$ gives the total number of comparisons. The expected number of comparisons is $\mathbf{E}\left[\sum _{i=1}^n\sum _{j>i}{X}_{ij}\right]$. Due to Linearity of Expectation, $\mathbf{E}\left[\sum _{i=1}^n\sum _{j>i}{X}_{ij}\right]=\sum _{i=1}^n\sum _{j>i}\mathbf{E}\left[X_{ij}\right]$. Our next step is to analyze $\mathbf{E}\left[X_{ij}\right]$ for each $\{i,j\}$.

By the definition of expectation and $X_{ij}$,

$\begin{array}{rl}\mathbf{E}\left[X_{ij}\right]& =1\cdot Pr[a_i\text{ and }{a}_j\text{ are compared}]+0\cdot Pr[a_i\text{ and }{a}_j\text{ are not compared}]\\ & =Pr[a_i\text{ and }{a}_j\text{ are compared}].\end{array}$

We are going to bound this probability.

Observation 2: $a_i$ and $a_j$ are compared if and only if one of them is chosen as pivot when they are still in the same subset.

This is easy to verify: just check the algorithm. The next one is a bit complicated.

Observation 3: If $a_i$ and $a_j$ are still in the same subset then all $\{a_i,a_{i+1},\dots ,a_{j-1},a_j\}$ are in the same subset.

We can verify this by induction. Initially, $S$ itself has the property described above; and partitioning any $S$ with the property into $S_1$ and $S_2$ will preserve the property for both $S_1$ and $S_2$. Therefore Claim 3 holds.

Combining Observation 2 and 3, we have:

Observation 4: $a_i$ and $a_j$ are compared only if one of $\{a_i,a_j\}$ is chosen from $\{a_i,a_{i+1},\dots ,a_{j-1},a_j\}$.

And,

Observation 5: Every one of $\{a_i,a_{i+1},\dots ,a_{j-1},a_j\}$ is chosen equal-probably.

This is because the Random Quicksort chooses the pivot uniformly at random.

Observation 4 and 5 together imply:

$\begin{array}{rl}Pr[a_i\text{ and }{a}_j\text{ are compared}]& \le \frac{2}{j-i+1}.\end{array}$

Remark: Perhaps you feel confused about the above argument. You may ask: "The algorithm chooses pivots for many times during the execution. Why in the above argument, it looks like the pivot is chosen only once?" Good question! Let's see what really happens by looking closely. For any pair $a_i$ and $a_j$, initially $\{a_i,a_{i+1},\dots ,a_{j-1},a_j\}$ are all in the same set $S$ (obviously!). During the execution of the algorithm, the set which containing $\{a_i,a_{i+1},\dots ,a_{j-1},a_j\}$ are shrinking (due to the pivoting), until one of $\{a_i,a_{i+1},\dots ,a_{j-1},a_j\}$ is chosen, and the set is partitioned into different subsets. We ask for the probability that the chosen one is among $\{a_i,a_j\}$. So we really care about "the last" pivoting before $\{a_i,a_{i+1},\dots ,a_{j-1},a_j\}$ is split. Formally, let $Y$ be the random variable denoting the pivot element. We know that for each $a_k\in \{a_i,a_{i+1},\dots ,a_{j-1},a_j\}$, $Y=a_k$ with the same probability, and $Y\notin \{a_i,a_{i+1},\dots ,a_{j-1},a_j\}$ with an unknown probability (remember that there might be other elements in the same subset with $\{a_i,a_{i+1},\dots ,a_{j-1},a_j\}$). The probability we are looking for is actually $Pr[Y\in \{a_i,a_j\}\mid Y\in \{a_i,a_{i+1},\dots ,a_{j-1},a_j\}]$, which is always $\frac{2}{j-i+1}$, provided that $Y$ is uniform over $\{a_i,a_{i+1},\dots ,a_{j-1},a_j\}$. The conditional probability rules out the irrelevant events in a probabilistic argument.

Summing all up:

$\begin{array}{rl}\mathbf{E}\left[\sum _{i=1}^n\sum _{j>i}{X}_{ij}\right]& =\sum _{i=1}^n\sum _{j>i}\mathbf{E}\left[X_{ij}\right]\\ & \le \sum _{i=1}^n\sum _{j>i}\frac{2}{j-i+1}\\ & =\sum _{i=1}^n\sum _{k=2}^{n-i+1}\frac{2}{k}& & (\text{Let }k=j-i+1)\\ & \le \sum _{i=1}^n\sum _{k=1}^n\frac{2}{k}\\ & =2n\sum _{k=1}^n\frac{1}{k}\\ & =2nH(n).\end{array}$

$H(n)$ is the $n$th Harmonic number. It holds that

$\begin{array}{r}H(n)=\ln n+O(1)\end{array}$.

Therefore, for an arbitrary input $S$ of $n$ numbers, the expected number of comparisons taken by RandQSort to sort $S$ is $\mathrm{O}(n\log n)$.

Distributions of Coin Flips

We introduce several important distributions induced by independent coin flips (independent probabilistic experiments), including: Bernoulli trial, geometric distribution, binomial distribution.

Bernoulli trial (Bernoulli distribution)

Bernoulli trial describes the probability distribution of a single (biased) coin flip. Suppose that we flip a (biased) coin where the probability of HEADS is $p$. Let $X$ be the 0-1 random variable which indicates whether the result is HEADS. We say that $X$ follows the Bernoulli distribution with parameter $p$. Formally,

$\begin{array}{rl}X& =\{\begin{array}{ll}1& \text{with probability }p\\ 0& \text{with probability }1-p\end{array}\end{array}$.

Geometric distribution

Suppose we flip the same coin repeatedly until HEADS appears, where each coin flip is independent and follows the Bernoulli distribution with parameter $p$. Let $X$ be the random variable denoting the total number of coin flips. Then $X$ has the geometric distribution with parameter $p$. Formally, $Pr[X=k]=(1-p{)}^{k-1}p$.

For geometric $X$, $\mathbf{E}[X]=\frac{1}{p}$. This can be verified by directly computing $\mathbf{E}[X]$ by the definition of expectations. There is also a smarter way of computing $\mathbf{E}[X]$, by using indicators and the linearity of expectations. For $k=0,1,2,\dots$, let $Y_k$ be the 0-1 random variable such that $Y_k=1$ if and only if none of the first $k$ coin flipings are HEADS, thus $\mathbf{E}[Y_k]=Pr[Y_k=1]=(1-p{)}^k$. A key observation is that $X=\sum _{k=0}^{\mathrm{\infty }}{Y}_k$. Thus, due to the linearity of expectations,

$\begin{array}{r}\mathbf{E}[X]=\mathbf{E}\left[\sum _{k=0}^{\mathrm{\infty }}{Y}_k\right]=\sum _{k=0}^{\mathrm{\infty }}\mathbf{E}[Y_k]=\sum _{k=0}^{\mathrm{\infty }}(1-p{)}^k=\frac{1}{1-(1-p)}=\frac{1}{p}.\end{array}$

Binomial distribution

Suppose we flip the same (biased) coin for $n$ times, where each coin flip is independent and follows the Bernoulli distribution with parameter $p$. Let $X$ be the number of HEADS. Then $X$ has the binomial distribution with parameters $n$ and $p$. Formally, $Pr[X=k]=(\genfrac{}{}{0ex}{}{n}{k})p^k(1-p{)}^{n-k}$.

A binomial random variable $X$ with parameters $n$ and $p$ is usually denoted by $B(n,p)$.

As we saw above, by applying the linearity of expectations, it is easy to show that $\mathbf{E}[X]=np$ for an $X=B(n,p)$.

Balls into Bins

Birthday Problem

There are $m$ students in the class. Assume that for each student, his/her birthday is uniformly and independently distributed over the 365 days in a years. We wonder what the probability that no two students share a birthday.

Due to the pigeonhole principle, it is obvious that for $m>365$, there must be two students with the same birthday. Surprisingly, for any $m>57$ this event occurs with more than 99% probability. This is called the birthday paradox. Despite the name, the birthday paradox is not a real paradox.

We can model this problem as a balls-into-bins problem. $m$ different balls (students) are uniformly and independently thrown into 365 bins (days). More generally, let $n$ be the number of bins. We ask for the probability of the following event $\mathcal{E}$

• $\mathcal{E}$: there is no bin with more than one balls (i.e. no two students share birthday).

We first analyze this by counting. There are totally $n^m$ ways of assigning $m$ balls to $n$ bins. The number of assignments that no two balls share a bin is $(\genfrac{}{}{0ex}{}{n}{m})m!$.

Thus the probability is given by:

$\begin{array}{r}Pr[\mathcal{E}]=\frac{(\genfrac{}{}{0ex}{}{n}{m})m!}{n^m}.\end{array}$

Recall that $(\genfrac{}{}{0ex}{}{n}{m})=\frac{n!}{(n-m)!m!}$. Then

$\begin{array}{r}Pr[\mathcal{E}]=\frac{(\genfrac{}{}{0ex}{}{n}{m})m!}{n^m}=\frac{n!}{n^m(n-m)!}=\frac{n}{n}\cdot \frac{n-1}{n}\cdot \frac{n-2}{n}\cdots \frac{n-(m-1)}{n}=\prod _{k=1}^{m-1}(1-\frac{k}{n}).\end{array}$

There is also a more "probabilistic" argument for the above equation. To be rigorous, we need the following theorem, which holds generally and is very useful for computing the AND of many events.

By the definition of conditional probability, $Pr[A\mid B]=\frac{Pr[A\wedge B]}{Pr[B]}$. Thus, $Pr[A\wedge B]=Pr[B]\cdot Pr[A\mid B]$. This hints us that we can compute the probability of the AND of events by conditional probabilities. Formally, we have the following theorem: Theorem: Let ${\mathcal{E}}_1,{\mathcal{E}}_2,\dots ,{\mathcal{E}}_n$ be any $n$ events. Then $\begin{array}{rl}Pr\left[\underset{i=1}{\overset{n}{\bigwedge }}{\mathcal{E}}_i\right]& =\prod _{k=1}^{n}Pr[{\mathcal{E}}_k\mid \underset{i<k}{\bigwedge }{\mathcal{E}}_i].\end{array}$ Proof: It holds that $Pr[A\wedge B]=Pr[B]\cdot Pr[A\mid B]$. Thus, let $A={\mathcal{E}}_n$ and $B={\mathcal{E}}_1\wedge {\mathcal{E}}_2\wedge \cdots \wedge {\mathcal{E}}_{n-1}$, then $\begin{array}{rl}Pr[{\mathcal{E}}_1\wedge {\mathcal{E}}_2\wedge \cdots \wedge {\mathcal{E}}_n]& =Pr[{\mathcal{E}}_1\wedge {\mathcal{E}}_2\wedge \cdots \wedge {\mathcal{E}}_{n-1}]\cdot Pr[{\mathcal{E}}_n\mid \underset{i<n}{\bigwedge }{\mathcal{E}}_i].\end{array}$ Recursively applying this equation to $Pr[{\mathcal{E}}_1\wedge {\mathcal{E}}_2\wedge \cdots \wedge {\mathcal{E}}_{n-1}]$ until there is only ${\mathcal{E}}_1$ left, the theorem is proved. $◻$

Now we are back to the probabilistic analysis of the birthday problem, with a general setting of $m$ students and $n$ possible birthdays (imagine that we live in a planet where a year has $n$ days).

The first student has a birthday (of course!). The probability that the second student has a different birthday is $(1-\frac{1}{n})$. Given that the first two students have different birthdays, the probability that the third student has a different birthday from the first two is $(1-\frac{2}{n})$. Continuing this on, assuming that the first $k-1$ students all have different birthdays, the probability that the $k$th student has a different birthday than the first $k-1$, is given by $(1-\frac{k-1}{n})$. So the probability that all $m$ students have different birthdays is the product of all these conditional probabilities:

$\begin{array}{rl}Pr[\mathcal{E}]=(1-\frac{1}{n})\cdot (1-\frac{2}{n})\cdots (1-\frac{m-1}{n})& =\prod _{k=1}^{m-1}(1-\frac{k}{n}),\end{array}$

which is the same as what we got by the counting argument.

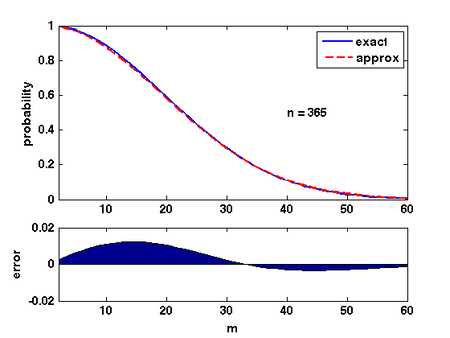
There are several ways of analyzing this formular. Here is a convenient one: Due to Taylor's expansion, $e^{-k/n}\approx 1-k/n$. Then

$\begin{array}{rl}\prod _{k=1}^{m-1}(1-\frac{k}{n})& \approx \prod _{k=1}^{m-1}{e}^{-\frac{k}{n}}\\ & =\exp (-\sum _{k=1}^{m-1}\frac{k}{n})\\ & =e^{-m(m-1)/2n}\\ & \approx e^{-m^2/2n}.\end{array}$

The quality of this approximation is shown in the Figure.

Therefore, for $m=\sqrt{2n\ln \frac{1}{ϵ}}$, the probability that $Pr[\mathcal{E}]\approx ϵ$.

Coupon Collector

Suppose that a chocolate company releases $n$ different types of coupons. Each box of chocolates contains one coupon with a uniformly random type. Once you have collected all $n$ types of coupons, you will get a prize. So how many boxes of chocolates you are expected to buy to win the prize?

The coupon collector problem can be described in the balls-into-bins model as follows. We keep throwing balls one-by-one into $n$ bins (coupons), such that each ball is thrown into a bin uniformly and independently at random. Each ball corresponds to a box of chocolate, and each bin corresponds to a type of coupon. Thus, the number of boxes bought to collect $n$ coupons is just the number of balls thrown until none of the $n$ bins is empty.

Theorem

Let $X$ be the number of balls thrown uniformly and independently to $n$ bins until no bin is empty. Then $\mathbf{E}[X]=nH(n)$, where $H(n)$ is the $n$th harmonic number.

Proof. Let $X_i$ be the number of balls thrown while there are exactly $i-1$ nonempty bins, then clearly $X=\sum _{i=1}^n{X}_i$. When there are exactly $i-1$ nonempty bins, throwing a ball, the probability that the number of nonempty bins increases (i.e. the ball is thrown to an empty bin) is $p_i=1-\frac{i-1}{n}.$ $X_i$ is the number of balls thrown to make the number of nonempty bins increases from $i-1$ to $i$, i.e. the number of balls thrown until a ball is thrown to a current empty bin. Thus, $X_i$ follows the geometric distribution, such that $Pr[X_i=k]=(1-p_i{)}^{k-1}{p}_i$ For a geometric random variable, $\mathbf{E}[X_i]=\frac{1}{p_i}=\frac{n}{n-i+1}$. Applying the linearity of expectations, $\begin{array}{rl}\mathbf{E}[X]& =\mathbf{E}\left[\sum _{i=1}^n{X}_i\right]\\ & =\sum _{i=1}^n\mathbf{E}\left[X_i\right]\\ & =\sum _{i=1}^n\frac{n}{n-i+1}\\ & =n\sum _{i=1}^n\frac{1}{i}\\ & =nH(n),\end{array}$ where $H(n)$ is the $n$th Harmonic number, and $H(n)=\ln n+O(1)$. Thus, for the coupon collectors problem, the expected number of coupons required to obtain all $n$ types of coupons is $n\ln n+O(n)$. $◻$

---

Only knowing the expectation is not good enough. We would like to know how fast the probability decrease as a random variable deviates from its mean value.

Theorem

Let $X$ be the number of balls thrown uniformly and independently to $n$ bins until no bin is empty. Then $Pr[X\ge n\ln n+cn]<e^{-c}$ for any $c>0$.

Proof. For any particular bin $i$, the probability that bin $i$ is empty after throwing $n\ln n+cn$ balls is ${(1-\frac{1}{n})}^{n\ln n+cn}<e^{-(\ln n+c)}=\frac{1}{n{e}^c}.$ By the union bound, the probability that there exists an empty bin after throwing $n\ln n+cn$ balls is $Pr[X\ge n\ln n+cn]<n\cdot \frac{1}{n{e}^c}=e^{-c}.$ $◻$

Occupancy Problem

Now we ask about the loads of bins. Assuming that $m$ balls are uniformly and independently assigned to $n$ bins, for $1\le i\le n$, let $X_i$ be the load of the $i$th bin, i.e. the number of balls in the $i$th bin.

An easy analysis shows that for every bin $i$, the expected load $\mathbf{E}[X_i]$ is equal to the average load $m/n$.

Because there are totally $m$ balls, it is always true that $\sum _{i=1}^n{X}_i=m$.

Therefore, due to the linearity of expectations,

$\begin{array}{rl}\sum _{i=1}^n\mathbf{E}[X_i]& =\mathbf{E}\left[\sum _{i=1}^n{X}_i\right]=\mathbf{E}\left[m\right]=m.\end{array}$

Because for each ball, the bin to which the ball is assigned is uniformly and independently chosen, the distributions of the loads of bins are identical. Thus $\mathbf{E}[X_i]$ is the same for each $i$. Combining with the above equation, it holds that for every $1\le i\le m$, $\mathbf{E}[X_i]=\frac{m}{n}$. So the average is indeed the average!

---

Next we analyze the distribution of the maximum load. We show that when $m=n$, i.e. $n$ balls are uniformly and independently thrown into $n$ bins, the maximum load is $O\left(\frac{\log n}{\log \log n}\right)$ with high probability.

Theorem

Suppose that $n$ balls are thrown independently and uniformly at random into $n$ bins. For $1\le i\le n$, let $X_i$ be the random variable denoting the number of balls in the $i$th bin. Then $Pr[\underset{1\le i\le n}{max}{X}_i\ge \frac{3\ln n}{\ln \ln n}]<\frac{1}{n}.$

Proof. Let $M$ be an integer. Take bin 1. For any particular $M$ balls, these $M$ balls are all thrown to bin 1 with probability $(1/n{)}^M$, and there are totally $(\genfrac{}{}{0ex}{}{n}{M})$ distinct sets of $M$ balls. Therefore, applying the union bound, $\begin{array}{rl}Pr[X_1\ge M]& \le (\genfrac{}{}{0ex}{}{n}{M}){\left(\frac{1}{n}\right)}^M\\ & =\frac{n!}{M!(n-M)!n^M}\\ & =\frac{1}{M!}\cdot \frac{n(n-1)(n-2)\cdots (n-M+1)}{n^M}\\ & =\frac{1}{M!}\cdot \prod _{i=0}^{M-1}(1-\frac{i}{n})\\ & \le \frac{1}{M!}.\end{array}$ According to Stirling's approximation, $M!\approx \sqrt{2\pi M}{\left(\frac{M}{e}\right)}^M$, thus $\frac{1}{M!}\le {\left(\frac{e}{M}\right)}^M.$ 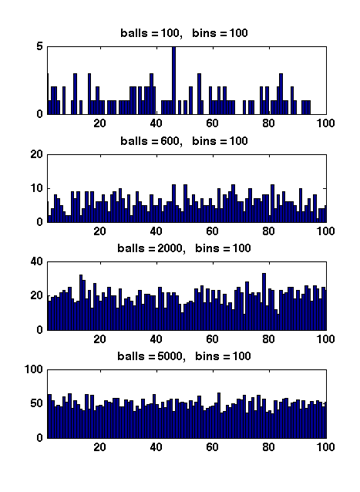Figure 1 Due to the symmetry. All $X_i$ have the same distribution. Apply the union bound again, $\begin{array}{rl}Pr[\underset{1\le i\le n}{max}{X}_i\ge M]& =Pr[(X_1\ge M)\vee (X_2\ge M)\vee \cdots \vee (X_n\ge M)]\\ & \le nPr[X_1\ge M]\\ & \le n{\left(\frac{e}{M}\right)}^M.\end{array}$ When $M=3\ln n/\ln \ln n$, $\begin{array}{rl}{\left(\frac{e}{M}\right)}^M& ={\left(\frac{e\ln \ln n}{3\ln n}\right)}^{3\ln n/\ln \ln n}\\ & <{\left(\frac{\ln \ln n}{\ln n}\right)}^{3\ln n/\ln \ln n}\\ & =e^{3(\ln \ln \ln n-\ln \ln n)\ln n/\ln \ln n}\\ & =e^{-3\ln n+3\ln \ln \ln n\ln n/\ln \ln n}\\ & \le e^{-2\ln n}\\ & =\frac{1}{n^2}.\end{array}$ Therefore, $\begin{array}{rlr}Pr[\underset{1\le i\le n}{max}{X}_i\ge \frac{3\ln n}{\ln \ln n}]& \le n{\left(\frac{e}{M}\right)}^M& <\frac{1}{n}.\end{array}$ $◻$

When $m>n$, Figure 1 illustrates the results of several random experiments, which show that the distribution of the loads of bins becomes more even as the number of balls grows larger than the number of bins.

Formally, it can be proved that for $m=\mathrm{\Omega }(n\log n)$, with high probability, the maximum load is within $O\left(\frac{m}{n}\right)$, which is asymptotically equal to the average load.