随机算法 (Spring 2013)/Threshold and Concentration

Erdős–Rényi Random Graphs

Consider a graph $G(V,E)$ which is randomly generated as:

• $|V|=n$;
• $\mathrm{\forall }\{u,v\}\in (\genfrac{}{}{0ex}{}{V}{2})$, $uv\in E$ independently with probability $p$.

Such graph is denoted as $G(n,p)$. This is called the Erdős–Rényi model or $G(n,p)$ model for random graphs.

Informally, the presence of every edge of $G(n,p)$ is determined by an independent coin flipping (with probability of HEADs $p$).

Monotone properties

A graph property is a predicate of graph which depends only on the structure of the graph.

Definition

Let ${\mathcal{G}}_n=2^{(\genfrac{}{}{0ex}{}{V}{2})}$, where $|V|=n$, be the set of all possible graphs on $n$ vertices. A graph property is a boolean function $P:{\mathcal{G}}_n\to \{0,1\}$ which is invariant under permutation of vertices, i.e. $P(G)=P(H)$ whenever $G$ is isomorphic to $H$.

We are interested in the monotone properties, i.e., those properties that adding edges will not change a graph from having the property to not having the property.

Definition

A graph property $P$ is monotone if for any $G\subseteq H$, both on $n$ vertices, $G$ having property $P$ implies $H$ having property $P$.

By seeing the property as a function mapping a set of edges to a numerical value in $\{0,1\}$, a monotone property is just a monotonically increasing set function.

Some examples of monotone graph properties:

• Hamiltonian;
• $k$-clique;
• contains a subgraph isomorphic to some $H$;
• non-planar;
• chromatic number $>k$ (i.e., not $k$-colorable);
• girth $<\ell$.

From the last two properties, you can see another reason that the Erdős theorem is unintuitive.

Some examples of non-monotone graph properties:

• Eulerian;
• contains an induced subgraph isomorphic to some $H$;

For all monotone graph properties, we have the following theorem.

Theorem

Let $P$ be a monotone graph property. Suppose $G_1=G(n,p_1)$, $G_2=G(n,p_2)$, and $0\le p_1\le p_2\le 1$. Then $Pr[P(G_1)]\le Pr[P(G_2)]$.

Although the statement in the theorem looks very natural, it is difficult to evaluate the probability that a random graph has some property. However, the theorem can be very easily proved by using the idea of coupling, a proof technique in probability theory which compare two unrelated random variables by forcing them to be related.

Proof. For any $\{u,v\}\in (\genfrac{}{}{0ex}{}{[n]}{2})$, let $X_{\{u,v\}}$ be independently and uniformly distributed over the continuous interval $[0,1]$. Let $uv\in G_1$ if and only if $X_{\{u,v\}}\in [0,p_1]$ and let $uv\in G_2$ if and only if $X_{\{u,v\}}\in [0,p_2]$. It is obvious that $G_1\sim G(n,p_1)$ and $G_2\sim G(n,p_2)$. For any $\{u,v\}$, $uv\in G_1$ means that $X_{\{u,v\}}\in [0,p_1]\subseteq [0,p_2]$, which implies that $uv\in G_2$. Thus, $G_1\subseteq G_2$. Since $P$ is monotone, $P(G_1)=1$ implies $P(G_2)$. Thus, $Pr[P(G_1)=1]\le Pr[P(G_2)=1]$. $◻$

Threshold phenomenon

One of the most fascinating phenomenon of random graphs is that for so many natural graph properties, the random graph $G(n,p)$ suddenly changes from almost always not having the property to almost always having the property as $p$ grows in a very small range.

A monotone graph property $P$ is said to have the threshold $p(n)$ if

• when $p\ll p(n)$, $Pr[P(G(n,p))]=0$ as $n\to \mathrm{\infty }$ (also called $G(n,p)$ almost always does not have $P$); and
• when $p\gg p(n)$, $Pr[P(G(n,p))]=1$ as $n\to \mathrm{\infty }$ (also called $G(n,p)$ almost always has $P$).

The classic method for proving the threshold is the so-called second moment method (Chebyshev's inequality).

Threshold for 4-clique

Theorem

The threshold for a random graph $G(n,p)$ to contain a 4-clique is $p=n^{2/3}$.

We formulate the problem as such. For any $4$-subset of vertices $S\in (\genfrac{}{}{0ex}{}{V}{4})$, let $X_S$ be the indicator random variable such that

$X_S=\{\begin{array}{ll}1& S\text{ is a clique},\\ 0& \text{otherwise}.\end{array}$

Let $X=\sum _{S\in (\genfrac{}{}{0ex}{}{V}{4})}{X}_S$ be the total number of 4-cliques in $G$.

It is sufficient to prove the following lemma.

Lemma

If $p=o(n^{-2/3})$, then $Pr[X\ge 1]\to 0$ as $n\to \mathrm{\infty }$. If $p=\omega (n^{-2/3})$, then $Pr[X\ge 1]\to 1$ as $n\to \mathrm{\infty }$.

Proof. The first claim is proved by the first moment (expectation and Markov's inequality) and the second claim is proved by the second moment method (Chebyshev's inequality). Every 4-clique has 6 edges, thus for any $S\in (\genfrac{}{}{0ex}{}{V}{4})$, $\mathbf{E}[X_S]=Pr[X_S=1]=p^6$. By the linearity of expectation, $\mathbf{E}[X]=\sum _{S\in (\genfrac{}{}{0ex}{}{V}{4})}\mathbf{E}[X_S]=(\genfrac{}{}{0ex}{}{n}{4})p^6$. Applying Markov's inequality $Pr[X\ge 1]\le \mathbf{E}[X]=O(n^4{p}^6)=o(1)$, if $p=o(n^{-2/3})$. The first claim is proved. To prove the second claim, it is equivalent to show that $Pr[X=0]=o(1)$ if $p=\omega (n^{-2/3})$. By the Chebyshev's inequality, $Pr[X=0]\le Pr[|X-\mathbf{E}[X]|\ge \mathbf{E}[X]]\le \frac{\mathbf{V}\mathbf{a}\mathbf{r}[X]}{(\mathbf{E}[X]{)}^2}$, where the variance is computed as $\mathbf{V}\mathbf{a}\mathbf{r}[X]=\mathbf{V}\mathbf{a}\mathbf{r}\left[\sum _{S\in (\genfrac{}{}{0ex}{}{V}{4})}{X}_S\right]=\sum _{S\in (\genfrac{}{}{0ex}{}{V}{4})}\mathbf{V}\mathbf{a}\mathbf{r}[X_S]+\sum _{S,T\in (\genfrac{}{}{0ex}{}{V}{4}),S\ne T}\mathbf{C}\mathbf{o}\mathbf{v}(X_S,X_T)$. For any $S\in (\genfrac{}{}{0ex}{}{V}{4})$, $\mathbf{V}\mathbf{a}\mathbf{r}[X_S]=\mathbf{E}[X_S^2]-\mathbf{E}[X_S{]}^2\le \mathbf{E}[X_S^2]=\mathbf{E}[X_S]=p^6$. Thus the first term of above formula is $\sum _{S\in (\genfrac{}{}{0ex}{}{V}{4})}\mathbf{V}\mathbf{a}\mathbf{r}[X_S]=O(n^4{p}^6)$. We now compute the covariances. For any $S,T\in (\genfrac{}{}{0ex}{}{V}{4})$ that $S\ne T$: Case.1: $|S\cap T|\le 1$, so $S$ and $T$ do not share any edges. $X_S$ and $X_T$ are independent, thus $\mathbf{C}\mathbf{o}\mathbf{v}(X_S,X_T)=0$. Case.2: $|S\cap T|=2$, so $S$ and $T$ share an edge. Since $|S\cup T|=6$, there are $(\genfrac{}{}{0ex}{}{n}{6})=O(n^6)$ pairs of such $S$ and $T$. $\mathbf{C}\mathbf{o}\mathbf{v}(X_S,X_T)=\mathbf{E}[X_S{X}_T]-\mathbf{E}[X_S]\mathbf{E}[X_T]\le \mathbf{E}[X_S{X}_T]=Pr[X_S=1\wedge X_T=1]=p^{11}$ since there are 11 edges in the union of two 4-cliques that share a common edge. The contribution of these pairs is $O(n^6{p}^{11})$. Case.2: $|S\cap T|=3$, so $S$ and $T$ share a triangle. Since $|S\cup T|=5$, there are $(\genfrac{}{}{0ex}{}{n}{5})=O(n^5)$ pairs of such $S$ and $T$. By the same argument, $\mathbf{C}\mathbf{o}\mathbf{v}(X_S,X_T)\le Pr[X_S=1\wedge X_T=1]=p^9$ since there are 9 edges in the union of two 4-cliques that share a triangle. The contribution of these pairs is $O(n^5{p}^9)$. Putting all these together, $\mathbf{V}\mathbf{a}\mathbf{r}[X]=O(n^4{p}^6+n^6{p}^{11}+n^5{p}^9).$ And $Pr[X=0]\le \frac{\mathbf{V}\mathbf{a}\mathbf{r}[X]}{(\mathbf{E}[X]{)}^2}=O(n^{-4}{p}^{-6}+n^{-2}{p}^{-1}+n^{-3}{p}^{-3})$, which is $o(1)$ if $p=\omega (n^{-2/3})$. The second claim is also proved. $◻$

Threshold for balanced subgraphs

The above theorem can be generalized to any "balanced" subgraphs.

Definition

The density of a graph $G(V,E)$, denoted $\rho (G)$, is defined as $\rho (G)=\frac{|E|}{|V|}$. A graph $G(V,E)$ is balanced if $\rho (H)\le \rho (G)$ for all subgraphs $H$ of $G$.

Cliques are balanced, because $\frac{(\genfrac{}{}{0ex}{}{k}{2})}{k}\le \frac{(\genfrac{}{}{0ex}{}{n}{2})}{n}$ for any $k\le n$. The threshold for 4-clique is a direct corollary of the following general theorem.

Theorem (Erdős–Rényi 1960)

Let $H$ be a balanced graph with $k$ vertices and $\ell$ edges. The threshold for the property that a random graph $G(n,p)$ contains a (not necessarily induced) subgraph isomorphic to $H$ is $p=n^{-k/\ell }$.

Sketch of proof. For any $S\in (\genfrac{}{}{0ex}{}{V}{k})$, let $X_S$ indicate whether $G_S$ (the subgraph of $G$ induced by $S$) contain a subgraph $H$. Then $p^{\ell }\le \mathbf{E}[X_S]\le k!p^{\ell }$, since there are at most $k!$ ways to match the substructure. Note that $k$ does not depend on $n$. Thus, $\mathbf{E}[X_S]=\mathrm{\Theta }(p^{\ell })$. Let $X=\sum _{S\in (\genfrac{}{}{0ex}{}{V}{k})}{X}_S$ be the number of $H$-subgraphs. $\mathbf{E}[X]=\mathrm{\Theta }(n^k{p}^{\ell })$. By Markov's inequality, $Pr[X\ge 1]\le \mathbf{E}[X]=\mathrm{\Theta }(n^k{p}^{\ell })$ which is $o(1)$ when $p\ll n^{-\ell /k}$. By Chebyshev's inequality, $Pr[X=0]\le \frac{\mathbf{V}\mathbf{a}\mathbf{r}[X]}{\mathbf{E}[X{]}^2}$ where $\mathbf{V}\mathbf{a}\mathbf{r}[X]=\sum _{S\in (\genfrac{}{}{0ex}{}{V}{k})}\mathbf{V}\mathbf{a}\mathbf{r}[X_S]+\sum _{S\ne T}\mathbf{C}\mathbf{o}\mathbf{v}(X_S,X_T)$. The first term $\sum _{S\in (\genfrac{}{}{0ex}{}{V}{k})}\mathbf{V}\mathbf{a}\mathbf{r}[X_S]\le \sum _{S\in (\genfrac{}{}{0ex}{}{V}{k})}\mathbf{E}[X_S^2]=\sum _{S\in (\genfrac{}{}{0ex}{}{V}{k})}\mathbf{E}[X_S]=\mathbf{E}[X]=\mathrm{\Theta }(n^k{p}^{\ell })$. For the covariances, $\mathbf{C}\mathbf{o}\mathbf{v}(X_S,X_T)\ne 0$ only if $|S\cap T|=i$ for $2\le i\le k-1$. Note that $|S\cap T|=i$ implies that $|S\cup T|=2k-i$. And for balanced $H$, the number of edges of interest in $S$ and $T$ is $2\ell -i\rho (H_{S\cap T})\ge 2\ell -i\rho (H)=2\ell -i\ell /k$. Thus, $\mathbf{C}\mathbf{o}\mathbf{v}(X_S,X_T)\le \mathbf{E}[X_S{X}_T]\le p^{2\ell -i\ell /k}$. And, $\sum _{S\ne T}\mathbf{C}\mathbf{o}\mathbf{v}(X_S,X_T)=\sum _{i=2}^{k-1}O(n^{2k-i}{p}^{2\ell -i\ell /k})$ Therefore, when $p\gg n^{-\ell /k}$, $Pr[X=0]\le \frac{\mathbf{V}\mathbf{a}\mathbf{r}[X]}{\mathbf{E}[X{]}^2}\le \frac{\mathrm{\Theta }(n^k{p}^{\ell })+\sum _{i=2}^{k-1}O(n^{2k-i}{p}^{2\ell -i\ell /k})}{\mathrm{\Theta }(n^{2k}{p}^{2\ell })}=\mathrm{\Theta }(n^{-k}{p}^{-\ell })+\sum _{i=2}^{k-1}O(n^{-i}{p}^{-i\ell /k})=o(1)$. $◻$

Chernoff Bound

Suppose that we have a fair coin. If we toss it once, then the outcome is completely unpredictable. But if we toss it, say for 1000 times, then the number of HEADs is very likely to be around 500. This striking phenomenon, illustrated in the right figure, is called the concentration. The Chernoff bound captures the concentration of independent trials.

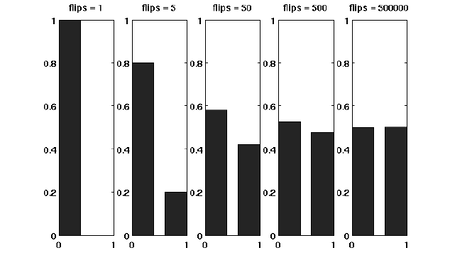
The Chernoff bound is also a tail bound for the sum of independent random variables which may give us exponentially sharp bounds.

Before proving the Chernoff bound, we should talk about the moment generating functions.

Moment generating functions

The more we know about the moments of a random variable $X$, the more information we would have about $X$. There is a so-called moment generating function, which "packs" all the information about the moments of $X$ into one function.

Definition

The moment generating function of a random variable $X$ is defined as $\mathbf{E}\left[{\mathrm{e}}^{\lambda X}\right]$ where $\lambda$ is the parameter of the function.

By Taylor's expansion and the linearity of expectations,

$\begin{array}{rl}\mathbf{E}\left[{\mathrm{e}}^{\lambda X}\right]& =\mathbf{E}\left[\sum _{k=0}^{\mathrm{\infty }}\frac{{\lambda }^k}{k!}{X}^k\right]\\ & =\sum _{k=0}^{\mathrm{\infty }}\frac{{\lambda }^k}{k!}\mathbf{E}\left[X^k\right]\end{array}$

The moment generating function $\mathbf{E}\left[{\mathrm{e}}^{\lambda X}\right]$ is a function of $\lambda$.

The Chernoff bound

The Chernoff bounds are exponentially sharp tail inequalities for the sum of independent trials. The bounds are obtained by applying Markov's inequality to the moment generating function of the sum of independent trials, with some appropriate choice of the parameter $\lambda$.

Chernoff bound (the upper tail)

Let $X=\sum _{i=1}^n{X}_i$, where $X_1,X_2,\dots ,X_n$ are independent Poisson trials. Let $\mu =\mathbf{E}[X]$. Then for any $\delta >0$, $Pr[X\ge (1+\delta )\mu ]\le {\left(\frac{e^{\delta }}{(1+\delta {)}^{(1+\delta )}}\right)}^{\mu }.$

Proof. For any $\lambda >0$, $X\ge (1+\delta )\mu$ is equivalent to that $e^{\lambda X}\ge e^{\lambda (1+\delta )\mu }$, thus $\begin{array}{rl}Pr[X\ge (1+\delta )\mu ]& =Pr[e^{\lambda X}\ge e^{\lambda (1+\delta )\mu }]\\ & \le \frac{\mathbf{E}\left[e^{\lambda X}\right]}{e^{\lambda (1+\delta )\mu }},\end{array}$ where the last step follows by Markov's inequality. Computing the moment generating function $\mathbf{E}[e^{\lambda X}]$: $\begin{array}{rl}\mathbf{E}\left[e^{\lambda X}\right]& =\mathbf{E}\left[e^{\lambda \sum _{i=1}^n{X}_i}\right]\\ & =\mathbf{E}\left[\prod _{i=1}^n{e}^{\lambda X_i}\right]\\ & =\prod _{i=1}^n\mathbf{E}\left[e^{\lambda X_i}\right].& (\text{for independent random variables})\end{array}$ Let $p_i=Pr[X_i=1]$ for $i=1,2,\dots ,n$. Then, $\mu =\mathbf{E}[X]=\mathbf{E}\left[\sum _{i=1}^n{X}_i\right]=\sum _{i=1}^n\mathbf{E}[X_i]=\sum _{i=1}^n{p}_i$. We bound the moment generating function for each individual $X_i$ as follows. $\begin{array}{rl}\mathbf{E}\left[e^{\lambda X_i}\right]& =p_i\cdot e^{\lambda \cdot 1}+(1-p_i)\cdot e^{\lambda \cdot 0}\\ & =1+p_i(e^{\lambda }-1)\\ & \le e^{p_i(e^{\lambda }-1)},\end{array}$ where in the last step we apply the Taylor's expansion so that $e^y\ge 1+y$ where $y=p_i(e^{\lambda }-1)\ge 0$. (By doing this, we can transform the product to the sum of $p_i$, which is $\mu$.) Therefore, $\begin{array}{rl}\mathbf{E}\left[e^{\lambda X}\right]& =\prod _{i=1}^n\mathbf{E}\left[e^{\lambda X_i}\right]\\ & \le \prod _{i=1}^n{e}^{p_i(e^{\lambda }-1)}\\ & =\exp (\sum _{i=1}^n{p}_i(e^{\lambda }-1))\\ & =e^{(e^{\lambda }-1)\mu }.\end{array}$ Thus, we have shown that for any $\lambda >0$, $\begin{array}{rl}Pr[X\ge (1+\delta )\mu ]& \le \frac{\mathbf{E}\left[e^{\lambda X}\right]}{e^{\lambda (1+\delta )\mu }}\\ & \le \frac{e^{(e^{\lambda }-1)\mu }}{e^{\lambda (1+\delta )\mu }}\\ & ={\left(\frac{e^{(e^{\lambda }-1)}}{e^{\lambda (1+\delta )}}\right)}^{\mu }\end{array}$. For any $\delta >0$, we can let $\lambda =\ln (1+\delta )>0$ to get $Pr[X\ge (1+\delta )\mu ]\le {\left(\frac{e^{\delta }}{(1+\delta {)}^{(1+\delta )}}\right)}^{\mu }.$ $◻$

The idea of the proof is actually quite clear: we apply Markov's inequality to $e^{\lambda X}$ and for the rest, we just estimate the moment generating function $\mathbf{E}[e^{\lambda X}]$. To make the bound as tight as possible, we minimized the $\frac{e^{(e^{\lambda }-1)}}{e^{\lambda (1+\delta )}}$ by setting $\lambda =\ln (1+\delta )$, which can be justified by taking derivatives of $\frac{e^{(e^{\lambda }-1)}}{e^{\lambda (1+\delta )}}$.

---

We then proceed to the lower tail, the probability that the random variable deviates below the mean value:

Chernoff bound (the lower tail)

Let $X=\sum _{i=1}^n{X}_i$, where $X_1,X_2,\dots ,X_n$ are independent Poisson trials. Let $\mu =\mathbf{E}[X]$. Then for any $0<\delta <1$, $Pr[X\le (1-\delta )\mu ]\le {\left(\frac{e^{-\delta }}{(1-\delta {)}^{(1-\delta )}}\right)}^{\mu }.$

Proof. For any $\lambda <0$, by the same analysis as in the upper tail version, $\begin{array}{rl}Pr[X\le (1-\delta )\mu ]& =Pr[e^{\lambda X}\ge e^{\lambda (1-\delta )\mu }]\\ & \le \frac{\mathbf{E}\left[e^{\lambda X}\right]}{e^{\lambda (1-\delta )\mu }}\\ & \le {\left(\frac{e^{(e^{\lambda }-1)}}{e^{\lambda (1-\delta )}}\right)}^{\mu }.\end{array}$ For any $0<\delta <1$, we can let $\lambda =\ln (1-\delta )<0$ to get $Pr[X\ge (1-\delta )\mu ]\le {\left(\frac{e^{-\delta }}{(1-\delta {)}^{(1-\delta )}}\right)}^{\mu }.$ $◻$

---

Some useful special forms of the bounds can be derived directly from the above general forms of the bounds. We now know better why we say that the bounds are exponentially sharp.

Useful forms of the Chernoff bound

Let $X=\sum _{i=1}^n{X}_i$, where $X_1,X_2,\dots ,X_n$ are independent Poisson trials. Let $\mu =\mathbf{E}[X]$. Then 1. for $0<\delta \le 1$, $Pr[X\ge (1+\delta )\mu ]<\exp (-\frac{\mu {\delta }^2}{3});$ $Pr[X\le (1-\delta )\mu ]<\exp (-\frac{\mu {\delta }^2}{2});$ 2. for $t\ge 2e\mu$, $Pr[X\ge t]\le 2^{-t}.$

Proof. To obtain the bounds in (1), we need to show that for $0<\delta <1$, $\frac{e^{\delta }}{(1+\delta {)}^{(1+\delta )}}\le e^{-{\delta }^2/3}$ and $\frac{e^{-\delta }}{(1-\delta {)}^{(1-\delta )}}\le e^{-{\delta }^2/2}$. We can verify both inequalities by standard analysis techniques. To obtain the bound in (2), let $t=(1+\delta )\mu$. Then $\delta =t/\mu -1\ge 2e-1$. Hence, $\begin{array}{rl}Pr[X\ge (1+\delta )\mu ]& \le {\left(\frac{e^{\delta }}{(1+\delta {)}^{(1+\delta )}}\right)}^{\mu }\\ & \le {\left(\frac{e}{1+\delta }\right)}^{(1+\delta )\mu }\\ & \le {\left(\frac{e}{2e}\right)}^t\\ & \le 2^{-t}\end{array}$ $◻$

Balls into bins, revisited

Throwing $m$ balls uniformly and independently to $n$ bins, what is the maximum load of all bins with high probability? In the last class, we gave an analysis of this problem by using a counting argument.

Now we give a more "advanced" analysis by using Chernoff bounds.

For any $i\in [n]$ and $j\in [m]$, let $X_{ij}$ be the indicator variable for the event that ball $j$ is thrown to bin $i$. Obviously

$\mathbf{E}[X_{ij}]=Pr[\text{ball }j\text{ is thrown to bin }i]=\frac{1}{n}$

Let $Y_i=\sum _{j\in [m]}{X}_{ij}$ be the load of bin $i$.

Then the expected load of bin $i$ is

$(\ast )\mu =\mathbf{E}[Y_i]=\mathbf{E}\left[\sum _{j\in [m]}{X}_{ij}\right]=\sum _{j\in [m]}\mathbf{E}[X_{ij}]=m/n.$

For the case $m=n$, it holds that $\mu =1$

Note that $Y_i$ is a sum of $m$ mutually independent indicator variable. Applying Chernoff bound, for any particular bin $i\in [n]$,

$Pr[Y_i>(1+\delta )\mu ]\le {\left(\frac{e^{\delta }}{(1+\delta {)}^{1+\delta }}\right)}^{\mu }.$

When $m=n$

When $m=n$, $\mu =1$. Write $c=1+\delta$. The above bound can be written as

$Pr[Y_i>c]\le \frac{e^{c-1}}{c^c}.$

Let $c=\frac{e\ln n}{\ln \ln n}$, we evaluate $\frac{e^{c-1}}{c^c}$ by taking logarithm to its reciprocal.

$\begin{array}{rl}\ln \left(\frac{c^c}{e^{c-1}}\right)& =c\ln c-c+1\\ & =c(\ln c-1)+1\\ & =\frac{e\ln n}{\ln \ln n}(\ln \ln n-\ln \ln \ln n)+1\\ & \ge \frac{e\ln n}{\ln \ln n}\cdot \frac{2}{e}\ln \ln n+1\\ & \ge 2\ln n.\end{array}$

Thus,

$Pr[Y_i>\frac{e\ln n}{\ln \ln n}]\le \frac{1}{n^2}.$

Applying the union bound, the probability that there exists a bin with load $>12\ln n$ is

$n\cdot Pr[Y_1>\frac{e\ln n}{\ln \ln n}]\le \frac{1}{n}$.

Therefore, for $m=n$, with high probability, the maximum load is $O\left(\frac{e\ln n}{\ln \ln n}\right)$.

For larger $m$

When $m\ge n\ln n$, then according to $(\ast )$, $\mu =\frac{m}{n}\ge \ln n$

We can apply an easier form of the Chernoff bounds,

$Pr[Y_i\ge 2e\mu ]\le 2^{-2e\mu }\le 2^{-2e\ln n}<\frac{1}{n^2}.$

By the union bound, the probability that there exists a bin with load $\ge 2e\frac{m}{n}$ is,

$n\cdot Pr[Y_1>2e\frac{m}{n}]=n\cdot Pr[Y_1>2e\mu ]\le \frac{1}{n}$.

Therefore, for $m\ge n\ln n$, with high probability, the maximum load is $O\left(\frac{m}{n}\right)$.