随机算法 (Fall 2015)/Identity Testing

Checking Matrix Multiplication

The evolution of time complexity [math]\displaystyle{ O(n^{\omega}) }[/math] for matrix multiplication.

Let [math]\displaystyle{ \mathbb{F} }[/math] be a feild (you may think of it as the filed [math]\displaystyle{ \mathbb{Q} }[/math] of rational numbers, or the finite field [math]\displaystyle{ \mathbb{Z}_p }[/math] of integers modulo prime [math]\displaystyle{ p }[/math]). We suppose that each field operation (addition, subtraction, multiplication, division) has unit cost. This model is called the unit-cost RAM model, which is an ideal abstraction of a computer.

Consider the following problem:

• Input: Three [math]\displaystyle{ n\times n }[/math] matrices [math]\displaystyle{ A }[/math], [math]\displaystyle{ B }[/math], and [math]\displaystyle{ C }[/math] over the field [math]\displaystyle{ \mathbb{F} }[/math].
• Output: "yes" if [math]\displaystyle{ C=AB }[/math] and "no" if otherwise.

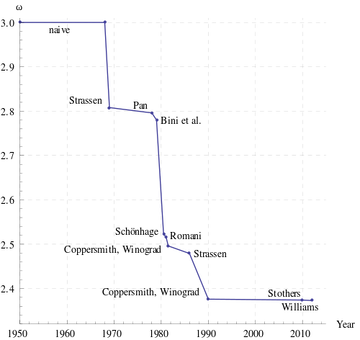
A naive way to solve this is to multiply [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math] and compare the result with [math]\displaystyle{ C }[/math]. The straightforward algorithm for matrix multiplication takes [math]\displaystyle{ O(n^3) }[/math] time, assuming that each arithmetic operation takes unit time. The Strassen's algorithm discovered in 1969 now implemented by many numerical libraries runs in time [math]\displaystyle{ O(n^{\log_2 7})\approx O(n^{2.81}) }[/math]. Strassen's algorithm starts the search for fast matrix multiplication algorithms. The Coppersmith–Winograd algorithm discovered in 1987 runs in time [math]\displaystyle{ O(n^{2.376}) }[/math] but is only faster than Strassens' algorithm on extremely large matrices due to the very large constant coefficient. This has been the best known for decades, until recently Stothers got an [math]\displaystyle{ O(n^{2.3737}) }[/math] algorithm in his PhD thesis in 2010, and independently Vassilevska Williams got an [math]\displaystyle{ O(n^{2.3727}) }[/math] algorithm in 2012. Both these improvements are based on generalization of Coppersmith–Winograd algorithm. It is unknown whether the matrix multiplication can be done in time [math]\displaystyle{ O(n^{2+o(1)}) }[/math].

Freivalds Algorithm

The following is a very simple randomized algorithm due to Freivalds, running in [math]\displaystyle{ O(n^2) }[/math] time:

Algorithm (Freivalds, 1979)

pick a vector [math]\displaystyle{ r \in\{0, 1\}^n }[/math] uniformly at random; if [math]\displaystyle{ A(Br) = Cr }[/math] then return "yes" else return "no";

The product [math]\displaystyle{ A(Br) }[/math] is computed by first multiplying [math]\displaystyle{ Br }[/math] and then [math]\displaystyle{ A(Br) }[/math]. The running time of Freivalds algorithm is [math]\displaystyle{ O(n^2) }[/math] because the algorithm computes 3 matrix-vector multiplications.

If [math]\displaystyle{ AB=C }[/math] then [math]\displaystyle{ A(Br) = Cr }[/math] for any [math]\displaystyle{ r \in\{0, 1\}^n }[/math], thus the algorithm will return a "yes" for any positive instance ([math]\displaystyle{ AB=C }[/math]). But if [math]\displaystyle{ AB \neq C }[/math] then the algorithm will make a mistake if it chooses such an [math]\displaystyle{ r }[/math] that [math]\displaystyle{ ABr = Cr }[/math]. However, the following lemma states that the probability of this event is bounded.

Lemma

If [math]\displaystyle{ AB\neq C }[/math] then for a uniformly random [math]\displaystyle{ r \in\{0, 1\}^n }[/math], [math]\displaystyle{ \Pr[ABr = Cr]\le \frac{1}{2} }[/math].

Proof. Let [math]\displaystyle{ D=AB-C }[/math]. The event [math]\displaystyle{ ABr=Cr }[/math] is equivalent to that [math]\displaystyle{ Dr=0 }[/math]. It is then sufficient to show that for a [math]\displaystyle{ D\neq \boldsymbol{0} }[/math], it holds that [math]\displaystyle{ \Pr[Dr = \boldsymbol{0}]\le \frac{1}{2} }[/math]. Since [math]\displaystyle{ D\neq \boldsymbol{0} }[/math], it must have at least one non-zero entry. Suppose that [math]\displaystyle{ D_{ij}\neq 0 }[/math]. We assume the event that [math]\displaystyle{ Dr=\boldsymbol{0} }[/math]. In particular, the [math]\displaystyle{ i }[/math]-th entry of [math]\displaystyle{ Dr }[/math] is [math]\displaystyle{ (Dr)_{i}=\sum_{k=1}^n D_{ik}r_k=0. }[/math] The [math]\displaystyle{ r_j }[/math] can be calculated by [math]\displaystyle{ r_j=-\frac{1}{D_{ij}}\sum_{k\neq j}^n D_{ik}r_k. }[/math] Once all other entries [math]\displaystyle{ r_k }[/math] with [math]\displaystyle{ k\neq j }[/math] are fixed, there is a unique solution of [math]\displaystyle{ r_j }[/math]. Therefore, the number of [math]\displaystyle{ r\in\{0,1\}^n }[/math] satisfying [math]\displaystyle{ Dr=\boldsymbol{0} }[/math] is at most [math]\displaystyle{ 2^{n-1} }[/math]. The probability that [math]\displaystyle{ ABr=Cr }[/math] is bounded as [math]\displaystyle{ \Pr[ABr=Cr]=\Pr[Dr=\boldsymbol{0}]\le\frac{2^{n-1}}{2^n}=\frac{1}{2} }[/math]. [math]\displaystyle{ \square }[/math]

When [math]\displaystyle{ AB=C }[/math], Freivalds algorithm always returns "yes"; and when [math]\displaystyle{ AB\neq C }[/math], Freivalds algorithm returns "no" with probability at least 1/2.

To improve its accuracy, we can run Freivalds algorithm for [math]\displaystyle{ k }[/math] times, each time with an independent [math]\displaystyle{ r\in\{0,1\}^n }[/math], and return "yes" if and only if all running instances returns "yes".

Freivalds' Algorithm (multi-round)

pick [math]\displaystyle{ k }[/math] vectors [math]\displaystyle{ r_1,r_2,\ldots,r_k \in\{0, 1\}^n }[/math] uniformly and independently at random; if [math]\displaystyle{ A(Br_i) = Cr_i }[/math] for all [math]\displaystyle{ i=1,\ldots,k }[/math] then return "yes" else return "no";

If [math]\displaystyle{ AB=C }[/math], then the algorithm returns a "yes" with probability 1. If [math]\displaystyle{ AB\neq C }[/math], then due to the independence, the probability that all [math]\displaystyle{ r_i }[/math] have [math]\displaystyle{ ABr_i=C_i }[/math] is at most [math]\displaystyle{ 2^{-k} }[/math], so the algorithm returns "no" with probability at least [math]\displaystyle{ 1-2^{-k} }[/math]. For any [math]\displaystyle{ 0\lt \epsilon\lt 1 }[/math], choose [math]\displaystyle{ k=\log_2 \frac{1}{\epsilon} }[/math]. The algorithm runs in time [math]\displaystyle{ O(n^2\log_2\frac{1}{\epsilon}) }[/math] and has a one-sided error (false positive) bounded by [math]\displaystyle{ \epsilon }[/math].

Polynomial Identity Testing (PIT)

Consider the following problem of Polynomial Identity Testing (PIT):

• Input: two polynomials [math]\displaystyle{ P_1, P_2\in\mathbb{F}[x] }[/math] of degree [math]\displaystyle{ d }[/math].
• Output: "yes" if two polynomials are identical, i.e. [math]\displaystyle{ P_1\equiv P_2 }[/math], and "no" if otherwise.

The [math]\displaystyle{ \mathbb{F}[x] }[/math] denote the ring of polynomials over field [math]\displaystyle{ \mathbb{F} }[/math].

Alternatively, we can consider the following equivalent problem:

• Input: a polynomial [math]\displaystyle{ P\in\mathbb{F}[x] }[/math] of degree [math]\displaystyle{ d }[/math].
• Output: "yes" if [math]\displaystyle{ P\equiv 0 }[/math], and "no" if otherwise.

The probalem is trivial if [math]\displaystyle{ P }[/math] is presented in its explicit form [math]\displaystyle{ P(x)=\sum_{i=0}^d a_ix^i }[/math]. But we assume that [math]\displaystyle{ P }[/math] is given in product form or as black box.

A straightforward deterministic algorithm that solves PIT is to query [math]\displaystyle{ d+1 }[/math] points [math]\displaystyle{ P(1),P(2),\ldots,P(d+1) }[/math] and check whether thay are all zero. This can determine whether [math]\displaystyle{ P\equiv 0 }[/math] by interpolation.

We now introduce a simple randomized algorithm for the problem.

Algorithm for PIT

pick [math]\displaystyle{ x\in\{1,2,\ldots,2d\} }[/math] uniformly at random; if [math]\displaystyle{ P(x) = 0 }[/math] then return “yes” else return “no”;

This algorithm requires only the evaluation of [math]\displaystyle{ P }[/math] at a single point. And if [math]\displaystyle{ P\equiv 0 }[/math] it is always correct. And if [math]\displaystyle{ P\not\equiv 0 }[/math] then the probability that the algorithm wrongly returns "yes" is bounded as follows.

Theorem

Let [math]\displaystyle{ P\in\mathbb{F}[x] }[/math] be a polynomial of degree [math]\displaystyle{ d }[/math] over the field [math]\displaystyle{ \mathbb{F} }[/math]. Let [math]\displaystyle{ S\subset\mathbb{F} }[/math] be an arbitrary set and [math]\displaystyle{ x\in S }[/math] is chosen uniformly at random from [math]\displaystyle{ S }[/math]. If [math]\displaystyle{ P\not\equiv 0 }[/math] then [math]\displaystyle{ \Pr[P(x)=0]\le\frac{d}{|S|}. }[/math]

Proof. A non-zero [math]\displaystyle{ d }[/math]-degree polynomial [math]\displaystyle{ P }[/math] has at most [math]\displaystyle{ d }[/math] distinct roots, thus at most [math]\displaystyle{ d }[/math] members [math]\displaystyle{ x }[/math] of [math]\displaystyle{ S }[/math] satisfy that [math]\displaystyle{ P(x)=0 }[/math]. Therefore, [math]\displaystyle{ \Pr[P(x)=0]\le\frac{d}{|S|} }[/math]. [math]\displaystyle{ \square }[/math]

By the theorem, the algorithm can distinguish a non-zero polynomial from 0 with probability at least [math]\displaystyle{ 1/2 }[/math]. This is achieved by evaluation of the polynomial at only one point and [math]\displaystyle{ 1+\log_2 d }[/math] many random bits.

Communication Complexity of Identity

The communication complexity is introduced by Andrew Chi-Chih Yao as a model of computation which involves multiple participants, each with partial information of the input.

Assume that there are two entities, say Alice and Bob. Alice has a private input [math]\displaystyle{ a }[/math] and Bob has a private input [math]\displaystyle{ b }[/math]. Together they want to compute a function [math]\displaystyle{ f(a,b) }[/math] by communicating with each other. The communication follows a predefined communication protocol (the "algorithm" in this model) whose logics depends only on the problem [math]\displaystyle{ f }[/math] but not on the inputs. The complexity of a communication protocol is measured by the number of bits communicated between Alice and Bob in the worst case.

The problem of checking identity is formally defined by the function EQ as follows: [math]\displaystyle{ \mathrm{EQ}:\{0,1\}^n\times\{0,1\}^n\rightarrow\{0,1\} }[/math] and for any [math]\displaystyle{ a,b\in\{0,1\}^n }[/math],

[math]\displaystyle{ \mathrm{EQ}(a,b)= \begin{cases} 1& \mbox{if } a=b,\\ 0& \mbox{otherwise.} \end{cases} }[/math]

A trivial way to solve EQ is to let Bob send his entire input string [math]\displaystyle{ b }[/math] to Alice and let Alice check whether [math]\displaystyle{ a=b }[/math]. This costs [math]\displaystyle{ n }[/math] bits of communications.

It is known that for deterministic communication protocols, this is the best we can get for computing EQ.

Theorem (Yao 1979)

Any deterministic communication protocol computing EQ on two [math]\displaystyle{ n }[/math]-bit strings costs [math]\displaystyle{ n }[/math] bits of communication in the worst-case.

This theorem is much more nontrivial to prove than it looks, because Alice and Bob are allowed to interact with each other in arbitrary ways. The proof of this theorem in Yao's 1979 paper initiates the field of communication complexity.

If the randomness is allowed, we can solve this problem up to a tolerable probabilistic error with significantly less communications. The inputs [math]\displaystyle{ a,b\in\{0,1\}^{n} }[/math] are two strings [math]\displaystyle{ a=a_0a_1\cdots a_{n-1}, b=b_0b_1\cdots b_{n-1} }[/math] of [math]\displaystyle{ n }[/math] bits. Let [math]\displaystyle{ k=\lceil\log_2 (2n)\rceil }[/math] and [math]\displaystyle{ p\in[2^k,2^{k+1}] }[/math] be an arbitrary prime number. (Such a prime [math]\displaystyle{ p }[/math] always exists.) The input strings [math]\displaystyle{ a,b }[/math] can be respectively represented as two polynomials [math]\displaystyle{ f,g\in\mathbb{Z}_p[x] }[/math] such that [math]\displaystyle{ f(x)=\sum_{i=0}^{n-1}a_ix^{i} }[/math] and [math]\displaystyle{ g(x)=\sum_{i=0}^{n-1}b_ix^{i} }[/math] of degree [math]\displaystyle{ n-1 }[/math], where all additions and multiplications are modulo [math]\displaystyle{ p }[/math]. The randomized communication protocol is given as follows:

A randomized protocol for EQ

Alice does: pick [math]\displaystyle{ x\in[p] }[/math] uniformly at random; send [math]\displaystyle{ x }[/math] and [math]\displaystyle{ f(x) }[/math] to Bob; Upon receiving [math]\displaystyle{ x }[/math] and [math]\displaystyle{ f(x) }[/math] Bob does: If [math]\displaystyle{ f(x)= g(x) }[/math] return "yes"; else return "no".

Repeat this protocol for 100 times. The total number of bits to communicate is bounded by [math]\displaystyle{ 200\log_2p=O(\log n) }[/math]. Due to the analysis of the randomized algorithm for PIT, if [math]\displaystyle{ a=b }[/math] the protocol is always correct and if [math]\displaystyle{ a\neq b }[/math] the protocol fails to report a difference with probability less than [math]\displaystyle{ 2^{-100} }[/math].