Randomized Algorithms (Spring 2010)/Balls and bins
Today's materiels are the common senses for randomized algorithms.
Probability Basics
In probability theory class we have learned the basic concepts of events and random variables. The following are some examples:
event [math]\displaystyle{ \mathcal{E} }[/math]: random variable [math]\displaystyle{ X }[/math]: [math]\displaystyle{ \mathcal{E}_1 }[/math]: 75 out of 100 coin flips are HEADs [math]\displaystyle{ X_1 }[/math] is the number of HEADs in the 100 coin flips [math]\displaystyle{ \mathcal{E}_2 }[/math]: the result of rolling a 6-sided die is an even number (2, 4, 6) [math]\displaystyle{ X_2 }[/math] is the result of rolling a die [math]\displaystyle{ \mathcal{E}_3 }[/math]: tomorrow is rainy [math]\displaystyle{ X_3=1 }[/math] if tomorrow is rainy and [math]\displaystyle{ X_3=0 }[/math] if otherwise
Events and random variables can be related:
- An event can be defined from random variables [math]\displaystyle{ X, Y }[/math] by a predicate [math]\displaystyle{ P(X, Y) }[/math]. ([math]\displaystyle{ \mathcal{E} }[/math]: X>Y)
- A boolean random variable [math]\displaystyle{ X }[/math] can be defined from an event [math]\displaystyle{ \mathcal{E} }[/math] as follows:
- [math]\displaystyle{ \begin{align}X=\begin{cases}1& \mathcal{E} \text{ occurs}\\ 0& \text{ otherwise}\end{cases}\end{align} }[/math]
We say that [math]\displaystyle{ X }[/math] indicates the event [math]\displaystyle{ \mathcal{E} }[/math]. We will later see that this indicator trick is very useful for probabilistic analysis.
The formal definitions of events and random variables are related to the foundation of probability theory, which is not the topic of this class. Here we only give an informal description (you may ignore them if you feel confused):
- A probability space is a set [math]\displaystyle{ \Omega }[/math] of elementary events, also called samples. (6 sides of a die)
- An event is a subset of [math]\displaystyle{ \Omega }[/math], i.e. a set of elementary events. ([math]\displaystyle{ \mathcal{E}_2 }[/math]: side 2, 4, 6 of the die)
- A random variable is not really a variable, but a function! The function maps events to values. ([math]\displaystyle{ X_2 }[/math] maps the first side of the die to 1, the second side to 2, the third side to 3, ...)
The axiom foundation of probability theory is laid by Kolmogorov, one of the greatest mathematician of the 20th century, who advanced various very different fields of mathematics.
Independent events
Definition (Independent events) - Two events [math]\displaystyle{ \mathcal{E}_1 }[/math] and [math]\displaystyle{ \mathcal{E}_2 }[/math] are independent if and only if
- [math]\displaystyle{ \begin{align} \Pr\left[\mathcal{E}_1 \wedge \mathcal{E}_2\right] &= \Pr[\mathcal{E}_1]\cdot\Pr[\mathcal{E}_2]. \end{align} }[/math]
- Two events [math]\displaystyle{ \mathcal{E}_1 }[/math] and [math]\displaystyle{ \mathcal{E}_2 }[/math] are independent if and only if
This definition can be generalized to any number of events:
Definition (Independent events) - Events [math]\displaystyle{ \mathcal{E}_1, \mathcal{E}_2, \ldots, \mathcal{E}_n }[/math] are mutually independent if and only if, for any subset [math]\displaystyle{ I\subseteq\{1,2,\ldots,n\} }[/math],
- [math]\displaystyle{ \begin{align} \Pr\left[\bigwedge_{i\in I}\mathcal{E}_i\right] &= \prod_{i\in I}\Pr[\mathcal{E}_i]. \end{align} }[/math]
- Events [math]\displaystyle{ \mathcal{E}_1, \mathcal{E}_2, \ldots, \mathcal{E}_n }[/math] are mutually independent if and only if, for any subset [math]\displaystyle{ I\subseteq\{1,2,\ldots,n\} }[/math],
The independence can also be defined for variables:
Definition (Independent variables) - Two random variables [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] are independent if and only if
- [math]\displaystyle{ \Pr[(X=x)\wedge(Y=y)]=\Pr[X=x]\cdot\Pr[Y=y] }[/math]
- for all values [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math]. Random variables [math]\displaystyle{ X_1, X_2, \ldots, X_n }[/math] are mutually independent if and only if, for any subset [math]\displaystyle{ I\subseteq\{1,2,\ldots,n\} }[/math] and any values [math]\displaystyle{ x_i }[/math], where [math]\displaystyle{ i\in I }[/math],
- [math]\displaystyle{ \begin{align} \Pr\left[\bigwedge_{i\in I}(X_i=x_i)\right] &= \prod_{i\in I}\Pr[X_i=x_i]. \end{align} }[/math]
- Two random variables [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] are independent if and only if
Note that in probability theory, the "mutual independence" is not equivalent with "pair-wise independence", which we will learn in the future.
The union bound
We are familiar with the principle of inclusion-exclusion for finite sets.
Principle of Inclusion-Exclusion - Let [math]\displaystyle{ S_1, S_2, \ldots, S_n }[/math] be [math]\displaystyle{ n }[/math] finite sets. Then
- [math]\displaystyle{ \begin{align} \left|\bigcup_{1\le i\le n}S_i\right| &= \sum_{i=1}^n|S_i| -\sum_{i\lt j}|S_i\cap S_j| +\sum_{i\lt j\lt k}|S_i\cap S_j\cap S_k|\\ & \quad -\cdots +(-1)^{\ell-1}\sum_{i_1\lt i_2\lt \cdots\lt i_\ell}\left|\bigcap_{r=1}^\ell S_{i_r}\right| +\cdots +(-1)^{n-1} \left|\bigcap_{i=1}^n S_i\right|. \end{align} }[/math]
- Let [math]\displaystyle{ S_1, S_2, \ldots, S_n }[/math] be [math]\displaystyle{ n }[/math] finite sets. Then
The principle can be generalized to probability events.
Principle of Inclusion-Exclusion - Let [math]\displaystyle{ \mathcal{E}_1, \mathcal{E}_2, \ldots, \mathcal{E}_n }[/math] be [math]\displaystyle{ n }[/math] events. Then
- [math]\displaystyle{ \begin{align} \Pr\left[\bigvee_{1\le i\le n}\mathcal{E}_i\right] &= \sum_{i=1}^n\Pr[\mathcal{E}_i] -\sum_{i\lt j}\Pr[\mathcal{E}_i\wedge \mathcal{E}_j] +\sum_{i\lt j\lt k}\Pr[\mathcal{E}_i\wedge \mathcal{E}_j\wedge \mathcal{E}_k]\\ & \quad -\cdots +(-1)^{\ell-1}\sum_{i_1\lt i_2\lt \cdots\lt i_\ell}\Pr\left[\bigwedge_{r=1}^\ell \mathcal{E}_{i_r}\right] +\cdots +(-1)^{n-1}\Pr\left[\bigwedge_{i=1}^n \mathcal{E}_{i}\right]. \end{align} }[/math]
- Let [math]\displaystyle{ \mathcal{E}_1, \mathcal{E}_2, \ldots, \mathcal{E}_n }[/math] be [math]\displaystyle{ n }[/math] events. Then
The principle is implied by the axiomatic formalization of probability. The following inequality is implied (nontrivially) by the principle of inclusion-exclusion:
Theorem (the union bound) - Let [math]\displaystyle{ \mathcal{E}_1, \mathcal{E}_2, \ldots, \mathcal{E}_n }[/math] be [math]\displaystyle{ n }[/math] events. Then
- [math]\displaystyle{ \begin{align} \Pr\left[\bigvee_{1\le i\le n}\mathcal{E}_i\right] &\le \sum_{i=1}^n\Pr[\mathcal{E}_i]. \end{align} }[/math]
- Let [math]\displaystyle{ \mathcal{E}_1, \mathcal{E}_2, \ldots, \mathcal{E}_n }[/math] be [math]\displaystyle{ n }[/math] events. Then
The name of this inequality is Boole's inequality. It is usually referred by its nickname "the union bound". The bound holds for arbitrary events, even if they are dependent. Due to this generality, the union bound is extremely useful for analyzing the union of events.
Linearity of expectation
Let [math]\displaystyle{ X }[/math] be a discrete random variable. The expectation of [math]\displaystyle{ X }[/math] is defined as follows.
Definition (Expectation) - The expectation of a discrete random variable [math]\displaystyle{ X }[/math], denoted by [math]\displaystyle{ \mathbf{E}[X] }[/math], is given by
- [math]\displaystyle{ \begin{align} \mathbf{E}[X] &= \sum_{x}x\Pr[X=x], \end{align} }[/math]
- where the summation is over all values [math]\displaystyle{ x }[/math] in the range of [math]\displaystyle{ X }[/math].
- The expectation of a discrete random variable [math]\displaystyle{ X }[/math], denoted by [math]\displaystyle{ \mathbf{E}[X] }[/math], is given by
Perhaps the most useful property of expectation is its linearity.
Theorem (Linearity of Expectations) - For any discrete random variables [math]\displaystyle{ X_1, X_2, \ldots, X_n }[/math], and any real constants [math]\displaystyle{ a_1, a_2, \ldots, a_n }[/math],
- [math]\displaystyle{ \begin{align} \mathbf{E}\left[\sum_{i=1}^n a_iX_i\right] &= \sum_{i=1}^n a_i\cdot\mathbf{E}[X_i]. \end{align} }[/math]
- For any discrete random variables [math]\displaystyle{ X_1, X_2, \ldots, X_n }[/math], and any real constants [math]\displaystyle{ a_1, a_2, \ldots, a_n }[/math],
Proof. By the definition of the expectations, it is easy to verify that (try to prove by yourself): for any discrete random variables [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math], and any real constant [math]\displaystyle{ c }[/math],
- [math]\displaystyle{ \mathbf{E}[X+Y]=\mathbf{E}[X]+\mathbf{E}[Y] }[/math];
- [math]\displaystyle{ \mathbf{E}[cX]=c\mathbf{E}[X] }[/math].
The theorem follows by induction.
- [math]\displaystyle{ \square }[/math]
Example - Supposed that we have a biased coin that the probability of HEADs is [math]\displaystyle{ p }[/math]. Flipping the coin for n times, what is the expectation of number of HEADs?
- It looks straightforward that it must be np, but how can we prove it? Surely we can apply the definition of expectation to compute the expectation with brute force. A more convenient way is by the linearity of expectations: Let [math]\displaystyle{ X_i }[/math] indicate whether the [math]\displaystyle{ i }[/math]-th flip is HEADs. Then [math]\displaystyle{ \mathbf{E}[X_i]=1\cdot p+0\cdot(1-p)=p }[/math], and the total number of HEADs after n flips is [math]\displaystyle{ X=\sum_{i=1}^{n}X_i }[/math]. Applying the linearity of expectation, the expected number of HEADs is:
- [math]\displaystyle{ \mathbf{E}[X]=\mathbf{E}\left[\sum_{i=1}^{n}X_i\right]=\sum_{i=1}^{n}\mathbf{E}[X_i]=np }[/math].
The real power of the linearity of expectations is that it does not require the random variables to be independent, thus can be applied to any set of random variables. For example:
- [math]\displaystyle{ \mathbf{E}\left[\alpha X+\beta X^2+\gamma X^3\right] = \alpha\cdot\mathbf{E}[X]+\beta\cdot\mathbf{E}\left[X^2\right]+\gamma\cdot\mathbf{E}\left[X^3\right]. }[/math]
However, do not exaggerate this power!
- For an arbitrary function [math]\displaystyle{ f }[/math] (not necessarily linear), the equation [math]\displaystyle{ \mathbf{E}[f(X)]=f(\mathbf{E}[X]) }[/math] does not hold generally.
- For variances, the equation [math]\displaystyle{ var(X+Y)=var(X)+var(Y) }[/math] does not hold without further assumption of the independence of [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math].
Law of total probability(expectation)
In probability theory, the word "condition" is a verb. "Conditioning on the event ..." means that it is assumed that the event occurs.
Definition (conditional probability) - The conditional probability that event [math]\displaystyle{ \mathcal{E}_1 }[/math] occurs given that event [math]\displaystyle{ \mathcal{E}_2 }[/math] occurs is
- [math]\displaystyle{ \Pr[\mathcal{E}_1\mid \mathcal{E}_2]=\frac{\Pr[\mathcal{E}_1\wedge \mathcal{E}_2]}{\Pr[\mathcal{E}_2]}. }[/math]
- The conditional probability that event [math]\displaystyle{ \mathcal{E}_1 }[/math] occurs given that event [math]\displaystyle{ \mathcal{E}_2 }[/math] occurs is
The conditional probability is well-defined only if [math]\displaystyle{ \Pr[\mathcal{E}_2]\neq0 }[/math].
For independent events [math]\displaystyle{ \mathcal{E}_1 }[/math] and [math]\displaystyle{ \mathcal{E}_2 }[/math], it holds that
- [math]\displaystyle{ \Pr[\mathcal{E}_1\mid \mathcal{E}_2]=\frac{\Pr[\mathcal{E}_1\wedge \mathcal{E}_2]}{\Pr[\mathcal{E}_2]} =\frac{\Pr[\mathcal{E}_1]\cdot\Pr[\mathcal{E}_2]}{\Pr[\mathcal{E}_2]} =\Pr[\mathcal{E}_1]. }[/math]
It supports our intuition that for two independent events, whether one of them occurs will not affect the chance of the other.
The following fact is known as the law of total probability. It computes the probability by averaging over all possible cases.
Theorem (law of total probability) - Let [math]\displaystyle{ \mathcal{E}_1,\mathcal{E}_2,\ldots,\mathcal{E}_n }[/math] be mutually disjoint events, and [math]\displaystyle{ \bigvee_{i=1}^n\mathcal{E}_i=\Omega }[/math] is the sample space.
- Then for any event [math]\displaystyle{ \mathcal{E} }[/math],
- [math]\displaystyle{ \Pr[\mathcal{E}]=\sum_{i=1}^n\Pr[\mathcal{E}\mid\mathcal{E}_i]\cdot\Pr[\mathcal{E}_i]. }[/math]
Proof. Since [math]\displaystyle{ \mathcal{E}_1,\mathcal{E}_2,\ldots,\mathcal{E}_n }[/math] are mutually disjoint and [math]\displaystyle{ \bigvee_{i=1}^n\mathcal{E}_i=\Omega }[/math], events [math]\displaystyle{ \mathcal{E}\wedge\mathcal{E}_1,\mathcal{E}\wedge\mathcal{E}_2,\ldots,\mathcal{E}\wedge\mathcal{E}_n }[/math] are also mutually disjoint, and [math]\displaystyle{ \mathcal{E}=\bigvee_{i=1}^n\left(\mathcal{E}\wedge\mathcal{E}_i\right) }[/math]. Then - [math]\displaystyle{ \Pr[\mathcal{E}]=\sum_{i=1}^n\Pr[\mathcal{E}\wedge\mathcal{E}_i], }[/math]
which according to the definition of conditional probability, is [math]\displaystyle{ \sum_{i=1}^n\Pr[\mathcal{E}\mid\mathcal{E}_i]\cdot\Pr[\mathcal{E}_i] }[/math].
- [math]\displaystyle{ \square }[/math]
Conditional expectation can be accordingly defined:
Definition (conditional expectation) - For random variables [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math],
- [math]\displaystyle{ \mathbf{E}[X\mid Y=y]=\sum_{x}x\Pr[X=x\mid Y=y], }[/math]
- where the summation is taken over the range of [math]\displaystyle{ X }[/math].
- For random variables [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math],
There is also a law of total expectation.
Theorem (law of total expectation) - Let [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] be two random variables. Then
- [math]\displaystyle{ \mathbf{E}[X]=\sum_{y}\mathbf{E}[X\mid Y=y]\cdot\Pr[Y=y]. }[/math]
- Let [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] be two random variables. Then
The law of total probability (expectation) provides us a standard tool for breaking a probability (or an expectation) into sub-cases. Sometimes, it helps the analysis.
Distributions of coin flips
We introduce several important distributions induced by independent coin flips (independent probabilistic experiments), including: Bernoulli trial, geometric distribution, binomial distribution.
- Bernoulli trial (Bernoulli distribution)
- Bernoulli trial describes the probability distribution of a single (biased) coin flip. Suppose that we flip a (biased) coin where the probability of HEADS is [math]\displaystyle{ p }[/math]. Let [math]\displaystyle{ X }[/math] be the 0-1 random variable which indicates whether the result is HEADS. We say that [math]\displaystyle{ X }[/math] follows the Bernoulli distribution with parameter [math]\displaystyle{ p }[/math]. Formally,
- [math]\displaystyle{ \begin{align} X &= \begin{cases} 1 & \text{with probability }p\\ 0 & \text{with probability }1-p \end{cases} \end{align} }[/math].
- Geometric distribution
- Suppose we flip the same coin repeatedly until HEADS appears, where each coin flip is independent and follows the Bernoulli distribution with parameter [math]\displaystyle{ p }[/math]. Let [math]\displaystyle{ X }[/math] be the random variable denoting the total number of coin flips. Then [math]\displaystyle{ X }[/math] has the geometric distribution with parameter [math]\displaystyle{ p }[/math]. Formally, [math]\displaystyle{ \Pr[X=k]=(1-p)^{k-1}p }[/math].
- For geometric [math]\displaystyle{ X }[/math], [math]\displaystyle{ \mathbf{E}[X]=\frac{1}{p} }[/math]. This can be verified by directly computing [math]\displaystyle{ \mathbf{E}[X] }[/math] by the definition of expectations. There is also a smarter way of computing [math]\displaystyle{ \mathbf{E}[X] }[/math], by using indicators and the linearity of expectations. For [math]\displaystyle{ k=0, 1, 2, \ldots }[/math], let [math]\displaystyle{ Y_k }[/math] be the 0-1 random variable such that [math]\displaystyle{ Y_k=1 }[/math] if and only if none of the first [math]\displaystyle{ k }[/math] coin flipings are HEADS, thus [math]\displaystyle{ \mathbf{E}[Y_k]=\Pr[Y_k=1]=(1-p)^{k} }[/math]. A key observation is that [math]\displaystyle{ X=\sum_{k=0}^\infty Y_k }[/math]. Thus, due to the linearity of expectations,
- [math]\displaystyle{ \begin{align} \mathbf{E}[X] = \mathbf{E}\left[\sum_{k=0}^\infty Y_k\right] = \sum_{k=0}^\infty \mathbf{E}[Y_k] = \sum_{k=0}^\infty (1-p)^k = \frac{1}{1-(1-p)} =\frac{1}{p}. \end{align} }[/math]
- Binomial distribution
- Suppose we flip the same (biased) coin for [math]\displaystyle{ n }[/math] times, where each coin flip is independent and follows the Bernoulli distribution with parameter [math]\displaystyle{ p }[/math]. Let [math]\displaystyle{ X }[/math] be the number of HEADS. Then [math]\displaystyle{ X }[/math] has the binomial distribution with parameters [math]\displaystyle{ n }[/math] and [math]\displaystyle{ p }[/math]. Formally, [math]\displaystyle{ \Pr[X=k]={n\choose k}p^k(1-p)^{n-k} }[/math].
- A binomial random variable [math]\displaystyle{ X }[/math] with parameters [math]\displaystyle{ n }[/math] and [math]\displaystyle{ p }[/math] is usually denoted by [math]\displaystyle{ B(n,p) }[/math].
- As we saw above, by applying the linearity of expectations, it is easy to show that [math]\displaystyle{ \mathbf{E}[X]=np }[/math] for an [math]\displaystyle{ X=B(n,p) }[/math].
Balls-into-bins model
Imagine that [math]\displaystyle{ m }[/math] balls are thrown into [math]\displaystyle{ n }[/math] bins, in such a way that each ball is thrown into a bin which is uniformly and independently chosen from all [math]\displaystyle{ n }[/math] bins.
There are several information we would like to know about this random process. For example:
- the probability that there is no bin with more than one balls (the birthday problem)
- the number of balls thrown to make sure there is no empty bins (coupon collector problem)
- the distribution of the loads of bins (occupancy problem)
Why is this model useful anyway? It is useful because it is not just about throwing balls into bins, but a uniformly random function mapping [math]\displaystyle{ [m] }[/math] to [math]\displaystyle{ [n] }[/math]. So we are actually looking at the behaviors of random mappings.
Birthday paradox
There are [math]\displaystyle{ m }[/math] students in the class. Assume that for each student, his/her birthday is uniformly and independently distributed over the 365 days in a years. We wonder what the probability that no two students share a birthday.
Due to the pigeonhole principle, it is obvious that for [math]\displaystyle{ m\gt 365 }[/math], there must be two students with the same birthday. Surprisingly, for any [math]\displaystyle{ m\gt 57 }[/math] this event occurs with more than 99% probability. This is called the birthday paradox. Despite the name, the birthday paradox is not a real paradox.
We can model this problem as a balls-into-bins problem. [math]\displaystyle{ m }[/math] different balls (students) are uniformly and independently thrown into 365 bins (days). More generally, let [math]\displaystyle{ n }[/math] be the number of bins. We ask for the probability of the following event [math]\displaystyle{ \mathcal{E} }[/math]
- [math]\displaystyle{ \mathcal{E} }[/math]: there is no bin with more than one balls (i.e. no two students share birthday).
We first analyze this by counting. There are totally [math]\displaystyle{ n^m }[/math] ways of assigning [math]\displaystyle{ m }[/math] balls to [math]\displaystyle{ n }[/math] bins. The number of assignments that no two balls share a bin is [math]\displaystyle{ {n\choose m}m! }[/math].
Thus the probability is given by:
- [math]\displaystyle{ \begin{align} \Pr[\mathcal{E}] = \frac{{n\choose m}m!}{n^m}. \end{align} }[/math]
Recall that [math]\displaystyle{ {n\choose m}=\frac{n!}{(n-m)!m!} }[/math]. Then
- [math]\displaystyle{ \begin{align} \Pr[\mathcal{E}] = \frac{{n\choose m}m!}{n^m} = \frac{n!}{n^m(n-m)!} = \frac{n}{n}\cdot\frac{n-1}{n}\cdot\frac{n-2}{n}\cdots\frac{n-(m-1)}{n} = \prod_{k=1}^{m-1}\left(1-\frac{k}{n}\right). \end{align} }[/math]
There is also a more "probabilistic" argument for the above equation. To be rigorous, we need the following theorem, which holds generally and is very useful for computing the AND of many events.
By the definition of conditional probability, [math]\displaystyle{ \Pr[A\mid B]=\frac{\Pr[A\wedge B]}{\Pr[B]} }[/math]. Thus, [math]\displaystyle{ \Pr[A\wedge B] =\Pr[B]\cdot\Pr[A\mid B] }[/math]. This hints us that we can compute the probability of the AND of events by conditional probabilities. Formally, we have the following theorem: Theorem:
- Let [math]\displaystyle{ \mathcal{E}_1, \mathcal{E}_2, \ldots, \mathcal{E}_n }[/math] be any [math]\displaystyle{ n }[/math] events. Then
- [math]\displaystyle{ \begin{align} \Pr\left[\bigwedge_{i=1}^n\mathcal{E}_i\right] &= \prod_{k=1}^n\Pr\left[\mathcal{E}_k \mid \bigwedge_{i\lt k}\mathcal{E}_i\right]. \end{align} }[/math]
Proof: It holds that [math]\displaystyle{ \Pr[A\wedge B] =\Pr[B]\cdot\Pr[A\mid B] }[/math]. Thus, let [math]\displaystyle{ A=\mathcal{E}_n }[/math] and [math]\displaystyle{ B=\mathcal{E}_1\wedge\mathcal{E}_2\wedge\cdots\wedge\mathcal{E}_{n-1} }[/math], then
- [math]\displaystyle{ \begin{align} \Pr[\mathcal{E}_1\wedge\mathcal{E}_2\wedge\cdots\wedge\mathcal{E}_n] &= \Pr[\mathcal{E}_1\wedge\mathcal{E}_2\wedge\cdots\wedge\mathcal{E}_{n-1}]\cdot\Pr\left[\mathcal{E}_n\mid \bigwedge_{i\lt n}\mathcal{E}_i\right]. \end{align} }[/math]
Recursively applying this equation to [math]\displaystyle{ \Pr[\mathcal{E}_1\wedge\mathcal{E}_2\wedge\cdots\wedge\mathcal{E}_{n-1}] }[/math] until there is only [math]\displaystyle{ \mathcal{E}_1 }[/math] left, the theorem is proved. [math]\displaystyle{ \square }[/math]
- Let [math]\displaystyle{ \mathcal{E}_1, \mathcal{E}_2, \ldots, \mathcal{E}_n }[/math] be any [math]\displaystyle{ n }[/math] events. Then
Now we are back to the probabilistic analysis of the birthday problem, with a general setting of [math]\displaystyle{ m }[/math] students and [math]\displaystyle{ n }[/math] possible birthdays (imagine that we live in a planet where a year has [math]\displaystyle{ n }[/math] days).
The first student has a birthday (of course!). The probability that the second student has a different birthday is [math]\displaystyle{ \left(1-\frac{1}{n}\right) }[/math]. Given that the first two students have different birthdays, the probability that the third student has a different birthday from the first two is [math]\displaystyle{ \left(1-\frac{2}{n}\right) }[/math]. Continuing this on, assuming that the first [math]\displaystyle{ k-1 }[/math] students all have different birthdays, the probability that the [math]\displaystyle{ k }[/math]th student has a different birthday than the first [math]\displaystyle{ k-1 }[/math], is given by [math]\displaystyle{ \left(1-\frac{k-1}{n}\right) }[/math]. So the probability that all [math]\displaystyle{ m }[/math] students have different birthdays is the product of all these conditional probabilities:
- [math]\displaystyle{ \begin{align} \Pr[\mathcal{E}]=\left(1-\frac{1}{n}\right)\cdot \left(1-\frac{2}{n}\right)\cdots \left(1-\frac{m-1}{n}\right) &= \prod_{k=1}^{m-1}\left(1-\frac{k}{n}\right), \end{align} }[/math]
which is the same as what we got by the counting argument.
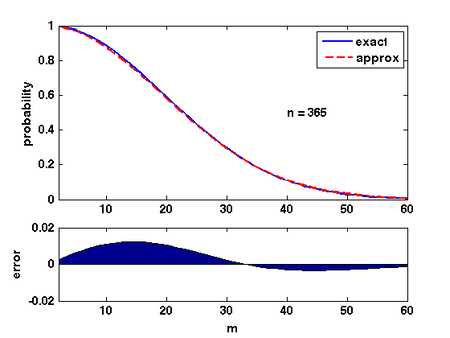
There are several ways of analyzing this formular. Here is a convenient one: Due to Taylor's expansion, [math]\displaystyle{ e^{-k/n}\approx 1-k/n }[/math]. Then
- [math]\displaystyle{ \begin{align} \prod_{k=1}^{m-1}\left(1-\frac{k}{n}\right) &\approx \prod_{k=1}^{m-1}e^{-\frac{k}{n}}\\ &= \exp\left(-\sum_{k=1}^{m-1}\frac{k}{n}\right)\\ &= e^{-m(m-1)/2n}\\ &\approx e^{-m^2/2n}. \end{align} }[/math]
The quality of this approximation is shown in the Figure.
Therefore, for [math]\displaystyle{ m=\sqrt{2n\ln \frac{1}{\epsilon}} }[/math], the probability that [math]\displaystyle{ \Pr[\mathcal{E}]\approx\epsilon }[/math].
Coupon collector's problem
Suppose that a chocolate company releases [math]\displaystyle{ n }[/math] different types of coupons. Each box of chocolates contains one coupon with a uniformly random type. Once you have collected all [math]\displaystyle{ n }[/math] types of coupons, you will get a prize. So how many boxes of chocolates you are expected to buy to win the prize?
The coupon collector problem can be described in the balls-into-bins model as follows. We keep throwing balls one-by-one into [math]\displaystyle{ n }[/math] bins (coupons), such that each ball is thrown into a bin uniformly and independently at random. Each ball corresponds to a box of chocolate, and each bin corresponds to a type of coupon. Thus, the number of boxes bought to collect [math]\displaystyle{ n }[/math] coupons is just the number of balls thrown until none of the [math]\displaystyle{ n }[/math] bins is empty.
Theorem - Let [math]\displaystyle{ X }[/math] be the number of balls thrown uniformly and independently to [math]\displaystyle{ n }[/math] bins until no bin is empty. Then [math]\displaystyle{ \mathbf{E}[X]=nH(n) }[/math], where [math]\displaystyle{ H(n) }[/math] is the [math]\displaystyle{ n }[/math]th harmonic number.
Proof. Let [math]\displaystyle{ X_i }[/math] be the number of balls thrown while there are exactly [math]\displaystyle{ i-1 }[/math] nonempty bins, then clearly [math]\displaystyle{ X=\sum_{i=1}^n X_i }[/math]. When there are exactly [math]\displaystyle{ i-1 }[/math] nonempty bins, throwing a ball, the probability that the number of nonempty bins increases (i.e. the ball is thrown to an empty bin) is
- [math]\displaystyle{ p_i=1-\frac{i-1}{n}. }[/math]
[math]\displaystyle{ X_i }[/math] is the number of balls thrown to make the number of nonempty bins increases from [math]\displaystyle{ i-1 }[/math] to [math]\displaystyle{ i }[/math], i.e. the number of balls thrown until a ball is thrown to a current empty bin. Thus, [math]\displaystyle{ X_i }[/math] follows the geometric distribution, such that
- [math]\displaystyle{ \Pr[X_i=k]=(1-p_i)^{k-1}p_i }[/math]
For a geometric random variable, [math]\displaystyle{ \mathbf{E}[X_i]=\frac{1}{p_i}=\frac{n}{n-i+1} }[/math].
Applying the linearity of expectations,
- [math]\displaystyle{ \begin{align} \mathbf{E}[X] &= \mathbf{E}\left[\sum_{i=1}^nX_i\right]\\ &= \sum_{i=1}^n\mathbf{E}\left[X_i\right]\\ &= \sum_{i=1}^n\frac{n}{n-i+1}\\ &= n\sum_{i=1}^n\frac{1}{i}\\ &= nH(n), \end{align} }[/math]
where [math]\displaystyle{ H(n) }[/math] is the [math]\displaystyle{ n }[/math]th Harmonic number, and [math]\displaystyle{ H(n)=\ln n+O(1) }[/math]. Thus, for the coupon collectors problem, the expected number of coupons required to obtain all [math]\displaystyle{ n }[/math] types of coupons is [math]\displaystyle{ n\ln n+O(n) }[/math].
- [math]\displaystyle{ \square }[/math]
Only knowing the expectation is not good enough. We would like to know how fast the probability decrease as a random variable deviates from its mean value.
Theorem - Let [math]\displaystyle{ X }[/math] be the number of balls thrown uniformly and independently to [math]\displaystyle{ n }[/math] bins until no bin is empty. Then [math]\displaystyle{ \Pr[X\ge n\ln n+cn]\lt e^{-c} }[/math] for any [math]\displaystyle{ c\gt 0 }[/math].
Proof. For any particular bin [math]\displaystyle{ i }[/math], the probability that bin [math]\displaystyle{ i }[/math] is empty after throwing [math]\displaystyle{ n\ln n+cn }[/math] balls is - [math]\displaystyle{ \left(1-\frac{1}{n}\right)^{n\ln n+cn} \lt e^{-(\ln n+c)} =\frac{1}{ne^c}. }[/math]
By the union bound, the probability that there exists an empty bin after throwing [math]\displaystyle{ n\ln n+cn }[/math] balls is
- [math]\displaystyle{ \Pr[X\ge n\ln n+cn] \lt n\cdot \frac{1}{ne^c} =e^{-c}. }[/math]
- [math]\displaystyle{ \square }[/math]
Occupancy problem
Now we ask about the loads of bins. Assuming that [math]\displaystyle{ m }[/math] balls are uniformly and independently assigned to [math]\displaystyle{ n }[/math] bins, for [math]\displaystyle{ 1\le i\le n }[/math], let [math]\displaystyle{ X_i }[/math] be the load of the [math]\displaystyle{ i }[/math]th bin, i.e. the number of balls in the [math]\displaystyle{ i }[/math]th bin.
An easy analysis shows that for every bin [math]\displaystyle{ i }[/math], the expected load [math]\displaystyle{ \mathbf{E}[X_i] }[/math] is equal to the average load [math]\displaystyle{ m/n }[/math].
Because there are totally [math]\displaystyle{ m }[/math] balls, it is always true that [math]\displaystyle{ \sum_{i=1}^n X_i=m }[/math].
Therefore, due to the linearity of expectations,
- [math]\displaystyle{ \begin{align} \sum_{i=1}^n\mathbf{E}[X_i] &= \mathbf{E}\left[\sum_{i=1}^n X_i\right] = \mathbf{E}\left[m\right] =m. \end{align} }[/math]
Because for each ball, the bin to which the ball is assigned is uniformly and independently chosen, the distributions of the loads of bins are identical. Thus [math]\displaystyle{ \mathbf{E}[X_i] }[/math] is the same for each [math]\displaystyle{ i }[/math]. Combining with the above equation, it holds that for every [math]\displaystyle{ 1\le i\le m }[/math], [math]\displaystyle{ \mathbf{E}[X_i]=\frac{m}{n} }[/math]. So the average is indeed the average!
Next we analyze the distribution of the maximum load. We show that when [math]\displaystyle{ m=n }[/math], i.e. [math]\displaystyle{ n }[/math] balls are uniformly and independently thrown into [math]\displaystyle{ n }[/math] bins, the maximum load is [math]\displaystyle{ O\left(\frac{\log n}{\log\log n}\right) }[/math] with high probability.
Theorem - Suppose that [math]\displaystyle{ n }[/math] balls are thrown independently and uniformly at random into [math]\displaystyle{ n }[/math] bins. For [math]\displaystyle{ 1\le i\le n }[/math], let [math]\displaystyle{ X_i }[/math] be the random variable denoting the number of balls in the [math]\displaystyle{ i }[/math]th bin. Then
- [math]\displaystyle{ \Pr\left[\max_{1\le i\le n}X_i \ge\frac{3\ln n}{\ln\ln n}\right] \lt \frac{1}{n}. }[/math]
- Suppose that [math]\displaystyle{ n }[/math] balls are thrown independently and uniformly at random into [math]\displaystyle{ n }[/math] bins. For [math]\displaystyle{ 1\le i\le n }[/math], let [math]\displaystyle{ X_i }[/math] be the random variable denoting the number of balls in the [math]\displaystyle{ i }[/math]th bin. Then
Proof. Let [math]\displaystyle{ M }[/math] be an integer. Take bin 1. For any particular [math]\displaystyle{ M }[/math] balls, these [math]\displaystyle{ M }[/math] balls are all thrown to bin 1 with probability [math]\displaystyle{ (1/n)^M }[/math], and there are totally [math]\displaystyle{ {n\choose M} }[/math] distinct sets of [math]\displaystyle{ M }[/math] balls. Therefore, applying the union bound, - [math]\displaystyle{ \begin{align}\Pr\left[X_1\ge M\right] &\le {n\choose M}\left(\frac{1}{n}\right)^M\\ &= \frac{n!}{M!(n-M)!n^M}\\ &= \frac{1}{M!}\cdot\frac{n(n-1)(n-2)\cdots(n-M+1)}{n^M}\\ &= \frac{1}{M!}\cdot \prod_{i=0}^{M-1}\left(1-\frac{i}{n}\right)\\ &\le \frac{1}{M!}. \end{align} }[/math]
According to Stirling's approximation, [math]\displaystyle{ M!\approx \sqrt{2\pi M}\left(\frac{M}{e}\right)^M }[/math], thus
- [math]\displaystyle{ \frac{1}{M!}\le\left(\frac{e}{M}\right)^M. }[/math]
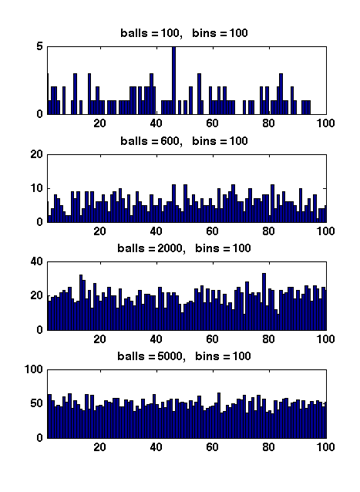
Figure 1 Due to the symmetry. All [math]\displaystyle{ X_i }[/math] have the same distribution. Apply the union bound again,
- [math]\displaystyle{ \begin{align} \Pr\left[\max_{1\le i\le n}X_i\ge M\right] &= \Pr\left[(X_1\ge M) \vee (X_2\ge M) \vee\cdots\vee (X_n\ge M)\right]\\ &\le n\Pr[X_1\ge M]\\ &\le n\left(\frac{e}{M}\right)^M. \end{align} }[/math]
When [math]\displaystyle{ M=3\ln n/\ln\ln n }[/math],
- [math]\displaystyle{ \begin{align} \left(\frac{e}{M}\right)^M &= \left(\frac{e\ln\ln n}{3\ln n}\right)^{3\ln n/\ln\ln n}\\ &\lt \left(\frac{\ln\ln n}{\ln n}\right)^{3\ln n/\ln\ln n}\\ &= e^{3(\ln\ln\ln n-\ln\ln n)\ln n/\ln\ln n}\\ &\le e^{-3\ln n+3(\ln\ln n)(\ln n)/\ln\ln n}\\ &\le e^{-2\ln n}\\ &= \frac{1}{n^2}. \end{align} }[/math]
Therefore,
- [math]\displaystyle{ \begin{align} \Pr\left[\max_{1\le i\le n}X_i\ge \frac{3\ln n}{\ln\ln n}\right] &\le n\left(\frac{e}{M}\right)^M &\lt \frac{1}{n}. \end{align} }[/math]
- [math]\displaystyle{ \square }[/math]
When [math]\displaystyle{ m\gt n }[/math], Figure 1 illustrates the results of several random experiments, which show that the distribution of the loads of bins becomes more even as the number of balls grows larger than the number of bins.
Formally, it can be proved that for [math]\displaystyle{ m=\Omega(n\log n) }[/math], with high probability, the maximum load is within [math]\displaystyle{ O\left(\frac{m}{n}\right) }[/math], which is asymptotically equal to the average load.
Applications of balls-into-bins
Birthday attack
Suppose that [math]\displaystyle{ h:U\rightarrow[n] }[/math] is a cryptographic hash function that maps a large domain of items to a small range, i.e. we have that [math]\displaystyle{ |U|\gg n }[/math]. As a cryptographic hash function, [math]\displaystyle{ h }[/math] is deterministic and efficiently computable. The security of the crypto systems built from the hash function are usually based on the following properties of function:
- One-way-ness: Given a hash value [math]\displaystyle{ i\in[n] }[/math], it is hard to generate an [math]\displaystyle{ x\in U }[/math] that [math]\displaystyle{ h(x)=i }[/math].
- Weak collision resistance: Given an item [math]\displaystyle{ x\in U }[/math], it is hard to find an [math]\displaystyle{ x'\in U }[/math] that [math]\displaystyle{ x\neq x' }[/math] and [math]\displaystyle{ h(x)=h(x') }[/math]. Such [math]\displaystyle{ (x,x') }[/math] is called a collision pair.
- Strong collision resistance: It is hard to generate a collision pair.
It can be seen that the third property is the strongest one. Some digital signature schemes are based on this assumption.
The "birthday attack" is inspired by the birthday paradox. Uniformly and independently pick a number of random items from [math]\displaystyle{ U }[/math], with some fair probability, there is a collision pair among these randomly chosen items.
Suppose that we choose [math]\displaystyle{ m }[/math] items from [math]\displaystyle{ U }[/math]. We assume that [math]\displaystyle{ m=O(\sqrt{n}) }[/math]. Since [math]\displaystyle{ |U|\gg n }[/math], the probability that we pick the same item twice is [math]\displaystyle{ o(1) }[/math] (this can be seen as a birthday problem with very small number of students). The following arguments are conditioned on that all chosen items are different.
Therefore, we can view the hash values [math]\displaystyle{ [n] }[/math] as [math]\displaystyle{ n }[/math] bins, and hashing a random [math]\displaystyle{ x }[/math] to [math]\displaystyle{ h(x) }[/math] as throwing a ball into a bin. Conditioning on that all chosen items are different, a collision occurs if and only if a bin has more than one balls.
For each [math]\displaystyle{ i\in[n] }[/math], let [math]\displaystyle{ p_i=\frac{|h^{-1}(i)|}{|U|} }[/math] be the fraction of the domain mapped to hash value [math]\displaystyle{ i }[/math]. Obviously [math]\displaystyle{ \sum_{i\in[n]}p_i=1 }[/math].
If all [math]\displaystyle{ p_i }[/math] are equal that [math]\displaystyle{ p_i=\frac{1}{n} }[/math], i.e. the hash function maps the items evenly over its range, then each ball is thrown to a uniform bin. It is exactly as the birthday problem. Due to our analysis of the birthday problem, for some [math]\displaystyle{ m=O(\sqrt{n}) }[/math], there is a collision pair with probability [math]\displaystyle{ 999/1000 }[/math].
This argument is conditioned on that all chosen items are different. As we saw the probability that we choose the same item twice is only [math]\displaystyle{ o(1) }[/math], by union bound the probability that this occurs or no two balls are thrown to the same bins is [math]\displaystyle{ 1/1000+o(1) }[/math]. So the probability that a collision pair is found by the birthday attack is [math]\displaystyle{ 999/1000-o(1) }[/math].
What if [math]\displaystyle{ h }[/math] does not distribute items evenly over the range, i.e. [math]\displaystyle{ p_i }[/math]'s are different. We can partition each [math]\displaystyle{ p_i }[/math] into as many as possible "virtual bins" of probability mass [math]\displaystyle{ 1/2n }[/math], and sum the remainders to a single "garbage bin". It is easy to see that there are at most [math]\displaystyle{ 2n }[/math] virtual bins and the probability mass of the garbage bin is no more than 1/2. Then the problem is turned to throwing each of the [math]\displaystyle{ m }[/math] balls first to the garbage bin with probability at most 1/2, and if survived, to a uniformly random virtual bin.
Stable marriage
Suppose that there are [math]\displaystyle{ n }[/math] men and [math]\displaystyle{ n }[/math] women. Every man has a preference list of women, which can be represented as a permutation of [math]\displaystyle{ [n] }[/math]. Similarly, every women has a preference list of men, which is also a permutation of [math]\displaystyle{ [n] }[/math]. A marriage is a 1-1 correspondence between men and women. The stable marriage problem or stable matching problem (SMP) is to find a marriage which is stable in the following sense:
- There is no such a man and a woman who are not married to each other but prefer each other to their current partners.
The famous proposal algorithm (求婚算法) solves this problem by finding a stable marriage. The algorithm is described as follows:
- Each round (called a proposal)
- An unmarried man proposes to the most desirable woman according to his preference list who has not already rejected him.
- Upon receiving his proposal, the woman accepts the proposal if:
- she's not married; or
- her current partner is less desirable than the proposing man according to her preference list. (Her current partner then becomes available again.)
The algorithm terminates when the last available woman receives a proposal. The algorithm returns a marriage, because it is easy to see that:
- once a woman is proposed to, she gets married and stays as married (and will only switch to more desirable men.)
It can be seen that this algorithm always finds a stable marriage:
- If to the contrary, there is a man [math]\displaystyle{ A }[/math] and a woman [math]\displaystyle{ b }[/math] prefer each other than their current partners [math]\displaystyle{ a }[/math] ([math]\displaystyle{ A }[/math]'s wife) and [math]\displaystyle{ B }[/math] ([math]\displaystyle{ b }[/math]'s husband), then [math]\displaystyle{ A }[/math] must have proposed to [math]\displaystyle{ b }[/math] before he proposed to [math]\displaystyle{ a }[/math], by which time [math]\displaystyle{ b }[/math] must either be available or be with a worse man (because her current partner [math]\displaystyle{ B }[/math] is worse than [math]\displaystyle{ A }[/math]), which means [math]\displaystyle{ b }[/math] must have accepted [math]\displaystyle{ A }[/math]'s proposal.
Our interest is the average-case performance of this algorithm, which is measured by the expected number of proposals, assuming that each man/woman has a uniformly random permutation as his/her preference list.
Apply the principle of deferred decisions, each man can be seen as that at each time, sampling a uniformly random woman from the ones who have not already rejected him, and proposing to her. This can only be more efficient than sampling a uniformly and independently random woman to propose. All [math]\displaystyle{ n }[/math] men are proposing to uniformly and independently random woman, thus it can be seen as proposals (regardless which men they are from) are sent to women uniformly and independently at random. The algorithm ends when all [math]\displaystyle{ n }[/math] women have received a proposal. Due to our analysis of the coupon collector problem, the expected number of proposals is [math]\displaystyle{ O(n\ln n) }[/math].
Chain hashing and load balancing
Consider the following two scenarios:
- A hash table which resolves collisions by chaining, such that all keys mapped to the same slots are arranged by a linked list pointed from the slot.
- Distributed a number of jobs evenly among a set of machines by a random hash function.
With UHA, both scenarios can be viewed as a balls-into-bins game, and the loads of bins give the lengths of chains or the loads of machines. The maximum load of bins is critical, because it gives the worst-case searching time for the hash table and the finishing time for the machines.
By our assignment of the occupancy problem, when [math]\displaystyle{ m=\Theta(n) }[/math], the maximum load is [math]\displaystyle{ O(\ln n/\ln\ln n) }[/math] with high probability.