高级算法 (Fall 2024)/Hashing and Sketching

Balls into Bins

The following is the so-called balls into bins model. Consider throwing $m$ balls into $n$ bins uniformly and independently at random. This is equivalent to a random mapping $f:[m]\to [n]$. Needless to say, random mapping is an important random model and may have many applications in Computer Science, e.g. hashing.

We are concerned with the following three questions regarding the balls into bins model:

• birthday problem: the probability that every bin contains at most one ball (the mapping is 1-1);
• coupon collector problem: the probability that every bin contains at least one ball (the mapping is on-to);
• occupancy problem: the maximum load of bins.

Birthday Problem

We now consider the birthday problem. There are $m$ students in the class. Assume that for each student, his/her birthday is uniformly and independently distributed over the 365 days in a years. We wonder what the probability that no two students share a birthday.

Due to the pigeonhole principle, it is obvious that for $m>365$, there must be two students with the same birthday. Surprisingly, for any $m>57$ this event occurs with more than 99% probability. This is called the birthday paradox. Despite the name, the birthday paradox is not a real paradox.

We can model this problem as a balls-into-bins problem. $m$ different balls (students) are uniformly and independently thrown into 365 bins (days). More generally, let $n$ be the number of bins. We ask for the probability of the following event $\mathcal{E}$

• $\mathcal{E}$: there is no bin with more than one balls (i.e. no two students share birthday).

We first analyze this by counting. There are totally $n^m$ ways of assigning $m$ balls to $n$ bins. The number of assignments that no two balls share a bin is $(\genfrac{}{}{0ex}{}{n}{m})m!$.

Thus the probability is given by:

$\begin{array}{r}Pr[\mathcal{E}]=\frac{(\genfrac{}{}{0ex}{}{n}{m})m!}{n^m}.\end{array}$

Recall that $(\genfrac{}{}{0ex}{}{n}{m})=\frac{n!}{(n-m)!m!}$. Then

$\begin{array}{r}Pr[\mathcal{E}]=\frac{(\genfrac{}{}{0ex}{}{n}{m})m!}{n^m}=\frac{n!}{n^m(n-m)!}=\frac{n}{n}\cdot \frac{n-1}{n}\cdot \frac{n-2}{n}\cdots \frac{n-(m-1)}{n}=\prod _{k=1}^{m-1}(1-\frac{k}{n}).\end{array}$

There is also a more "probabilistic" argument for the above equation. Consider again that $m$ students are mapped to $n$ possible birthdays uniformly at random.

The first student has a birthday for sure. The probability that the second student has a different birthday from the first student is $(1-\frac{1}{n})$. Given that the first two students have different birthdays, the probability that the third student has a different birthday from the first two students is $(1-\frac{2}{n})$. Continuing this on, assuming that the first $k-1$ students all have different birthdays, the probability that the $k$th student has a different birthday than the first $k-1$, is given by $(1-\frac{k-1}{n})$. By the chain rule, the probability that all $m$ students have different birthdays is:

$\begin{array}{rl}Pr[\mathcal{E}]=(1-\frac{1}{n})\cdot (1-\frac{2}{n})\cdots (1-\frac{m-1}{n})& =\prod _{k=1}^{m-1}(1-\frac{k}{n}),\end{array}$

which is the same as what we got by the counting argument.

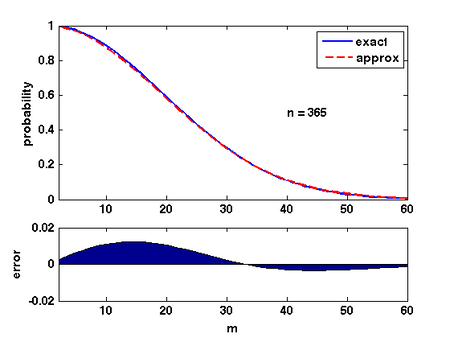
There are several ways of analyzing this formular. Here is a convenient one: Due to Taylor's expansion, $e^{-k/n}\approx 1-k/n$. Then

$\begin{array}{rl}\prod _{k=1}^{m-1}(1-\frac{k}{n})& \approx \prod _{k=1}^{m-1}{e}^{-\frac{k}{n}}\\ & =\exp (-\sum _{k=1}^{m-1}\frac{k}{n})\\ & =e^{-m(m-1)/2n}\\ & \approx e^{-m^2/2n}.\end{array}$

The quality of this approximation is shown in the Figure.

Therefore, for $m=\sqrt{2n\ln \frac{1}{ϵ}}$, the probability that $Pr[\mathcal{E}]\approx ϵ$.

Universal Hashing

Hashing is one of the oldest tools in Computer Science. Knuth's memorandum in 1963 on analysis of hash tables is now considered to be the birth of the area of analysis of algorithms.

• Knuth. Notes on "open" addressing, July 22 1963. Unpublished memorandum.

The idea of hashing is simple: an unknown set $S$ of $n$ data items (or keys) are drawn from a large universe $U=[N]$ where $N\gg n$; in order to store $S$ in a table of $M$ entries (slots), we assume a consistent mapping (called a hash function) from the universe $U$ to a small range $[M]$.

This idea seems clever: we use a consistent mapping to deal with an arbitrary unknown data set. However, there is a fundamental flaw for hashing.

• For sufficiently large universe ($N>M(n-1)$), for any function, there exists a bad data set $S$, such that all items in $S$ are mapped to the same entry in the table.

A simple use of pigeonhole principle can prove the above statement.

To overcome this situation, randomization is introduced into hashing. We assume that the hash function is a random mapping from $[N]$ to $[M]$. In order to ease the analysis, the following ideal assumption is used:

Simple Uniform Hash Assumption (SUHA or UHA, a.k.a. the random oracle model):

A uniform random function $h:[N]\to [M]$ is available and the computation of $h$ is efficient.

Families of universal hash functions

The assumption of completely random function simplifies the analysis. However, in practice, truly uniform random hash function is extremely expensive to compute and store. Thus, this simple assumption can hardly represent the reality.

There are two approaches for implementing practical hash functions. One is to use ad hoc implementations and wish they may work. The other approach is to construct class of hash functions which are efficient to compute and store but with weaker randomness guarantees, and then analyze the applications of hash functions based on this weaker assumption of randomness.

This route was took by Carter and Wegman in 1977 while they introduced universal families of hash functions.

Definition (universal hash families)

Let $[N]$ be a universe with $N\ge M$. A family of hash functions $\mathcal{H}$ from $[N]$ to $[M]$ is said to be $k$-universal if, for any distinct items $x_1,x_2,\dots ,x_k\in [N]$ and for a hash function $h$ chosen uniformly at random from $\mathcal{H}$, we have $Pr[h(x_1)=h(x_2)=\cdots =h(x_k)]\le \frac{1}{M^{k-1}}.$ A family of hash functions $\mathcal{H}$ from $[N]$ to $[M]$ is said to be strongly $k$-universal if, for any distinct items $x_1,x_2,\dots ,x_k\in [N]$, any values $y_1,y_2,\dots ,y_k\in [M]$, and for a hash function $h$ chosen uniformly at random from $\mathcal{H}$, we have $Pr[h(x_1)=y_1\wedge h(x_2)=y_2\wedge \cdots \wedge h(x_k)=y_k]=\frac{1}{M^k}.$

In particular, for a 2-universal family $\mathcal{H}$, for any distinct elements $x_1,x_2\in [N]$, a uniform random $h\in \mathcal{H}$ has

$Pr[h(x_1)=h(x_2)]\le \frac{1}{M}.$

For a strongly 2-universal family $\mathcal{H}$, for any distinct elements $x_1,x_2\in [N]$ and any values $y_1,y_2\in [M]$, a uniform random $h\in \mathcal{H}$ has

$Pr[h(x_1)=y_1\wedge h(x_2)=y_2]=\frac{1}{M^2}.$

This behavior is exactly the same as uniform random hash functions on any distinct pair of inputs. For this reason, a strongly 2-universal hash family are also called pairwise independent hash functions.

2-universal hash families

The construction of pairwise independent random variables via modulo a prime introduced in Section 1 already provides a way of constructing a strongly 2-universal hash family.

Let $p$ be a prime. The function $h_{a,b}:[p]\to [p]$ is defined by

$h_{a,b}(x)=(ax+b)modp,$

and the family is

$\mathcal{H}=\{h_{a,b}\mid a,b\in [p]\}.$

Lemma

$\mathcal{H}$ is strongly 2-universal.

Proof. In Section 1, we have proved the pairwise independence of the sequence of $(ai+b)modp$, for $i=0,1,\dots ,p-1$, which directly implies that $\mathcal{H}$ is strongly 2-universal. $◻$

The original construction of Carter-Wegman

What if we want to have hash functions from $[N]$ to $[M]$ for non-prime $N$ and $M$? Carter and Wegman developed the following method.

Suppose that the universe is $[N]$, and the functions map $[N]$ to $[M]$, where $N\ge M$. For some prime $p\ge N$, let

$h_{a,b}(x)=((ax+b)modp)modM,$

and the family

$\mathcal{H}=\{h_{a,b}\mid 1\le a\le p-1,b\in [p]\}.$

Note that unlike the first construction, now $a\ne 0$.

Lemma (Carter-Wegman)

$\mathcal{H}$ is 2-universal.

Proof. Due to the definition of $\mathcal{H}$, there are $p(p-1)$ many different hash functions in $\mathcal{H}$, because each hash function in $\mathcal{H}$ corresponds to a pair of $1\le a\le p-1$ and $b\in [p]$. We only need to count for any particular pair of $x_1,x_2\in [N]$ that $x_1\ne x_2$, the number of hash functions that $h(x_1)=h(x_2)$. We first note that for any $x_1\ne x_2$, $a{x}_1+b\not\equiv a{x}_2+b(\mathrm{mod}p)$. This is because $a{x}_1+b\equiv a{x}_2+b(\mathrm{mod}p)$ would imply that $a(x_1-x_2)\equiv 0(\mathrm{mod}p)$, which can never happen since $1\le a\le p-1$ and $x_1\ne x_2$ (note that $x_1,x_2\in [N]$ for an $N\le p$). Therefore, we can assume that $(a{x}_1+b)modp=u$ and $(a{x}_2+b)modp=v$ for $u\ne v$. By linear algebra (over finite field), for any $x_1,x_2\in [N]$ that $x_1\ne x_2$, for any $u,v\in [p]$ that $u\ne v$, there is exact one solution to $(a,b)$ satisfying: $\{\begin{array}{l}a{x}_1+b\equiv u(\mathrm{mod}p)\\ a{x}_2+b\equiv v(\mathrm{mod}p).\end{array}$ After modulo $M$, every $u\in [p]$ has at most $\lceil p/M\rceil -1$ many $v\in [p]$ that $v\ne u$ but $v\equiv u(\mathrm{mod}M)$. Therefore, for every pair of $x_1,x_2\in [N]$ that $x_1\ne x_2$, there exist at most $p(\lceil p/M\rceil -1)\le p(p-1)/M$ pairs of $1\le a\le p-1$ and $b\in [p]$ such that $((a{x}_1+b)modp)modM=((a{x}_2+b)modp)modM$, which means there are at most $p(p-1)/M$ many hash functions $h\in \mathcal{H}$ having $h(x_1)=h(x_2)$ for $x_1\ne x_2$. For $h$ uniformly chosen from $\mathcal{H}$, for any $x_1\ne x_2$, $Pr[h(x_1)=h(x_2)]\le \frac{p(p-1)/M}{p(p-1)}=\frac{1}{M}.$ We prove that $\mathcal{H}$ is 2-universal. $◻$

A construction used in practice

The main issue of Carter-Wegman construction is the efficiency. The mod operation is very slow, and has been so for more than 30 years.

The following construction is due to Dietzfelbinger et al. It was published in 1997 and has been practically used in various applications of universal hashing.

The family of hash functions is from $[2^u]$ to $[2^v]$. With a binary representation, the functions map binary strings of length $u$ to binary strings of length $v$. Let

$h_a(x)=\lfloor \frac{a\cdot xmod{2}^u}{2^{u-v}}\rfloor ,$

and the family

$\mathcal{H}=\{h_a\mid a\in [2^v]\text{ and }a\text{ is odd}\}.$

This family of hash functions does not exactly meet the requirement of 2-universal family. However, Dietzfelbinger et al proved that $\mathcal{H}$ is close to a 2-universal family. Specifically, for any distinct input values $x_1,x_2\in [2^u]$, for a uniformly random $h\in \mathcal{H}$,

$Pr[h(x_1)=h(x_2)]\le \frac{1}{2^{v-1}}.$

So $\mathcal{H}$ is within an approximation ratio of 2 to being 2-universal. The proof uses the fact that odd numbers are relative prime to a power of 2.

The function is extremely simple to compute in c language. We exploit that C-multiplication (*) of unsigned u-bit numbers is done $mod{2}^u$, and have a one-line C-code for computing the hash function:

h_a(x) = (a*x)>>(u-v)

The bit-wise shifting is a lot faster than modular. It explains the popularity of this scheme in practice than the original Carter-Wegman construction.

Collision number

Consider a 2-universal family $\mathcal{H}$ of hash functions from $[N]$ to $[M]$. Let $h$ be a hash function chosen uniformly from $\mathcal{H}$. For a fixed set $S$ of $n$ distinct elements from $[N]$, say $S=\{x_1,x_2,\dots ,x_n\}$, the elements are mapped to the hash values $h(x_1),h(x_2),\dots ,h(x_n)$. This can be seen as throwing $n$ balls to $M$ bins, with pairwise independent choices of bins.

As in the balls-into-bins with full independence, we are curious about the questions such as the birthday problem or the maximum load. These questions are interesting not only because they are natural to ask in a balls-into-bins setting, but in the context of hashing, they are closely related to the performance of hash functions.

The old techniques for analyzing balls-into-bins rely too much on the independence of the choice of the bin for each ball, therefore can hardly be extended to the setting of 2-universal hash families. However, it turns out several balls-into-bins questions can somehow be answered by analyzing a very natural quantity: the number of collision pairs.

A collision pair for hashing is a pair of elements $x_1,x_2\in S$ which are mapped to the same hash value, i.e. $h(x_1)=h(x_2)$. Formally, for a fixed set of elements $S=\{x_1,x_2,\dots ,x_n\}$, for any $1\le i,j\le n$, let the random variable

$X_{ij}=\{\begin{array}{ll}1& \text{if }h(x_i)=h(x_j),\\ 0& \text{otherwise.}\end{array}$

The total number of collision pairs among the $n$ items $x_1,x_2,\dots ,x_n$ is

$X=\sum _{i<j}{X}_{ij}.$

Since $\mathcal{H}$ is 2-universal, for any $i\ne j$,

$Pr[X_{ij}=1]=Pr[h(x_i)=h(x_j)]\le \frac{1}{M}.$

The expected number of collision pairs is

$\mathbf{E}[X]=\mathbf{E}\left[\sum _{i<j}{X}_{ij}\right]=\sum _{i<j}\mathbf{E}[X_{ij}]=\sum _{i<j}Pr[X_{ij}=1]\le (\genfrac{}{}{0ex}{}{n}{2})\frac{1}{M}<\frac{n^2}{2M}.$

In particular, for $n=M$, i.e. $n$ items are mapped to $n$ hash values by a pairwise independent hash function, the expected collision number is $\mathbf{E}[X]<\frac{n^2}{2M}=\frac{n}{2}$.

The above analysis gives us an estimation on the expected number of collision pairs, such that $\mathbf{E}[X]<\frac{n^2}{2M}$. Apply the Markov's inequality, for $0<ϵ<1$, we have

$Pr[X\ge \frac{n^2}{2ϵM}]\le Pr[X\ge \frac{1}{ϵ}\mathbf{E}[X]]\le ϵ.$

When $n\le \sqrt{2ϵM}$, the number of collision pairs is $X\ge 1$ with probability at most $ϵ$, therefore with probability at least $1-ϵ$, there is no collision at all. Therefore, we have the following theorem.

Theorem

If $h$ is chosen uniformly from a 2-universal family of hash functions mapping the universe $[N]$ to $[M]$ where $N\ge M$, then for any set $S\subset [N]$ of $n$ items, where $n\le \sqrt{2ϵM}$, the probability that there exits a collision pair is $Pr[\text{collision occurs}]\le ϵ.$

Recall that for mutually independent choices of bins, for some $n=\sqrt{2M\ln (1/ϵ)}$, the probability that a collision occurs is about $ϵ$. For constant $ϵ$, this gives an essentially same bound as the pairwise independent setting. Therefore, the behavior of pairwise independent hash function is essentially the same as the uniform random hash function for the birthday problem. This is easy to understand, because birthday problem is about the behavior of collisions, and the definition of 2-universal hash function can be interpreted as "functions that the probability of collision is as low as a uniform random function".

Set Membership

A basic question in Computer Science is:

"$\text{Is }x\in S?$"

for a set $S$ and an element $x$. This is the set membership problem.

Formally, given an arbitrary set $S$ of $n$ elements from a universe $U$, we want to use a succinct data structure to represent this set $S$, so that upon each query of any element $x$ from the universe $[N]$, the question of whether $x\in S$ is efficiently answered. The complexity of such data structure is measured in two-fold:

• space cost: size of the data structure to represent a set $S$ of size $n$;
• time cost: time complexity of answering each query by accessing to the data structure.

Suppose that the universe $U$ is of size $N$. Clearly, the membership problem can be solved by a dictionary data structure, e.g.:

• sorted table / balanced search tree: with space cost $O(n\log N)$ bits and time cost $O(\log n)$.

Note that $\log (\genfrac{}{}{0ex}{}{N}{n})=\mathrm{\Theta }(n\log \frac{N}{n})$ is the entropy of sets $S$ of $n$ elements from a universe $U$ of size $N$. Therefore it is necessary to use so many bits to represent a set without losing any information. With hashing, we can solve this fundamental problem with asymptotic optimal space cost and time cost at the same time.

Perfect hashing using quadratic space

The idea of perfect hashing is that we use a hash function $h$ to map the $n$ items to distinct entries of the table; store every item $x\in S$ in the entry $h(x)$; and also store the hash function $h$ in a fixed location in the table (usually the beginning of the table). The algorithm for searching for an item is as follows:

search for $x$ in table $T$:

1. retrieve $h$ from a fixed location in the table;
2. if $x=T[h(x)]$ return $h(x)$; else return NOT_FOUND;

This scheme works as long as that the hash function satisfies the following two conditions:

• The description of $h$ is sufficiently short, so that $h$ can be stored in one entry (or in constant many entries) of the table.
• $h$ has no collisions on $S$, i.e. there is no pair of items $x_1,x_2\in S$ that are mapped to the same value by $h$.

The first condition is easy to guarantee for 2-universal hash families. As shown by Carter-Wegman construction, a 2-universal hash function can be uniquely represented by two integers $a$ and $b$, which can be stored in two entries (or just one, if the word length is sufficiently large) of the table.

Our discussion is now focused on the second condition. We find that it relies on the perfectness of the hash function for a data set $S$.

A hash function $h$ is perfect for a set $S$ of items if $h$ maps all items in $S$ to different values, i.e. there is no collision.

We have shown by the birthday problem for 2-universal hashing that when $n$ items are mapped to $n^2$ values, for an $h$ chosen uniformly from a 2-universal family of hash functions, the probability that a collision occurs is at most 1/2. Thus

$Pr[h\text{ is perfect for }S]\ge \frac{1}{2}$

for a table of $n^2$ entries.

The construction of perfect hashing is straightforward then:

For a set $S$ of $n$ elements:

1. uniformly choose an $h$ from a 2-universal family $\mathcal{H}$; (for Carter-Wegman's construction, it means uniformly choose two integer $1\le a\le p-1$ and $b\in [p]$ for a sufficiently large prime $p$.)
2. check whether $h$ is perfect for $S$;
3. if $h$ is NOT perfect for $S$, start over again; otherwise, construct the table;

This is a Las Vegas randomized algorithm, which construct a perfect hashing for a fixed set $S$ with expectedly at most two trials (due to geometric distribution). The resulting data structure is a $O(n^2)$-size static dictionary of $n$ elements which answers every search in deterministic $O(1)$ time.

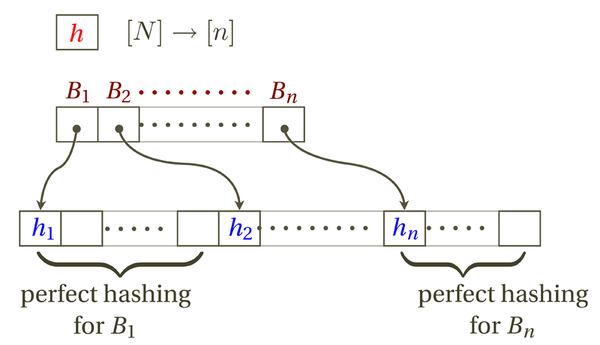
FKS perfect hashing

In the last section we see how to use $O(n^2)$ space and constant time for answering search in a set. Now we see how to do it with linear space and constant time. This solves the problem of searching asymptotically optimal for both time and space.

This was once seemingly impossible, until Yao's seminal paper:

• Yao. Should tables be sorted? Journal of the ACM (JACM), 1981.

Yao's paper shows a possibility of achieving linear space and constant time at the same time by exploiting the power of hashing, but assumes an unrealistically large universe.

Inspired by Yao's work, Fredman, Komlós, and Szemerédi discover the first linear-space and constant-time static dictionary in a realistic setting:

• Fredman, Komlós, and Szemerédi. Storing a sparse table with O(1) worst case access time. Journal of the ACM (JACM), 1984.

The idea of FKS hashing is to arrange hash table in two levels:

• In the first level, $n$ items are hashed to $n$ buckets by a 2-universal hash function $h$.

Let $B_i$ be the set of items hashed to the $i$th bucket.

• In the second level, construct a $|B_i{|}^2$-size perfect hashing for each bucket $B_i$.

The data structure can be stored in a table. The first few entries are reserved to store the primary hash function $h$. To help the searching algorithm locate a bucket, we use the next $n$ entries of the table as the "pointers" to the bucket: each entry stores the address of the first entry of the space to store a bucket. In the rest of table, the $n$ buckets are stored in order, each using a $|B_i{|}^2$ space as required by perfect hashing.

It is easy to see that the search time is constant. To search for an item $x$, the algorithm does the followings:

• Retrieve $h$.
• Retrieve the address for bucket $h(x)$.
• Search by perfect hashing within bucket $h(x)$.

Each line takes constant time. So the worst-case search time is constant.

We then need to guarantee that the space is linear to $n$. At the first glance, this seems impossible because each instance of perfect hashing for a bucket costs a square-size of space. We will prove that although the individual buckets use square-sized spaces, the sum of the them is still linear.

For a fixed set $S$ of $n$ items, for a hash function $h$ chosen uniformly from a 2-universe family which maps the items to $[n]$, called $n$ buckets, let $Y_i=|B_i|$ be the number of items in $S$ mapped to the $i$th bucket. We are going to bound the following quantity:

$Y=\sum _{i=1}^n{Y}_i^2.$

Since each bucket $B_i$ use a space of $Y_i^2$ for perfect hashing. $Y$ gives the size of the space for storing the buckets.

We will show that $Y$ is related to the total number of collision pairs. (Indeed, the number of collision pairs can be computed by a degree-2 polynomial, just like $Y$.)

Note that a bucket of $Y_i$ items contributes $(\genfrac{}{}{0ex}{}{Y_i}{2})$ collision pairs. Let $X$ be the total number of collision pairs. $X$ can be computed by summing over the collision pairs in every bucket:

$X=\sum _{i=1}^n(\genfrac{}{}{0ex}{}{Y_i}{2})=\sum _{i=1}^n\frac{Y_i(Y_i-1)}{2}=\frac{1}{2}(\sum _{i=1}^n{Y}_i^2-\sum _{i=1}^n{Y}_i)=\frac{1}{2}(\sum _{i=1}^n{Y}_i^2-n).$

Therefore, the sum of squares of the sizes of buckets is related to collision number by:

$\sum _{i=1}^n{Y}_i^2=2X+n.$

By our analysis of the collision number, we know that for $n$ items mapped to $n$ buckets, the expected number of collision pairs is: $\mathbf{E}[X]\le \frac{n}{2}$. Thus,

$\mathbf{E}\left[\sum _{i=1}^n{Y}_i^2\right]=\mathbf{E}[2X+n]\le 2n.$

Due to Markov's inequality, $\sum _{i=1}^n{Y}_i^2=O(n)$ with a constant probability. For any set $S$, we can find a suitable $h$ after expected constant number of trials, and FKS can be constructed with guaranteed (instead of expected) linear-size which answers each search in constant time.

Bloom filter

Now we consider the lossy representation of the original data set $S$, to further save the space usage. Such lossy data structure is sometimes called a sketch.

The Bloom filter is such a lossy data structure. It is a space-efficient hash table that solves the approximate membership problem with one-sided error (false positive).

Given a set $S$ of $n$ elements from a universe $U$, a Bloom filter consists of an array $A$ of $cn$ bits, and $k$ hash functions $h_1,h_2,\dots ,h_k$ map $U$ to $[cn]$, where both $c$ and $k$ are parameters that we can try to optimize later.

As before, we assume the Uniform Hash Assumption (UHA): $h_1,h_2,\dots ,h_k$ are mutually independent hash function where each $h_i$ is a uniform random hash function $h_i:U\to [cn]$.

The Bloom filter works as follows:

Bloom filter (Bloom 1970)

Suppose $h_1,h_2,\dots ,h_k:U\to [cn]$ are uniform and independent random hash functions. Data structure construction: Given a set $S\subset U$ of size $n=|S|$, the data structure is a Boolean array $A$ of $cn$ bits constructed as initialize all $cn$ bits of the Boolean array $A$ to 0; for each $x\in S$, let $A[h_i(x)]=1$ for all $1\le i\le k$. Query resolution: Upon each query of an arbitrary $x\in U$, answer "yes" if $A[h_i(x)]=1$ for all $1\le i\le k$ and "no" if otherwise.

The Boolean array is our data structure, whose size is $cn$ bits. With Uniform Hash Assumption (UHA), the time cost of the data structure for answering each query is $O(k)$.

When the answer returned by the algorithm is "no", it holds that $A[h_i(x)]=0$ for some $1\le i\le k$, in which case the query $x$ must not belong to the set $S$. Thus, the Bloom filter has no false negatives.

On the other hand, when the answer returned by the algorithm is "yes", $A[h_i(x)]=1$ for all $1\le i\le k$. It is still possible for some $x\notin S$ that all bits $A[h_i(x)]$ are set by elements in $S$. We want to bound such false positive, that is, the following probability for an $x\notin S$:

$Pr[\mathrm{\forall }1\le i\le k,A[h_i(x)]=1]$,

which by independence between different hash functions and by symmetry is equal to:

$Pr[A[h_1(x)]=1{]}^k=(1-Pr[A[h_1(x)]=0]{)}^k$.

For an element $x\notin S$, its hash value $h_1(x)$ is independent of all hash values $h_i(y)$ for all $1\le i\le k$ and all $y\in S$. This is due to the Uniform Hash Assumption. The hash value $h_1(x)$ of $x\notin S$ is then independent of the content of the array $A$. Therefore, the probability of this position $A[h_1(x)]$ missed by all $kn$ updates to the Boolean array $A$ caused by all $n$ elements in $S$ is:

$Pr[A[h_1(x)]=0]={(1-\frac{1}{cn})}^{kn}\approx e^{-k/c}.$

Putting everything together, for any $x\notin S$, the false positive is bounded as:

$\begin{array}{rl}Pr[\text{wrongly answer ''yes''}]& =Pr[\mathrm{\forall }1\le i\le k,A[h_i(x)]=1]\\ & =Pr[A[h_1(x)]=1{]}^k=(1-Pr[A[h_1(x)]=0]{)}^k\\ & ={(1-{(1-\frac{1}{cn})}^{kn})}^k\\ & \approx {(1-e^{-k/c})}^k\end{array}$

which is $(0.6185{)}^c$ when $k=c\ln 2$.

Bloom filter solves the membership query with a small constant error of false positives using a data structure of $O(n)$ bits which answers each query with $O(1)$ time cost.

Distinct Elements

Consider the following problem of counting distinct elements: Suppose that $U$ is a sufficiently large universe.

• Input: a sequence of (not necessarily distinct) elements $x_1,x_2,\dots ,x_n\in U$;
• Output: an estimation of the total number of distinct elements $z=|\{x_1,x_2,\dots ,x_n\}|$.

A straightforward way of solving this problem is to maintain a dictionary data structure, which costs at least linear ($O(n)$) space. For big data, where $n$ is very large, this is still too expensive. However, due to an information-theoretical argument, linear space is necessary if you want to compute the exact value of $z$.

Our goal is to relax the problem a little bit to significantly reduce the space cost by tolerating approximate answers. The form of approximation we consider is $(ϵ,\delta )$-estimator.

$(ϵ,\delta )$-estimator

A random variable $\hat{Z}$ is an $(ϵ,\delta )$-estimator of a quantity $z$ if $Pr[(1-ϵ)z\le \hat{Z}\le (1+ϵ)z]\ge 1-\delta$. $\hat{Z}$ is said to be an unbiased estimator of $z$ if $\mathbb{E}[\hat{Z}]=z$.

Usually $ϵ$ is called approximation error and $\delta$ is called confidence error.

We now present an elegant algorithm. The algorithm can be implemented in data stream model: The input elements $x_1,x_2,\dots ,x_n$ is presented to the algorithm one at a time, where the size of data $n$ is unknown to the algorithm. The algorithm maintains a value $\hat{Z}$ which is an $(ϵ,\delta )$-estimator of the total number of distinct elements $z=|\{x_1,x_2,\dots ,x_n\}|$, using only a small amount of memory space to memorize (with loss) the data set $\{x_1,x_2,\dots ,x_n\}$.

A famous quotation of Flajolet describes the performance of this algorithm as:

"Using only memory equivalent to 5 lines of printed text, you can estimate with a typical accuracy of 5% and in a single pass the total vocabulary of Shakespeare."

The $min$-sketch

Suppose that we can access to an idealized random hash function $h:U\to [0,1]$ which is uniformly distributed over all mappings from the universe $U$ to unit interval $[0,1]$.

Recall that the input sequence $x_1,x_2,\dots ,x_n\in U$ consists of $z=|\{x_1,x_2,\dots ,x_n\}|$ distinct elements. These elements are mapped by the random function $h$ to $z$ hash values uniformly and independently distributed in $[0,1]$. We could maintain these hash values instead of the original elements, but this would still be too expensive because in the worst case we still have up to $n$ distinct values to maintain. However, due to the idealized random hash function, the unit interval $[0,1]$ will be partitioned into $z+1$ subintervals by these $z$ uniform and independent hash values. The typical length of the subinterval gives an estimation of the number $z$.

Proposition

$\mathbb{E}[\underset{1\le i\le n}{min}h(x_i)]=\frac{1}{z+1}$.

Proof. The input sequence $x_1,x_2,\dots ,x_n\in U$ consisting of $z$ distinct elements are mapped to $z$ random hash values uniformly and independently distributed in $[0,1]$. These $z$ hash values partition the unit interval $[0,1]$ into $z+1$ subintervals $[0,v_1],[v_1,v_2],[v_2,v_3]\dots ,[v_{z-1},v_z],[v_z,1]$, where $v_i$ denotes the $i$-th smallest value among all hash values $\{h(x_1),h(x_2),\dots ,h(x_n)\}$. Clearly we have $v_1=\underset{1\le i\le n}{min}h(x_i)$. Meanwhile, since all hash values are uniformly and independently distributed in $[0,1]$, the lengths of all subintervals $v_1,v_2-v_1,v_3-v_2,\dots ,v_z-v_{z-1},1-v_z$ are identically distributed. By symmetry, they have the same expectation, therefore $(z+1)\mathbb{E}[v_1]=\mathbb{E}[v_1]+\sum _{i=1}^{z-1}\mathbb{E}[v_{i+1}-v_i]+\mathbb{E}[1-v_z]=\mathbb{E}[v_1+(v_2-v_1)+(v_3-v_2)+\cdots +(v_z-v_{z-1})+1-v_z]=1,$ which implies that $\mathbb{E}[\underset{1\le i\le n}{min}h(x_i)]=\mathbb{E}[v_1]=\frac{1}{z+1}$. $◻$

The quantity $\underset{1\le i\le n}{min}h(x_i)$ can be computed with small space cost (for storing the current smallest hash value) by scan the input sequence in a single pass. Because as we proved its expectation is $\frac{1}{z+1}$, the smallest hash value $Y=\underset{1\le i\le n}{min}h(x_i)$ gives an unbiased estimator for $\frac{1}{z+1}$. However, $\frac{1}{Y}-1$ is not necessarily a good estimator for $z$. Actually, it is a rather poor estimator. Consider for example when $z=1$, all input elements are the same. In this case, there is only one hash value and $Y=\underset{1\le i\le n}{min}h(x_i)$ is distributed uniformly over $[0,1]$, thus $\frac{1}{Y}-1$ fails to be close enough to the correct answer 1 with high probability.

Apply the mean trick to the $min$-sketch

The reason that the above estimator of a single hash function performs poorly is that the unbiased estimator $\underset{1\le i\le n}{min}h(x_i)$ has large variance. So a natural way to reduce this variance is to have multiple independent hash functions and take the average. This generic approach for reducing the variance is called the mean trick.

Suppose that we can access to $k$ independent random hash functions $h_1,h_2,\dots ,h_k$, where each $h_j:U\to [0,1]$ is uniformly and independently distributed over all functions mapping $U$ to $[0,1]$. Here $k$ is a parameter to be fixed by the desired approximation error $ϵ$ and confidence error $\delta$. The $min$-sketch algorithm (using the mean trick) is given by the following pseudocode.

The $min$-sketch

Suppose that $h_1,h_2,\dots ,h_k:U\to [0,1]$ are $k$ uniform and independent random hash functions, where $k$ is a parameter to be fixed later. Scan the input sequence $x_1,x_2,\dots ,x_n\in U$ in a single pass to compute: $Y_j=\underset{1\le i\le n}{min}{h}_j(x_i)$ for every $j=1,2,\dots ,k$; average value $\overline{Y}=\frac{1}{k}\sum _{j=1}^k{Y}_j$; return $\hat{Z}=\frac{1}{\overline{Y}}-1$ as the estimator.

The algorithm is easy to implement in data stream model, with a space cost of storing $k$ hash values. The following theorem guarantees that the algorithm returns an $(ϵ,\delta )$-estimator of the total number of distinct elements for a suitable $k=O\left(\frac{1}{{ϵ}^2\delta }\right)$.

Theorem

For any $ϵ,\delta <1/2$, if $k\ge \lceil \frac{4}{{ϵ}^2\delta }\rceil$ then the output $\hat{Z}$ always gives an $(ϵ,\delta )$-estimator of the correct answer $z$.

In the following we prove this main theorem for $min$-sketch algorithm.

An obstacle to analyze the estimator $\hat{Z}=\frac{1}{\overline{Y}}-1$ is that it is a nonlinear function of $\overline{Y}$ who is easier to analyze. Nevertheless, we observe that $\hat{Z}$ is an $(ϵ,\delta )$-estimator of $z$ as long as $\overline{Y}$ is an $(ϵ/2,\delta )$-estimator of $\frac{1}{z+1}$. This can be deduced by just verifying the following:

$\frac{1-ϵ/2}{z+1}\le \overline{Y}\le \frac{1+ϵ/2}{z+1}⟹(1-ϵ)z\le \frac{1}{\overline{Y}}-1\le (1+ϵ)z$,

for $ϵ<\frac{1}{2}$. Therefore,

$Pr[(1-ϵ)z\le \hat{Z}\le (1+ϵ)z]\ge Pr[\frac{1-ϵ/2}{z+1}\le \overline{Y}\le \frac{1+ϵ/2}{z+1}]=Pr[|\overline{Y}-\frac{1}{z+1}|\le \frac{ϵ/2}{z+1}]$.

It is then sufficient to show that $Pr[|\overline{Y}-\frac{1}{z+1}|\le \frac{ϵ/2}{z+1}]\ge 1-\delta$ for proving the main theorem above. We will see that this is equivalent to show the concentration inequality

$Pr[|\overline{Y}-\mathbb{E}\left[\overline{Y}\right]|\le \frac{ϵ/2}{z+1}]\ge 1-\delta (\ast )$.

Lemma

The followings hold for each $Y_j$, $j=1,2\dots ,k$, and $\overline{Y}=\frac{1}{k}\sum _{j=1}^k{Y}_j$: $\mathbb{E}\left[\overline{Y}\right]=\mathbb{E}\left[Y_j\right]=\frac{1}{z+1}$; $\mathbf{V}\mathbf{a}\mathbf{r}\left[Y_j\right]\le \frac{1}{(z+1{)}^2}$, and consequently $\mathbf{V}\mathbf{a}\mathbf{r}\left[\overline{Y}\right]\le \frac{1}{k(z+1{)}^2}$.

Proof. As in the case of single hash function, by symmetry it holds that $\mathbb{E}[Y_j]=\frac{1}{z+1}$ for every $j=1,2,\dots ,k$. Therefore, $\mathbb{E}\left[\overline{Y}\right]=\frac{1}{k}\sum _{j=1}^k\mathbb{E}[Y_j]=\frac{1}{z+1}$. Recall that each $Y_j$ is the minimum of $z$ random hash values uniformly and independently distributed over $[0,1]$. By geometry probability, it holds that for any $y\in [0,1]$, $Pr[Y_j>y]=(1-y{)}^z$, which means $Pr[Y_j\le y]=1-(1-y{)}^z$. Taking the derivative with respect to $y$, we obtain the probability density function of random variable $Y_j$, which is $z(1-y{)}^{z-1}$. We then compute the second moment. $\mathbb{E}[Y_j^2]={\int }_0^1{y}^{2}z(1-y{)}^{z-1}\mathrm{d}y=\frac{2}{(z+1)(z+2)}$. The variance is bounded as $\mathbf{V}\mathbf{a}\mathbf{r}\left[Y_j\right]=\mathbb{E}\left[Y_j^2\right]-\mathbb{E}{\left[Y_j\right]}^2=\frac{2}{(z+1)(z+2)}-\frac{1}{(z+1{)}^2}\le \frac{1}{(z+1{)}^2}$. Due to the (pairwise) independence between $Y_j$'s, $\mathbf{V}\mathbf{a}\mathbf{r}\left[\overline{Y}\right]=\mathbf{V}\mathbf{a}\mathbf{r}\left[\frac{1}{k}\sum _{j=1}^k{Y}_j\right]=\frac{1}{k^2}\sum _{j=1}^k\mathbf{V}\mathbf{a}\mathbf{r}\left[Y_j\right]\le \frac{1}{k(z+1{)}^2}$. $◻$

We resume to prove the inequality $(\ast )$. By Chebyshev's inequality, it holds that

$Pr[|\overline{Y}-\mathbb{E}\left[\overline{Y}\right]|>\frac{ϵ/2}{z+1}]\le \frac{4}{{ϵ}^2}(z+1{)}^2\mathbf{V}\mathbf{a}\mathbf{r}\left[\overline{Y}\right]\le \frac{4}{{ϵ}^{2}k}$.

When $k\ge \lceil \frac{4}{{ϵ}^2\delta }\rceil$, this probability is at most $\delta$. The inequality $(\ast )$ is proved. As we discussed above, this proves the above main theorem $min$-sketch algorithm improved by the mean trick.

Frequency Estimation

Suppose that $U$ is the data universe. The frequency estimation problem is defined as follows.

• Data: a sequence of (not necessarily distinct) elements $x_1,x_2,\dots ,x_n\in U$;
• Query: an element $x\in U$;
• Output: an estimation ${\hat{f}}_x$ of the frequency $f_x\triangleq |\{i\mid x_i=x\}|$ of $x$ in input data.

We still want to give an algorithm in the data stream model: the algorithm scan the input sequence $x_1,x_2,\dots ,x_n$ to construct a succinct data structure, such that upon each query of $x\in U$, the algorithm returns an estimation of the frequency $f_x$.

Clearly this problem can always be solved by storing all appeared distinct elements along with their frequencies. However, the space cost of this straightforward solution is rather high. Instead, we want to use a lossy representation (a sketch) of input data which uses significantly less space but can still answer queries with tolarable accuracy.

Formally, upon each query of $x\in U$, the algorithm should return an answer ${\hat{f}}_x$ satisfying:

$Pr[|{\hat{f}}_x-f_x|\le ϵn]\ge 1-\delta$.

Note that this notion of approximation is with bounded additive error which is weaker than the notion of $(ϵ,\delta )$-estimator, whose error bound is multiplicative.

With such weak accuracy guarantee, its is possible to give a succinct data structure whose size is determined only by the error bounds $ϵ$ and $\delta$ but independent of $n$, because only the frequencies of those heavy hitters (elements $x$ with high frequencies $f_x>ϵn$) need to be memorized, and there are at most $1/ϵ$ many such heavy hitters.

Count-min sketch

The count-min sketch given by Cormode and Muthukrishnan is an elegant data structure for frequency estimation.

The data structure is a two-dimensional $k\times m$ integer array, where $k$ and $m$ are two parameters to be determined by the error bounds $ϵ$ and $\delta$. We still adopt the Uniform Hash Assumption to assume that we have access to $k$ mutually independent uniform random hash functions $h_1,h_2,\dots ,h_k:U\to [m]$.

Count-min sketch (Cormode and Muthukrishnan 2003)

Suppose $h_1,h_2,\dots ,h_k:U\to [m]$ are uniform and independent random hash functions. Data structure construction: Given a sequence $x_1,x_2,\dots ,x_n\in U$, the data structure is a two-dimensional $k\times m$ integer array $CMS[k][m]$ constructed as initialize all entries of $CMS[k][m]$ to 0; for $i=1,2,\dots ,n$, upon receiving $x_i$: for every $1\le j\le k$, evaluate $h_j(x_i)$ and $CMS[j][h_j(x_i)]++$. Query resolution: Upon each query of an arbitrary $x\in U$, return ${\hat{f}}_x=\underset{1\le j\le k}{min}CMS[j][h_j(x)]$.

It is easy to see that the space cost of count-min sketch is $O(km)$ memory words, or $O(km\log n)$ bits. Each query is answered within time cost $O(k)$, assuming that an evaluation of hash function can be done in unit or constant time. We then analyze the error bounds.

First, it is easy to observe that for any query $x\in U$ and every hash function $1\le j\le k$, it always holds for the corresponding entry in the count-min sketch

$CMS[j][h_j(x)]\ge f_x$,

because the appearances of element $x$ in the input sequence contribute at least $f_x$ to the value of $CMS[j][h_j(x)]$.

Therefore, for any query $x\in U$ it always holds for the answer ${\hat{f}}_x=\underset{1\le j\le k}{min}CMS[j][h_j(x)]\ge f_x$, which means

$Pr[|{\hat{f}}_x-f_x|\ge ϵn]=Pr[{\hat{f}}_x-f_x\ge ϵn]=\prod _{j=1}^{k}Pr[CMS[j][h_j(x)]-f_x\ge ϵn],(\mathrm{♢})$

where the second equation is due to the mutual independence of random hash functions $h_1,h_2,\dots ,h_k$.

It remains to upper bound the probability $Pr[CMS[j][h_j(x)]-f_x\ge ϵn]$, which can be done by calculating the expectation of $CMS[j][h_j(x)]$.

Proposition

For any $x\in U$ and every $1\le j\le k$, it holds that $\mathbb{E}[CMS[j][h_j(x)]]\le f_x+\frac{n}{m}$.

Proof. The value of $CMS[j][h_j(x)]$ is constituted by the frequency $f_x$ of $x$ and the frequencies $f_y$ of all other elements $y\ne x$ among $x_1,x_2,\dots ,x_n$, thus $\begin{array}{rl}CMS[j][h_j(x)]& =f_x+\sum _{\genfrac{}{}{0ex}{}{y\in \{x_1,\dots ,x_n\}\setminus \{x\}}{h_j(y)=h_j(x)}}{f}_y\\ & =f_x+\sum _{y\in \{x_1,\dots ,x_n\}\setminus \{x\}}{f}_y\cdot I[h_j(y)=h_j(x)]\end{array}$ where $I[h_j(y)=h_j(x)]$ denotes the Boolean random variable that indicates the occurrence of event $h_j(y)=h_j(x)$. By linearity of expectation, $\mathbb{E}[CMS[j][h_j(x)]]=f_x+\sum _{y\in \{x_1,x_2,\dots ,x_n\}\setminus \{x\}}{f}_y\cdot Pr[h_j(y)=h_j(x)]$. Due to Uniform Hash Assumption (UHA), $h_j:U\to [m]$ is a uniform random function. For any $y\ne x$, the probability of hash collision is $Pr[h_j(y)=h_j(x)]=\frac{1}{m}$. Therefore, $\begin{array}{rl}\mathbb{E}[CMS[j][h_j(x)]]& =f_x+\frac{1}{m}\sum _{y\in \{x_1,\dots ,x_n\}\setminus \{x\}}{f}_y\\ & \le f_x+\frac{1}{m}\sum _{y\in \{x_1,\dots ,x_n\}}{f}_y\\ & =f_x+\frac{n}{m},\end{array}$ where the last equation is due to the obvious identity $\sum _{y\in \{x_1,\dots ,x_n\}}{f}_y=n$. $◻$

The above proposition shows that for any $x\in U$ and every $1\le j\le k$

$\mathbb{E}[CMS[j][h_j(x)]-f_x]\le \frac{n}{m}$.

Recall that $CMS[j][h_j(x)]\ge f_x$ always holds, thus $CMS[j][h_j(x)]-f_x$ is a positive random variable. By Markov's inequality, we have

$Pr[CMS[j][h_j(x)]-f_x\ge ϵn]\le \frac{1}{ϵm}$.

Combining with above equation $(\mathrm{♢})$, we have

$Pr[|{\hat{f}}_x-f_x|\ge ϵn]=(Pr[CMS[j][h_j(x)]-f_x\ge ϵn]{)}^k\le \frac{1}{(ϵm{)}^k}$.

By setting $m=\lceil \frac{\mathrm{e}}{ϵ}\rceil$ and $k=\lceil \ln \frac{1}{\delta }\rceil$, the above error probability is bounded as $\frac{1}{(ϵm{)}^k}\le \delta$.

For any positive $ϵ$ and $\delta$, the count-min sketch gives a data structure of size $O(km)=O(\frac{1}{ϵ}\log \frac{1}{\delta })$ (in memory words) and answering each query $x\in U$ in time $O(k)=O\left(\frac{1}{ϵ}\right)$ with the following accuracy guarantee:

$Pr[|{\hat{f}}_x-f_x|\le ϵn]\ge 1-\delta$.