概率论与数理统计 (Spring 2023)/Karger's min-cut algorithm
Let [math]\displaystyle{ G(V, E) }[/math] be an undirected graph. A subset [math]\displaystyle{ C\subseteq E }[/math] of edges is a cut of graph [math]\displaystyle{ G }[/math] if [math]\displaystyle{ G }[/math] becomes disconnected after deleting all edges in [math]\displaystyle{ C }[/math].
Let [math]\displaystyle{ \{S,T\} }[/math] be a bipartition of [math]\displaystyle{ V }[/math] into nonempty subsets [math]\displaystyle{ S,T\subseteq V }[/math], where [math]\displaystyle{ S\cap T=\emptyset }[/math] and [math]\displaystyle{ S\cup T=V }[/math]. A cut [math]\displaystyle{ C }[/math] is specified by this bipartition as
- [math]\displaystyle{ C=E(S,T)\, }[/math],
where [math]\displaystyle{ E(S,T) }[/math] denotes the set of "crossing edges" with one endpoint in each of [math]\displaystyle{ S }[/math] and [math]\displaystyle{ T }[/math], formally defined as
- [math]\displaystyle{ E(S,T)=\{uv\in E\mid u\in S, v\in T\} }[/math].
The min-cut problem, also called the global minimum cut problem, is defined as follows.
Min-cut problem - Input: an undirected graph [math]\displaystyle{ G(V,E) }[/math];
- Output: a cut [math]\displaystyle{ C }[/math] in [math]\displaystyle{ G }[/math] with the smallest size [math]\displaystyle{ |C| }[/math].
Equivalently, the problem asks to find a bipartition of [math]\displaystyle{ V }[/math] into disjoint non-empty subsets [math]\displaystyle{ S }[/math] and [math]\displaystyle{ T }[/math] that minimizes [math]\displaystyle{ |E(S,T)| }[/math].
We consider the problem in a slightly more generalized setting, where the input graphs [math]\displaystyle{ G }[/math] can be multi-graphs, meaning that there could be multiple parallel edges between two vertices [math]\displaystyle{ u }[/math] and [math]\displaystyle{ v }[/math]. The cuts in multi-graphs are defined in the same way as before, and the cost of a cut [math]\displaystyle{ C }[/math] is given by the total number of edges (including parallel edges) in [math]\displaystyle{ C }[/math]. Equivalently, one may think of a multi-graph as a graph with integer edge weights, and the cost of a cut [math]\displaystyle{ C }[/math] is the total weights of all edges in [math]\displaystyle{ C }[/math].
A canonical deterministic algorithm for this problem is through the max-flow min-cut theorem. The max-flow algorithm finds us a minimum [math]\displaystyle{ s }[/math]-[math]\displaystyle{ t }[/math] cut, which disconnects a source [math]\displaystyle{ s\in V }[/math] from a sink [math]\displaystyle{ t\in V }[/math], both specified as part of the input. A global min cut can be found by exhaustively finding the minimum [math]\displaystyle{ s }[/math]-[math]\displaystyle{ t }[/math] cut for an arbitrarily fixed source [math]\displaystyle{ s }[/math] and all possible sink [math]\displaystyle{ t\neq s }[/math].
Karger's Algorithm
We will describe a simple and elegant randomized algorithm for the min-cut problem. The algorithm is due to David Karger.
Let [math]\displaystyle{ G(V, E) }[/math] be a multi-graph, which allows more than one parallel edges between two distinct vertices [math]\displaystyle{ u }[/math] and [math]\displaystyle{ v }[/math] but does not allow any self-loops: the edges that adjoin a vertex to itself. A multi-graph [math]\displaystyle{ G }[/math] can be represented by an adjacency matrix [math]\displaystyle{ A }[/math], in the way that each non-diagonal entry [math]\displaystyle{ A(u,v) }[/math] takes nonnegative integer values instead of just 0 or 1, representing the number of parallel edges between [math]\displaystyle{ u }[/math] and [math]\displaystyle{ v }[/math] in [math]\displaystyle{ G }[/math], and all diagonal entries [math]\displaystyle{ A(v,v)=0 }[/math] (since there is no self-loop).
Given a multi-graph [math]\displaystyle{ G(V,E) }[/math] and an edge [math]\displaystyle{ e\in E }[/math], we define the following contraction operator Contract([math]\displaystyle{ G }[/math], [math]\displaystyle{ e }[/math]), which transform [math]\displaystyle{ G }[/math] to a new multi-graph.
The contraction operator Contract([math]\displaystyle{ G }[/math], [math]\displaystyle{ e }[/math]) - say [math]\displaystyle{ e=uv }[/math]:
- replace [math]\displaystyle{ \{u,v\} }[/math] by a new vertex [math]\displaystyle{ x }[/math];
- for every edge (no matter parallel or not) in the form of [math]\displaystyle{ uw }[/math] or [math]\displaystyle{ vw }[/math] that connects one of [math]\displaystyle{ \{u,v\} }[/math] to a vertex [math]\displaystyle{ w\in V\setminus\{u,v\} }[/math] in the graph other than [math]\displaystyle{ u,v }[/math], replace it by a new edge [math]\displaystyle{ xw }[/math];
- the reset of the graph does not change.
- say [math]\displaystyle{ e=uv }[/math]:
In other words, the [math]\displaystyle{ Contract(G,uv) }[/math] merges the two vertices [math]\displaystyle{ u }[/math] and [math]\displaystyle{ v }[/math] into a new vertex [math]\displaystyle{ x }[/math] whose incident edges preserves the edges incident to [math]\displaystyle{ u }[/math] or [math]\displaystyle{ v }[/math] in the original graph [math]\displaystyle{ G }[/math] except for the parallel edges between them. Now you should realize why we consider multi-graphs instead of simple graphs, because even if we start with a simple graph without parallel edges, the contraction operator may create parallel edges.
The contraction operator is illustrated by the following picture:
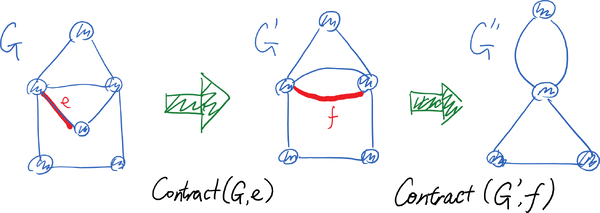
Karger's algorithm uses a simple idea:
- At each step we randomly select an edge in the current multi-graph to contract until there are only two vertices left.
- The parallel edges between these two remaining vertices must be a cut of the original graph.
- We return this cut and hope that with good chance this gives us a minimum cut.
The following is the pseudocode for Karger's algorithm.
RandomContract (Karger 1993) - Input: multi-graph [math]\displaystyle{ G(V,E) }[/math];
- while [math]\displaystyle{ |V|\gt 2 }[/math] do
- choose an edge [math]\displaystyle{ uv\in E }[/math] uniformly at random;
- [math]\displaystyle{ G=Contract(G,uv) }[/math];
- return [math]\displaystyle{ C=E }[/math] (the parallel edges between the only two vertices in [math]\displaystyle{ V }[/math]);
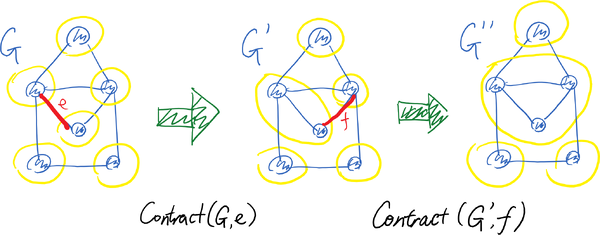
Another way of looking at the contraction operator Contract([math]\displaystyle{ G }[/math],[math]\displaystyle{ e }[/math]) is that it unions two classes of vertices. Let [math]\displaystyle{ V=\{v_1,v_2,\ldots,v_n\} }[/math] be the set of all vertices. We start with [math]\displaystyle{ n }[/math] vertex classes [math]\displaystyle{ S_1,S_2,\ldots, S_n }[/math] with each class [math]\displaystyle{ S_i=\{v_i\} }[/math] contains one vertex. By calling [math]\displaystyle{ Contract(G,uv) }[/math], where [math]\displaystyle{ u\in S_i }[/math] and [math]\displaystyle{ v\in S_j }[/math] for distinct [math]\displaystyle{ i\neq j }[/math], we take union of [math]\displaystyle{ S_i }[/math] and [math]\displaystyle{ S_j }[/math]. The edges in the contracted multi-graph are the edges that cross between different vertex classes.
This view of contraction is illustrated by the following picture:
Analysis of Karger's Algorithm
We now analyze the above algorithm. Since the algorithm is randomized, its output cut is random even when the input is fixed, so the output may not always be correct. We want to give a theoretical guarantee of the chance that the algorithm returns a correct answer on an arbitrary input.
More precisely, on an arbitrarily fixed input multi-graph [math]\displaystyle{ G }[/math], we want to answer the following question rigorously:
- [math]\displaystyle{ p_{\text{correct}}=\Pr[\,\text{a minimum cut is returned by }RandomContract\,]\ge ? }[/math]
To answer this question, we prove a stronger statement: for arbitrarily fixed input multi-graph [math]\displaystyle{ G }[/math] and a particular minimum cut [math]\displaystyle{ C }[/math] in [math]\displaystyle{ G }[/math],
- [math]\displaystyle{ p_{C}=\Pr[\,C\mbox{ is returned by }RandomContract\,]\ge ? }[/math]
Obviously this will imply the previous lower bound for [math]\displaystyle{ p_{\text{correct}} }[/math] because the event in [math]\displaystyle{ p_{C} }[/math] implies the event in [math]\displaystyle{ p_{\text{correct}} }[/math].
- In above argument we use the simple law in probability that [math]\displaystyle{ \Pr(A)\le \Pr(B) }[/math] if [math]\displaystyle{ A\subseteq B }[/math], i.e. event [math]\displaystyle{ A }[/math] implies event [math]\displaystyle{ B }[/math].
We introduce the following notations:
- Let [math]\displaystyle{ e_1,e_2,\ldots,e_{n-2} }[/math] denote the sequence of random edges chosen to contract in a running of RandomContract algorithm.
- Let [math]\displaystyle{ G_1=G }[/math] denote the original input multi-graph. And for [math]\displaystyle{ i=1,2,\ldots,n-2 }[/math], let [math]\displaystyle{ G_{i+1}=Contract(G_{i},e_i) }[/math] be the multigraph after [math]\displaystyle{ i }[/math]th contraction.
Obviously [math]\displaystyle{ e_1,e_2,\ldots,e_{n-2} }[/math] are random, and they are the only random choices used in the algorithm: meaning that they along with the input [math]\displaystyle{ G }[/math], uniquely determine the sequence of multi-graphs [math]\displaystyle{ G_1,G_2,\ldots,G_{n-2} }[/math] in every iteration as well as the final output.
We now compute the probability [math]\displaystyle{ p_C }[/math] by decompose it into more elementary events involving [math]\displaystyle{ e_1,e_2,\ldots,e_{n-2} }[/math]. This is due to the following proposition.
Proposition 1 - If [math]\displaystyle{ C }[/math] is a minimum cut in a multi-graph [math]\displaystyle{ G }[/math] and [math]\displaystyle{ e\not\in C }[/math], then [math]\displaystyle{ C }[/math] is still a minimum cut in the contracted graph [math]\displaystyle{ G'=contract(G,e) }[/math].
Proof. We first observe that contraction will never create new cuts: every cut in the contracted graph [math]\displaystyle{ G' }[/math] must also be a cut in the original graph [math]\displaystyle{ G }[/math].
We then observe that a cut [math]\displaystyle{ C }[/math] in [math]\displaystyle{ G }[/math] "survives" in the contracted graph [math]\displaystyle{ G' }[/math] if and only if the contracted edge [math]\displaystyle{ e\not\in C }[/math].
Both observations are easy to verify by the definition of contraction operator (in particular, easier to verify if we take the vertex class interpretation).
- [math]\displaystyle{ \square }[/math]
Recall that [math]\displaystyle{ e_1,e_2,\ldots,e_{n-2} }[/math] denote the sequence of random edges chosen to contract in a running of RandomContract algorithm.
By Proposition 1, the event [math]\displaystyle{ \mbox{``}C\mbox{ is returned by }RandomContract\mbox{''}\, }[/math] is equivalent to the event [math]\displaystyle{ \mbox{``}e_i\not\in C\mbox{ for all }i=1,2,\ldots,n-2\mbox{''} }[/math]. Therefore:
- [math]\displaystyle{ \begin{align} p_C &= \Pr[\,C\mbox{ is returned by }{RandomContract}\,]\\ &= \Pr[\,e_i\not\in C\mbox{ for all }i=1,2,\ldots,n-2\,]\\ &= \prod_{i=1}^{n-2}\Pr[e_i\not\in C\mid \forall j\lt i, e_j\not\in C]. \end{align} }[/math]
The last equation is due to the chain rule.
Now our task is to give lower bound to each [math]\displaystyle{ p_i=\Pr[e_i\not\in C\mid \forall j\lt i, e_j\not\in C] }[/math]. The condition [math]\displaystyle{ \mbox{``}\forall j\lt i, e_j\not\in C\mbox{''} }[/math] means the min-cut [math]\displaystyle{ C }[/math] survives all first [math]\displaystyle{ i-1 }[/math] contractions [math]\displaystyle{ e_1,e_2,\ldots,e_{i-1} }[/math], which due to Proposition 1 means that [math]\displaystyle{ C }[/math] is also a min-cut in the multi-graph [math]\displaystyle{ G_i }[/math] obtained from applying the first [math]\displaystyle{ (i-1) }[/math] contractions.
Then the conditional probability [math]\displaystyle{ p_i=\Pr[e_i\not\in C\mid \forall j\lt i, e_j\not\in C] }[/math] is the probability that no edge in [math]\displaystyle{ C }[/math] is hit when a uniform random edge in the current multi-graph is chosen assuming that [math]\displaystyle{ C }[/math] is a minimum cut in the current multi-graph. Intuitively this probability should be bounded from below, because as a min-cut [math]\displaystyle{ C }[/math] should be sparse among all edges. This intuition is justified by the following proposition.
Proposition 2 - If [math]\displaystyle{ C }[/math] is a min-cut in a multi-graph [math]\displaystyle{ G(V,E) }[/math], then [math]\displaystyle{ |E|\ge \frac{|V||C|}{2} }[/math].
Proof. - It must hold that the degree of each vertex [math]\displaystyle{ v\in V }[/math] is at least [math]\displaystyle{ |C| }[/math], or otherwise the set of edges incident to [math]\displaystyle{ v }[/math] forms a cut of size smaller than [math]\displaystyle{ |C| }[/math] which separates [math]\displaystyle{ \{v\} }[/math] from the rest of the graph, contradicting that [math]\displaystyle{ C }[/math] is a min-cut. And the bound [math]\displaystyle{ |E|\ge \frac{|V||C|}{2} }[/math] follows directly from applying the handshaking lemma to the fact that every vertex in [math]\displaystyle{ G }[/math] has degree at least [math]\displaystyle{ |C| }[/math].
- [math]\displaystyle{ \square }[/math]
Let [math]\displaystyle{ V_i }[/math] and [math]\displaystyle{ E_i }[/math] denote the vertex set and edge set of the multi-graph [math]\displaystyle{ G_i }[/math] respectively, and recall that [math]\displaystyle{ G_i }[/math] is the multi-graph obtained from applying first [math]\displaystyle{ (i-1) }[/math] contractions. Obviously [math]\displaystyle{ |V_{i}|=n-i+1 }[/math]. And due to Proposition 2, [math]\displaystyle{ |E_i|\ge \frac{|V_i||C|}{2} }[/math] if [math]\displaystyle{ C }[/math] is still a min-cut in [math]\displaystyle{ G_i }[/math].
The probability [math]\displaystyle{ p_i=\Pr[e_i\not\in C\mid \forall j\lt i, e_j\not\in C] }[/math] can be computed as
- [math]\displaystyle{ \begin{align} p_i &=1-\frac{|C|}{|E_i|}\\ &\ge1-\frac{2}{|V_i|}\\ &=1-\frac{2}{n-i+1} \end{align}, }[/math]
where the inequality is due to Proposition 2.
We now can put everything together. We arbitrarily fix the input multi-graph [math]\displaystyle{ G }[/math] and any particular minimum cut [math]\displaystyle{ C }[/math] in [math]\displaystyle{ G }[/math].
- [math]\displaystyle{ \begin{align} p_{\text{correct}} &=\Pr[\,\text{a minimum cut is returned by }RandomContract\,]\\ &\ge \Pr[\,C\mbox{ is returned by }{RandomContract}\,]\\ &= \Pr[\,e_i\not\in C\mbox{ for all }i=1,2,\ldots,n-2\,]\\ &= \prod_{i=1}^{n-2}\Pr[e_i\not\in C\mid \forall j\lt i, e_j\not\in C]\\ &\ge \prod_{i=1}^{n-2}\left(1-\frac{2}{n-i+1}\right)\\ &= \prod_{k=3}^{n}\frac{k-2}{k}\\ &= \frac{2}{n(n-1)}. \end{align} }[/math]
This gives us the following theorem.
Theorem - For any multigraph with [math]\displaystyle{ n }[/math] vertices, the RandomContract algorithm returns a minimum cut with probability at least [math]\displaystyle{ \frac{2}{n(n-1)} }[/math].
At first glance this seems to be a quite slim chance of success. However, notice that there may be exponential many cuts in a graph (because potentially every nonempty subset [math]\displaystyle{ S\subset V }[/math] corresponds to a cut [math]\displaystyle{ C=E(S,\overline{S}) }[/math]), and Karger's algorithm effectively reduce this exponential-sized space to quadratic-sized, an exponential improvement!
We can run RandomContract independently for [math]\displaystyle{ t=\left\lceil\frac{n(n-1)\ln n}{2}\right\rceil }[/math] times and return the smallest cut ever returned. The probability that a minimum cut is found is at least:
- [math]\displaystyle{ \begin{align} &\quad 1-\Pr[\,\mbox{all }t\mbox{ independent runnings of } RandomContract\mbox{ fails to find a min-cut}\,] \\ &= 1-\Pr[\,\mbox{a single running of }{RandomContract}\mbox{ fails}\,]^{t} \\ &\ge 1- \left(1-\frac{2}{n(n-1)}\right)^{\frac{n(n-1)\ln n}{2}} \\ &\ge 1-\frac{1}{n}. \end{align} }[/math]
A Consequence of the Probabilistic Method
The analysis of Karger's algorithm implies the following combinatorial proposition for the number of distinct minimum cuts in a graph.
Corollary - For any graph [math]\displaystyle{ G(V,E) }[/math] of [math]\displaystyle{ n }[/math] vertices, the number of distinct minimum cuts in [math]\displaystyle{ G }[/math] is at most [math]\displaystyle{ \frac{n(n-1)}{2} }[/math].
Proof. Let [math]\displaystyle{ \mathcal{C} }[/math] denote the set of all minimum cuts in [math]\displaystyle{ G }[/math]. For each min-cut [math]\displaystyle{ C\in\mathcal{C} }[/math], let [math]\displaystyle{ A_C }[/math] denote the event "[math]\displaystyle{ C }[/math] is returned by RandomContract", whose probability is given by
- [math]\displaystyle{ p_C=\Pr(A_C)\, }[/math].
Clearly we have:
- for any distinct [math]\displaystyle{ C,D\in\mathcal{C} }[/math], [math]\displaystyle{ A_C\, }[/math] and [math]\displaystyle{ A_{D}\, }[/math] are disjoint events; and
- the union [math]\displaystyle{ \bigcup_{C\in\mathcal{C}}A_C }[/math] is precisely the event "a minimum cut is returned by RandomContract", whose probability is given by
- [math]\displaystyle{ p_{\text{correct}}=\Pr[\,\text{a minimum cut is returned by } RandomContract\,] }[/math].
Due to the additivity of probability, it holds that
- [math]\displaystyle{ p_{\text{correct}}=\sum_{C\in\mathcal{C}}\Pr(A_C)=\sum_{C\in\mathcal{C}}p_C. }[/math]
By the analysis of Karger's algorithm, we know [math]\displaystyle{ p_C\ge\frac{2}{n(n-1)} }[/math]. And since [math]\displaystyle{ p_{\text{correct}} }[/math] is a well defined probability, due to the unitarity of probability, it must hold that [math]\displaystyle{ p_{\text{correct}}\le 1 }[/math]. Therefore,
- [math]\displaystyle{ 1\ge p_{\text{correct}}=\sum_{C\in\mathcal{C}}p_C\ge|\mathcal{C}|\frac{2}{n(n-1)} }[/math],
which means [math]\displaystyle{ |\mathcal{C}|\le\frac{n(n-1)}{2} }[/math].
- [math]\displaystyle{ \square }[/math]
Note that the statement of this theorem has no randomness at all, while the proof consists of a randomized procedure. This is an example of the probabilistic method.