随机算法 (Spring 2014)/Universal Hashing
[math]\displaystyle{ k }[/math]-wise independence
Recall the definition of independence between events:
Definition (Independent events) - Events [math]\displaystyle{ \mathcal{E}_1, \mathcal{E}_2, \ldots, \mathcal{E}_n }[/math] are mutually independent if, for any subset [math]\displaystyle{ I\subseteq\{1,2,\ldots,n\} }[/math],
- [math]\displaystyle{ \begin{align} \Pr\left[\bigwedge_{i\in I}\mathcal{E}_i\right] &= \prod_{i\in I}\Pr[\mathcal{E}_i]. \end{align} }[/math]
- Events [math]\displaystyle{ \mathcal{E}_1, \mathcal{E}_2, \ldots, \mathcal{E}_n }[/math] are mutually independent if, for any subset [math]\displaystyle{ I\subseteq\{1,2,\ldots,n\} }[/math],
Similarly, we can define independence between random variables:
Definition (Independent variables) - Random variables [math]\displaystyle{ X_1, X_2, \ldots, X_n }[/math] are mutually independent if, for any subset [math]\displaystyle{ I\subseteq\{1,2,\ldots,n\} }[/math] and any values [math]\displaystyle{ x_i }[/math], where [math]\displaystyle{ i\in I }[/math],
- [math]\displaystyle{ \begin{align} \Pr\left[\bigwedge_{i\in I}(X_i=x_i)\right] &= \prod_{i\in I}\Pr[X_i=x_i]. \end{align} }[/math]
- Random variables [math]\displaystyle{ X_1, X_2, \ldots, X_n }[/math] are mutually independent if, for any subset [math]\displaystyle{ I\subseteq\{1,2,\ldots,n\} }[/math] and any values [math]\displaystyle{ x_i }[/math], where [math]\displaystyle{ i\in I }[/math],
Mutual independence is an ideal condition of independence. The limited notion of independence is usually defined by the k-wise independence.
Definition (k-wise Independenc) - 1. Events [math]\displaystyle{ \mathcal{E}_1, \mathcal{E}_2, \ldots, \mathcal{E}_n }[/math] are k-wise independent if, for any subset [math]\displaystyle{ I\subseteq\{1,2,\ldots,n\} }[/math] with [math]\displaystyle{ |I|\le k }[/math]
- [math]\displaystyle{ \begin{align} \Pr\left[\bigwedge_{i\in I}\mathcal{E}_i\right] &= \prod_{i\in I}\Pr[\mathcal{E}_i]. \end{align} }[/math]
- 2. Random variables [math]\displaystyle{ X_1, X_2, \ldots, X_n }[/math] are k-wise independent if, for any subset [math]\displaystyle{ I\subseteq\{1,2,\ldots,n\} }[/math] with [math]\displaystyle{ |I|\le k }[/math] and any values [math]\displaystyle{ x_i }[/math], where [math]\displaystyle{ i\in I }[/math],
- [math]\displaystyle{ \begin{align} \Pr\left[\bigwedge_{i\in I}(X_i=x_i)\right] &= \prod_{i\in I}\Pr[X_i=x_i]. \end{align} }[/math]
- 1. Events [math]\displaystyle{ \mathcal{E}_1, \mathcal{E}_2, \ldots, \mathcal{E}_n }[/math] are k-wise independent if, for any subset [math]\displaystyle{ I\subseteq\{1,2,\ldots,n\} }[/math] with [math]\displaystyle{ |I|\le k }[/math]
A very common case is pairwise independence, i.e. the 2-wise independence.
Definition (pairwise Independent random variables) - Random variables [math]\displaystyle{ X_1, X_2, \ldots, X_n }[/math] are pairwise independent if, for any [math]\displaystyle{ X_i,X_j }[/math] where [math]\displaystyle{ i\neq j }[/math] and any values [math]\displaystyle{ a,b }[/math]
- [math]\displaystyle{ \begin{align} \Pr\left[X_i=a\wedge X_j=b\right] &= \Pr[X_i=a]\cdot\Pr[X_j=b]. \end{align} }[/math]
- Random variables [math]\displaystyle{ X_1, X_2, \ldots, X_n }[/math] are pairwise independent if, for any [math]\displaystyle{ X_i,X_j }[/math] where [math]\displaystyle{ i\neq j }[/math] and any values [math]\displaystyle{ a,b }[/math]
Note that the definition of k-wise independence is hereditary:
- If [math]\displaystyle{ X_1, X_2, \ldots, X_n }[/math] are k-wise independent, then they are also [math]\displaystyle{ \ell }[/math]-wise independent for any [math]\displaystyle{ \ell\lt k }[/math].
- If [math]\displaystyle{ X_1, X_2, \ldots, X_n }[/math] are NOT k-wise independent, then they cannot be [math]\displaystyle{ \ell }[/math]-wise independent for any [math]\displaystyle{ \ell\gt k }[/math].
Pairwise Independent Bits
Suppose we have [math]\displaystyle{ m }[/math] mutually independent and uniform random bits [math]\displaystyle{ X_1,\ldots, X_m }[/math]. We are going to extract [math]\displaystyle{ n=2^m-1 }[/math] pairwise independent bits from these [math]\displaystyle{ m }[/math] mutually independent bits.
Enumerate all the nonempty subsets of [math]\displaystyle{ \{1,2,\ldots,m\} }[/math] in some order. Let [math]\displaystyle{ S_j }[/math] be the [math]\displaystyle{ j }[/math]th subset. Let
- [math]\displaystyle{ Y_j=\bigoplus_{i\in S_j} X_i, }[/math]
where [math]\displaystyle{ \oplus }[/math] is the exclusive-or, whose truth table is as follows.
[math]\displaystyle{ a }[/math] [math]\displaystyle{ b }[/math] [math]\displaystyle{ a }[/math][math]\displaystyle{ \oplus }[/math][math]\displaystyle{ b }[/math] 0 0 0 0 1 1 1 0 1 1 1 0
There are [math]\displaystyle{ n=2^m-1 }[/math] such [math]\displaystyle{ Y_j }[/math], because there are [math]\displaystyle{ 2^m-1 }[/math] nonempty subsets of [math]\displaystyle{ \{1,2,\ldots,m\} }[/math]. An equivalent definition of [math]\displaystyle{ Y_j }[/math] is
- [math]\displaystyle{ Y_j=\left(\sum_{i\in S_j}X_i\right)\bmod 2 }[/math].
Sometimes, [math]\displaystyle{ Y_j }[/math] is called the parity of the bits in [math]\displaystyle{ S_j }[/math].
We claim that [math]\displaystyle{ Y_j }[/math] are pairwise independent and uniform.
Theorem - For any [math]\displaystyle{ Y_j }[/math] and any [math]\displaystyle{ b\in\{0,1\} }[/math],
- [math]\displaystyle{ \begin{align} \Pr\left[Y_j=b\right] &= \frac{1}{2}. \end{align} }[/math]
- For any [math]\displaystyle{ Y_j,Y_\ell }[/math] that [math]\displaystyle{ j\neq\ell }[/math] and any [math]\displaystyle{ a,b\in\{0,1\} }[/math],
- [math]\displaystyle{ \begin{align} \Pr\left[Y_j=a\wedge Y_\ell=b\right] &= \frac{1}{4}. \end{align} }[/math]
- For any [math]\displaystyle{ Y_j }[/math] and any [math]\displaystyle{ b\in\{0,1\} }[/math],
The proof is left for your exercise.
Therefore, we extract exponentially many pairwise independent uniform random bits from a sequence of mutually independent uniform random bits.
Note that [math]\displaystyle{ Y_j }[/math] are not 3-wise independent. For example, consider the subsets [math]\displaystyle{ S_1=\{1\},S_2=\{2\},S_3=\{1,2\} }[/math] and the corresponding random bits [math]\displaystyle{ Y_1,Y_2,Y_3 }[/math]. Any two of [math]\displaystyle{ Y_1,Y_2,Y_3 }[/math] would decide the value of the third one.
Pairwise Independent Variables
We now consider constructing pairwise independent random variables ranging over [math]\displaystyle{ [p]=\{0,1,2,\ldots,p-1\} }[/math] for some prime [math]\displaystyle{ p }[/math]. Unlike the above construction, now we only need two independent random sources [math]\displaystyle{ X_0,X_1 }[/math], which are uniformly and independently distributed over [math]\displaystyle{ [p] }[/math].
Let [math]\displaystyle{ Y_0,Y_1,\ldots, Y_{p-1} }[/math] be defined as:
- [math]\displaystyle{ \begin{align} Y_i=(X_0+i\cdot X_1)\bmod p &\quad \mbox{for }i\in[p]. \end{align} }[/math]
Theorem - The random variables [math]\displaystyle{ Y_0,Y_1,\ldots, Y_{p-1} }[/math] are pairwise independent uniform random variables over [math]\displaystyle{ [p] }[/math].
Proof. We first show that [math]\displaystyle{ Y_i }[/math] are uniform. That is, we will show that for any [math]\displaystyle{ i,a\in[p] }[/math], - [math]\displaystyle{ \begin{align} \Pr\left[(X_0+i\cdot X_1)\bmod p=a\right] &= \frac{1}{p}. \end{align} }[/math]
Due to the law of total probability,
- [math]\displaystyle{ \begin{align} \Pr\left[(X_0+i\cdot X_1)\bmod p=a\right] &= \sum_{j\in[p]}\Pr[X_1=j]\cdot\Pr\left[(X_0+ij)\bmod p=a\right]\\ &=\frac{1}{p}\sum_{j\in[p]}\Pr\left[X_0\equiv(a-ij)\pmod{p}\right]. \end{align} }[/math]
For prime [math]\displaystyle{ p }[/math], for any [math]\displaystyle{ i,j,a\in[p] }[/math], there is exact one value in [math]\displaystyle{ [p] }[/math] of [math]\displaystyle{ X_0 }[/math] satisfying [math]\displaystyle{ X_0\equiv(a-ij)\pmod{p} }[/math]. Thus, [math]\displaystyle{ \Pr\left[X_0\equiv(a-ij)\pmod{p}\right]=1/p }[/math] and the above probability is [math]\displaystyle{ \frac{1}{p} }[/math].
We then show that [math]\displaystyle{ Y_i }[/math] are pairwise independent, i.e. we will show that for any [math]\displaystyle{ Y_i,Y_j }[/math] that [math]\displaystyle{ i\neq j }[/math] and any [math]\displaystyle{ a,b\in[p] }[/math],
- [math]\displaystyle{ \begin{align} \Pr\left[Y_i=a\wedge Y_j=b\right] &= \frac{1}{p^2}. \end{align} }[/math]
The event [math]\displaystyle{ Y_i=a\wedge Y_j=b }[/math] is equivalent to that
- [math]\displaystyle{ \begin{cases} (X_0+iX_1)\equiv a\pmod{p}\\ (X_0+jX_1)\equiv b\pmod{p} \end{cases} }[/math]
Due to the Chinese remainder theorem, there exists a unique solution of [math]\displaystyle{ X_0 }[/math] and [math]\displaystyle{ X_1 }[/math] in [math]\displaystyle{ [p] }[/math] to the above linear congruential system. Thus the probability of the event is [math]\displaystyle{ \frac{1}{p^2} }[/math].
- [math]\displaystyle{ \square }[/math]
Application: Derandomizing MAX-CUT
Let [math]\displaystyle{ G(V,E) }[/math] be an undirected graph, and [math]\displaystyle{ S\subset V }[/math] be a vertex set. The cut defined by [math]\displaystyle{ S }[/math] is [math]\displaystyle{ C(S,\bar{S})=|\{uv\in E\mid u\in S, v\not\in S\}| }[/math].
Given as input an undirected graph [math]\displaystyle{ G(V,E) }[/math], find the [math]\displaystyle{ S\subset V }[/math] whose cut value [math]\displaystyle{ C(S,\bar{S}) }[/math] is maximized. This problem is called the maximum cut (MAX-CUT) problem, which is NP-hard. The decision version of one of the weighted version of the problem is one of the Karp's 21 NP-complete problems. The problem has a [math]\displaystyle{ 0.878 }[/math]-approximation algorithm by rounding a semidefinite programming. Assuming that the unique game conjecture (UGC), there does not exist a poly-time algorithm with better approximation ratio unless [math]\displaystyle{ P=NP }[/math].
Here we give a very simple [math]\displaystyle{ 0.5 }[/math]-approximation algorithm. The "algorithm" has a one-line description:
- Put each [math]\displaystyle{ v\in V }[/math] into [math]\displaystyle{ S }[/math] independently with probability 1/2.
We then analyze the approximation ratio of this algorithm.
For each [math]\displaystyle{ v\in V }[/math], let [math]\displaystyle{ Y_v }[/math] indicate whether [math]\displaystyle{ v\in S }[/math], that is
- [math]\displaystyle{ Y_v=\begin{cases}1& v\in S,\\ 0& v\not\in S.\end{cases} }[/math]
For each edge [math]\displaystyle{ uv\in E }[/math], let [math]\displaystyle{ Y_{uv} }[/math] indicate whether [math]\displaystyle{ uv }[/math] contribute to the cut [math]\displaystyle{ C(S,\bar{S}) }[/math], i.e. whether [math]\displaystyle{ u\in S, v\not\in S }[/math] or [math]\displaystyle{ u\not\in S, v\in S }[/math], that is
- [math]\displaystyle{ Y_{uv}=\begin{cases}1&Y_u\neq Y_v,\\0&\text{otherwise}.\end{cases} }[/math]
Then [math]\displaystyle{ C(S,\bar{S})=\sum_{uv\in E}Y_{uv} }[/math]. Due to the linearity of expectation,
- [math]\displaystyle{ \mathbf{E}\left[C(S,\bar{S})\right]=\sum_{uv\in E}\mathbf{E}[Y_{uv}]=\sum_{uv\in E}\Pr[Y_u\neq Y_v]=\frac{|E|}{2} }[/math].
The maximum cut of a graph is at most [math]\displaystyle{ |E| }[/math]. Thus, the algorithm returns in expectation a cut with size at least half of the maximum cut.
We then show how to dereandomize this algorithm by pairwise independent bits.
Suppose that [math]\displaystyle{ |V|=n }[/math] and enumerate the [math]\displaystyle{ n }[/math] vertices by [math]\displaystyle{ v_1,v_2,\ldots, v_n }[/math] in an arbitrary order. Let [math]\displaystyle{ m=\lceil\log_2 (n+1)\rceil }[/math]. Sample [math]\displaystyle{ m }[/math] bits [math]\displaystyle{ X_1,\ldots, X_m\in\{0,1\} }[/math] uniformly and independently at random. Enumerate all nonempty subsets of [math]\displaystyle{ \{1,2,\ldots,m\} }[/math] by [math]\displaystyle{ S_1,S_2,\ldots,S_{2^m-1} }[/math]. For each vertex [math]\displaystyle{ v_j }[/math], let [math]\displaystyle{ Y_{v_j}=\bigoplus_{i\in S_j}X_i }[/math]. The MAX-CUT algorithm uses these bits to construct the solution [math]\displaystyle{ S }[/math]:
- For [math]\displaystyle{ j=1,2,\ldots,n }[/math], put [math]\displaystyle{ v_j }[/math] into [math]\displaystyle{ S }[/math] if [math]\displaystyle{ Y_{v_j}=1 }[/math].
We have shown that [math]\displaystyle{ Y_{v_j} }[/math], [math]\displaystyle{ j=1,2,\ldots,n }[/math], are uniform and pairwise independent. Thus we still have that [math]\displaystyle{ \Pr[Y_{u}\neq Y_{v}]=\frac{1}{2} }[/math]. The above analysis still holds, so that the algorithm returns in expectation a cut with size at least [math]\displaystyle{ \frac{|E|}{2} }[/math].
Finally, we notice that there are only [math]\displaystyle{ m=\lceil\log_2 (n+1)\rceil }[/math] total random bits in the new algorithm. We can enumerate all [math]\displaystyle{ 2^m\le 2(n+1) }[/math] possible strings of [math]\displaystyle{ m }[/math] bits, run the above algorithm with the bit strings as the "random sources", and output the maximum cut returned. There must exist a bit string [math]\displaystyle{ X_1,\ldots, X_m\in\{0,1\} }[/math] on which the algorithm returns a cut of size [math]\displaystyle{ \ge \frac{|E|}{2} }[/math] (why?). This gives us a deterministic polynomial time (actually [math]\displaystyle{ O(n^2) }[/math] time) [math]\displaystyle{ 1/2 }[/math]-approximation algorithm.
Universal Hashing
Hashing is one of the oldest tools in Computer Science. Knuth's memorandum in 1963 on analysis of hash tables is now considered to be the birth of the area of analysis of algorithms.
- Knuth. Notes on "open" addressing, July 22 1963. Unpublished memorandum.
The idea of hashing is simple: an unknown set [math]\displaystyle{ S }[/math] of [math]\displaystyle{ n }[/math] data items (or keys) are drawn from a large universe [math]\displaystyle{ U=[N] }[/math] where [math]\displaystyle{ N\gg n }[/math]; in order to store [math]\displaystyle{ S }[/math] in a table of [math]\displaystyle{ M }[/math] entries (slots), we assume a consistent mapping (called a hash function) from the universe [math]\displaystyle{ U }[/math] to a small range [math]\displaystyle{ [M] }[/math].
This idea seems clever: we use a consistent mapping to deal with an arbitrary unknown data set. However, there is a fundamental flaw for hashing.
- For sufficiently large universe ([math]\displaystyle{ N\gt M(n-1) }[/math]), for any function, there exists a bad data set [math]\displaystyle{ S }[/math], such that all items in [math]\displaystyle{ S }[/math] are mapped to the same entry in the table.
A simple use of pigeonhole principle can prove the above statement.
To overcome this situation, randomization is introduced into hashing. We assume that the hash function is a random mapping from [math]\displaystyle{ [N] }[/math] to [math]\displaystyle{ [M] }[/math]. In order to ease the analysis, the following ideal assumption is used:
Simple Uniform Hash Assumption (SUHA or UHA, a.k.a. the random oracle model):
- A uniform random function [math]\displaystyle{ h:[N]\rightarrow[M] }[/math] is available and the computation of [math]\displaystyle{ h }[/math] is efficient.
Families of universal hash functions
The assumption of completely random function simplifies the analysis. However, in practice, truly uniform random hash function is extremely expensive to compute and store. Thus, this simple assumption can hardly represent the reality.
There are two approaches for implementing practical hash functions. One is to use ad hoc implementations and wish they may work. The other approach is to construct class of hash functions which are efficient to compute and store but with weaker randomness guarantees, and then analyze the applications of hash functions based on this weaker assumption of randomness.
This route was took by Carter and Wegman in 1977 while they introduced universal families of hash functions.
Definition (universal hash families) - Let [math]\displaystyle{ [N] }[/math] be a universe with [math]\displaystyle{ N\ge M }[/math]. A family of hash functions [math]\displaystyle{ \mathcal{H} }[/math] from [math]\displaystyle{ [N] }[/math] to [math]\displaystyle{ [M] }[/math] is said to be [math]\displaystyle{ k }[/math]-universal if, for any items [math]\displaystyle{ x_1,x_2,\ldots,x_k\in [N] }[/math] and for a hash function [math]\displaystyle{ h }[/math] chosen uniformly at random from [math]\displaystyle{ \mathcal{H} }[/math], we have
- [math]\displaystyle{ \Pr[h(x_1)=h(x_2)=\cdots=h(x_k)]\le\frac{1}{M^{k-1}}. }[/math]
- A family of hash functions [math]\displaystyle{ \mathcal{H} }[/math] from [math]\displaystyle{ [N] }[/math] to [math]\displaystyle{ [M] }[/math] is said to be strongly [math]\displaystyle{ k }[/math]-universal if, for any items [math]\displaystyle{ x_1,x_2,\ldots,x_k\in [N] }[/math], any values [math]\displaystyle{ y_1,y_2,\ldots,y_k\in[M] }[/math], and for a hash function [math]\displaystyle{ h }[/math] chosen uniformly at random from [math]\displaystyle{ \mathcal{H} }[/math], we have
- [math]\displaystyle{ \Pr[h(x_1)=y_1\wedge h(x_2)=y_2 \wedge \cdots \wedge h(x_k)=y_k]=\frac{1}{M^{k}}. }[/math]
- Let [math]\displaystyle{ [N] }[/math] be a universe with [math]\displaystyle{ N\ge M }[/math]. A family of hash functions [math]\displaystyle{ \mathcal{H} }[/math] from [math]\displaystyle{ [N] }[/math] to [math]\displaystyle{ [M] }[/math] is said to be [math]\displaystyle{ k }[/math]-universal if, for any items [math]\displaystyle{ x_1,x_2,\ldots,x_k\in [N] }[/math] and for a hash function [math]\displaystyle{ h }[/math] chosen uniformly at random from [math]\displaystyle{ \mathcal{H} }[/math], we have
In particular, for a 2-universal family [math]\displaystyle{ \mathcal{H} }[/math], for any elements [math]\displaystyle{ x_1,x_2\in[N] }[/math], a uniform random [math]\displaystyle{ h\in\mathcal{H} }[/math] has
- [math]\displaystyle{ \Pr[h(x_1)=h(x_2)]\le\frac{1}{M}. }[/math]
For a strongly 2-universal family [math]\displaystyle{ \mathcal{H} }[/math], for any elements [math]\displaystyle{ x_1,x_2\in[N] }[/math] and any values [math]\displaystyle{ y_1,y_2\in[M] }[/math], a uniform random [math]\displaystyle{ h\in\mathcal{H} }[/math] has
- [math]\displaystyle{ \Pr[h(x_1)=y_1\wedge h(x_2)=y_2]=\frac{1}{M^2}. }[/math]
This behavior is exactly the same as uniform random hash functions on any pair of inputs. For this reason, a strongly 2-universal hash family are also called pairwise independent hash functions.
2-universal hash families
The construction of pairwise independent random variables via modulo a prime introduced in Section 1 already provides a way of constructing a strongly 2-universal hash family.
Let [math]\displaystyle{ p }[/math] be a prime. The function [math]\displaystyle{ h_{a,b}:[p]\rightarrow [p] }[/math] is defined by
- [math]\displaystyle{ h_{a,b}(x)=(ax+b)\bmod p, }[/math]
and the family is
- [math]\displaystyle{ \mathcal{H}=\{h_{a,b}\mid a,b\in[p]\}. }[/math]
Lemma - [math]\displaystyle{ \mathcal{H} }[/math] is strongly 2-universal.
Proof. In Section 1, we have proved the pairwise independence of the sequence of [math]\displaystyle{ (a i+b)\bmod p }[/math], for [math]\displaystyle{ i=0,1,\ldots, p-1 }[/math], which directly implies that [math]\displaystyle{ \mathcal{H} }[/math] is strongly 2-universal.
- [math]\displaystyle{ \square }[/math]
- The original construction of Carter-Wegman
What if we want to have hash functions from [math]\displaystyle{ [N] }[/math] to [math]\displaystyle{ [M] }[/math] for non-prime [math]\displaystyle{ N }[/math] and [math]\displaystyle{ M }[/math]? Carter and Wegman developed the following method.
Suppose that the universe is [math]\displaystyle{ [N] }[/math], and the functions map [math]\displaystyle{ [N] }[/math] to [math]\displaystyle{ [M] }[/math], where [math]\displaystyle{ N\ge M }[/math]. For some prime [math]\displaystyle{ p\ge N }[/math], let
- [math]\displaystyle{ h_{a,b}(x)=((ax+b)\bmod p)\bmod M, }[/math]
and the family
- [math]\displaystyle{ \mathcal{H}=\{h_{a,b}\mid 1\le a\le p-1, b\in[p]\}. }[/math]
Note that unlike the first construction, now [math]\displaystyle{ a\neq 0 }[/math].
Lemma (Carter-Wegman) - [math]\displaystyle{ \mathcal{H} }[/math] is 2-universal.
Proof. Due to the definition of [math]\displaystyle{ \mathcal{H} }[/math], there are [math]\displaystyle{ p(p-1) }[/math] many different hash functions in [math]\displaystyle{ \mathcal{H} }[/math], because each hash function in [math]\displaystyle{ \mathcal{H} }[/math] corresponds to a pair of [math]\displaystyle{ 1\le a\le p-1 }[/math] and [math]\displaystyle{ b\in[p] }[/math]. We only need to count for any particular pair of [math]\displaystyle{ x_1,x_2\in[N] }[/math] that [math]\displaystyle{ x_1\neq x_2 }[/math], the number of hash functions that [math]\displaystyle{ h(x_1)=h(x_2) }[/math]. We first note that for any [math]\displaystyle{ x_1\neq x_2 }[/math], [math]\displaystyle{ a x_1+b\not\equiv a x_2+b \pmod p }[/math]. This is because [math]\displaystyle{ a x_1+b\equiv a x_2+b \pmod p }[/math] would imply that [math]\displaystyle{ a(x_1-x_2)\equiv 0\pmod p }[/math], which can never happen since [math]\displaystyle{ 1\le a\le p-1 }[/math] and [math]\displaystyle{ x_1\neq x_2 }[/math] (note that [math]\displaystyle{ x_1,x_2\in[N] }[/math] for an [math]\displaystyle{ N\le p }[/math]). Therefore, we can assume that [math]\displaystyle{ (a x_1+b)\bmod p=u }[/math] and [math]\displaystyle{ (a x_2+b)\bmod p=v }[/math] for [math]\displaystyle{ u\neq v }[/math].
Due to the Chinese remainder theorem, for any [math]\displaystyle{ x_1,x_2\in[N] }[/math] that [math]\displaystyle{ x_1\neq x_2 }[/math], for any [math]\displaystyle{ u,v\in[p] }[/math] that [math]\displaystyle{ u\neq v }[/math], there is exact one solution to [math]\displaystyle{ (a,b) }[/math] satisfying:
- [math]\displaystyle{ \begin{cases} a x_1+b \equiv u \pmod p\\ a x_2+b \equiv v \pmod p. \end{cases} }[/math]
After modulo [math]\displaystyle{ M }[/math], every [math]\displaystyle{ u\in[p] }[/math] has at most [math]\displaystyle{ \lceil p/M\rceil -1 }[/math] many [math]\displaystyle{ v\in[p] }[/math] that [math]\displaystyle{ v\neq u }[/math] but [math]\displaystyle{ v\equiv u\pmod M }[/math]. Therefore, for every pair of [math]\displaystyle{ x_1,x_2\in[N] }[/math] that [math]\displaystyle{ x_1\neq x_2 }[/math], there exist at most [math]\displaystyle{ p(\lceil p/M\rceil -1)\le p(p-1)/M }[/math] pairs of [math]\displaystyle{ 1\le a\le p-1 }[/math] and [math]\displaystyle{ b\in[p] }[/math] such that [math]\displaystyle{ ((ax_1+b)\bmod p)\bmod M=((ax_2+b)\bmod p)\bmod M }[/math], which means there are at most [math]\displaystyle{ p(p-1)/M }[/math] many hash functions [math]\displaystyle{ h\in\mathcal{H} }[/math] having [math]\displaystyle{ h(x_1)=h(x_2) }[/math] for [math]\displaystyle{ x_1\neq x_2 }[/math]. For [math]\displaystyle{ h }[/math] uniformly chosen from [math]\displaystyle{ \mathcal{H} }[/math], for any [math]\displaystyle{ x_1\neq x_2 }[/math],
- [math]\displaystyle{ \Pr[h(x_1)=h(x_2)]\le \frac{p(p-1)/M}{p(p-1)}=\frac{1}{M}. }[/math]
We prove that [math]\displaystyle{ \mathcal{H} }[/math] is 2-universal.
- [math]\displaystyle{ \square }[/math]
- A construction used in practice
The main issue of Carter-Wegman construction is the efficiency. The mod operation is very slow, and has been so for more than 30 years.
The following construction is due to Dietzfelbinger et al. It was published in 1997 and has been practically used in various applications of universal hashing.
The family of hash functions is from [math]\displaystyle{ [2^u] }[/math] to [math]\displaystyle{ [2^v] }[/math]. With a binary representation, the functions map binary strings of length [math]\displaystyle{ u }[/math] to binary strings of length [math]\displaystyle{ v }[/math]. Let
- [math]\displaystyle{ h_{a}(x)=\left\lfloor\frac{a\cdot x\bmod 2^u}{2^{u-v}}\right\rfloor, }[/math]
and the family
- [math]\displaystyle{ \mathcal{H}=\{h_{a}\mid a\in[2^v]\mbox{ and }a\mbox{ is odd}\}. }[/math]
This family of hash functions does not exactly meet the requirement of 2-universal family. However, Dietzfelbinger et al proved that [math]\displaystyle{ \mathcal{H} }[/math] is close to a 2-universal family. Specifically, for any input values [math]\displaystyle{ x_1,x_2\in[2^u] }[/math], for a uniformly random [math]\displaystyle{ h\in\mathcal{H} }[/math],
- [math]\displaystyle{ \Pr[h(x_1)=h(x_2)]\le\frac{1}{2^{v-1}}. }[/math]
So [math]\displaystyle{ \mathcal{H} }[/math] is within an approximation ratio of 2 to being 2-universal. The proof uses the fact that odd numbers are relative prime to a power of 2.
The function is extremely simple to compute in c language. We exploit that C-multiplication (*) of unsigned u-bit numbers is done [math]\displaystyle{ \bmod 2^u }[/math], and have a one-line C-code for computing the hash function:
h_a(x) = (a*x)>>(u-v)
The bit-wise shifting is a lot faster than modular. It explains the popularity of this scheme in practice than the original Carter-Wegman construction.
Collision number
Consider a 2-universal family [math]\displaystyle{ \mathcal{H} }[/math] of hash functions from [math]\displaystyle{ [N] }[/math] to [math]\displaystyle{ [M] }[/math]. Let [math]\displaystyle{ h }[/math] be a hash function chosen uniformly from [math]\displaystyle{ \mathcal{H} }[/math]. For a fixed set [math]\displaystyle{ S }[/math] of [math]\displaystyle{ n }[/math] distinct elements from [math]\displaystyle{ [N] }[/math], say [math]\displaystyle{ S=\{x_1,x_2,\ldots,x_n\} }[/math], the elements are mapped to the hash values [math]\displaystyle{ h(x_1), h(x_2), \ldots, h(x_n) }[/math]. This can be seen as throwing [math]\displaystyle{ n }[/math] balls to [math]\displaystyle{ M }[/math] bins, with pairwise independent choices of bins.
As in the balls-into-bins with full independence, we are curious about the questions such as the birthday problem or the maximum load. These questions are interesting not only because they are natural to ask in a balls-into-bins setting, but in the context of hashing, they are closely related to the performance of hash functions.
The old techniques for analyzing balls-into-bins rely too much on the independence of the choice of the bin for each ball, therefore can hardly be extended to the setting of 2-universal hash families. However, it turns out several balls-into-bins questions can somehow be answered by analyzing a very natural quantity: the number of collision pairs.
A collision pair for hashing is a pair of elements [math]\displaystyle{ x_1,x_2\in S }[/math] which are mapped to the same hash value, i.e. [math]\displaystyle{ h(x_1)=h(x_2) }[/math]. Formally, for a fixed set of elements [math]\displaystyle{ S=\{x_1,x_2,\ldots,x_n\} }[/math], for any [math]\displaystyle{ 1\le i,j\le n }[/math], let the random variable
- [math]\displaystyle{ X_{ij} = \begin{cases} 1 & \text{if }h(x_i)=h(x_j),\\ 0 & \text{otherwise.} \end{cases} }[/math]
The total number of collision pairs among the [math]\displaystyle{ n }[/math] items [math]\displaystyle{ x_1,x_2,\ldots,x_n }[/math] is
- [math]\displaystyle{ X=\sum_{i\lt j} X_{ij}.\, }[/math]
Since [math]\displaystyle{ \mathcal{H} }[/math] is 2-universal, for any [math]\displaystyle{ i\neq j }[/math],
- [math]\displaystyle{ \Pr[X_{ij}=1]=\Pr[h(x_i)=h(x_j)]\le\frac{1}{M}. }[/math]
The expected number of collision pairs is
- [math]\displaystyle{ \mathbf{E}[X]=\mathbf{E}\left[\sum_{i\lt j}X_{ij}\right]=\sum_{i\lt j}\mathbf{E}[X_{ij}]=\sum_{i\lt j}\Pr[X_{ij}=1]\le{n\choose 2}\frac{1}{M}\lt \frac{n^2}{2M}. }[/math]
In particular, for [math]\displaystyle{ n=M }[/math], i.e. [math]\displaystyle{ n }[/math] items are mapped to [math]\displaystyle{ n }[/math] hash values by a pairwise independent hash function, the expected collision number is [math]\displaystyle{ \mathbf{E}[X]\lt \frac{n^2}{2M}=\frac{n}{2} }[/math].
Birthday problem
In the context of hash functions, the birthday problem ask for the probability that there is no collision at all. Since collision is something that we want to avoid in the applications of hash functions, we would like to lower bound the probability of zero-collision, i.e. to upper bound the probability that there exists a collision pair.
The above analysis gives us an estimation on the expected number of collision pairs, such that [math]\displaystyle{ \mathbf{E}[X]\lt \frac{n^2}{2M} }[/math]. Apply the Markov's inequality, for [math]\displaystyle{ 0\lt \epsilon\lt 1 }[/math], we have
- [math]\displaystyle{ \Pr\left[X\ge \frac{n^2}{2\epsilon M}\right]\le\Pr\left[X\ge \frac{1}{\epsilon}\mathbf{E}[X]\right]\le\epsilon. }[/math]
When [math]\displaystyle{ n\le\sqrt{2\epsilon M} }[/math], the number of collision pairs is [math]\displaystyle{ X\ge1 }[/math] with probability at most [math]\displaystyle{ \epsilon }[/math], therefore with probability at least [math]\displaystyle{ 1-\epsilon }[/math], there is no collision at all. Therefore, we have the following theorem.
Theorem - If [math]\displaystyle{ h }[/math] is chosen uniformly from a 2-universal family of hash functions mapping the universe [math]\displaystyle{ [N] }[/math] to [math]\displaystyle{ [M] }[/math] where [math]\displaystyle{ N\ge M }[/math], then for any set [math]\displaystyle{ S\subset [N] }[/math] of [math]\displaystyle{ n }[/math] items, where [math]\displaystyle{ n\le\sqrt{2\epsilon M} }[/math], the probability that there exits a collision pair is
- [math]\displaystyle{ \Pr[\mbox{collision occurs}]\le\epsilon. }[/math]
- If [math]\displaystyle{ h }[/math] is chosen uniformly from a 2-universal family of hash functions mapping the universe [math]\displaystyle{ [N] }[/math] to [math]\displaystyle{ [M] }[/math] where [math]\displaystyle{ N\ge M }[/math], then for any set [math]\displaystyle{ S\subset [N] }[/math] of [math]\displaystyle{ n }[/math] items, where [math]\displaystyle{ n\le\sqrt{2\epsilon M} }[/math], the probability that there exits a collision pair is
Recall that for mutually independent choices of bins, for some [math]\displaystyle{ n=\sqrt{2M\ln(1/\epsilon)} }[/math], the probability that a collision occurs is about [math]\displaystyle{ \epsilon }[/math]. For constant [math]\displaystyle{ \epsilon }[/math], this gives an essentially same bound as the pairwise independent setting. Therefore, the behavior of pairwise independent hash function is essentially the same as the uniform random hash function for the birthday problem. This is easy to understand, because birthday problem is about the behavior of collisions, and the definition of 2-universal hash function can be interpreted as "functions that the probability of collision is as low as a uniform random function".
Perfect Hashing
Perfect hashing is a data structure for storing a static dictionary. In a static dictionary, a set [math]\displaystyle{ S }[/math] of [math]\displaystyle{ n }[/math] items from the universe [math]\displaystyle{ [N] }[/math] are preprocessed and stored in a table. Once the table is constructed, it will nit be changed any more, but will only be used for search operations: a search for an item gives the location of the item in the table or returns that the item is not in the table. You may think of an application that we store an encyclopedia in a DVD, so that searches are very efficient but there will be no updates to the data.
This problem can be solved by binary search on a sorted table or balanced search trees in [math]\displaystyle{ O(\log n) }[/math] time for a set [math]\displaystyle{ S }[/math] of [math]\displaystyle{ n }[/math] elements. We show how to solve this problem with [math]\displaystyle{ O(1) }[/math] time by perfect hashing.
Perfect hashing using quadratic space
The idea of perfect hashing is that we use a hash function [math]\displaystyle{ h }[/math] to map the [math]\displaystyle{ n }[/math] items to distinct entries of the table; store every item [math]\displaystyle{ x\in S }[/math] in the entry [math]\displaystyle{ h(x) }[/math]; and also store the hash function [math]\displaystyle{ h }[/math] in a fixed location in the table (usually the beginning of the table). The algorithm for searching for an item is as follows:
- search for [math]\displaystyle{ x }[/math] in table [math]\displaystyle{ T }[/math]:
- retrieve [math]\displaystyle{ h }[/math] from a fixed location in the table;
- if [math]\displaystyle{ x=T[h(x)] }[/math] return [math]\displaystyle{ h(x) }[/math]; else return NOT_FOUND;
This scheme works as long as that the hash function satisfies the following two conditions:
- The description of [math]\displaystyle{ h }[/math] is sufficiently short, so that [math]\displaystyle{ h }[/math] can be stored in one entry (or in constant many entries) of the table.
- [math]\displaystyle{ h }[/math] has no collisions on [math]\displaystyle{ S }[/math], i.e. there is no pair of items [math]\displaystyle{ x_1,x_2\in S }[/math] that are mapped to the same value by [math]\displaystyle{ h }[/math].
The first condition is easy to guarantee for 2-universal hash families. As shown by Carter-Wegman construction, a 2-universal hash function can be uniquely represented by two integers [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math], which can be stored in two entries (or just one, if the word length is sufficiently large) of the table.
Our discussion is now focused on the second condition. We find that it relies on the perfectness of the hash function for a data set [math]\displaystyle{ S }[/math].
A hash function [math]\displaystyle{ h }[/math] is perfect for a set [math]\displaystyle{ S }[/math] of items if [math]\displaystyle{ h }[/math] maps all items in [math]\displaystyle{ S }[/math] to different values, i.e. there is no collision.
We have shown by the birthday problem for 2-universal hashing that when [math]\displaystyle{ n }[/math] items are mapped to [math]\displaystyle{ n^2 }[/math] values, for an [math]\displaystyle{ h }[/math] chosen uniformly from a 2-universal family of hash functions, the probability that a collision occurs is at most 1/2. Thus
- [math]\displaystyle{ \Pr[h\mbox{ is perfect for }S]\ge\frac{1}{2} }[/math]
for a table of [math]\displaystyle{ n^2 }[/math] entries.
The construction of perfect hashing is straightforward then:
- For a set [math]\displaystyle{ S }[/math] of [math]\displaystyle{ n }[/math] elements:
- uniformly choose an [math]\displaystyle{ h }[/math] from a 2-universal family [math]\displaystyle{ \mathcal{H} }[/math]; (for Carter-Wegman's construction, it means uniformly choose two integer [math]\displaystyle{ 1\le a\le p-1 }[/math] and [math]\displaystyle{ b\in[p] }[/math] for a sufficiently large prime [math]\displaystyle{ p }[/math].)
- check whether [math]\displaystyle{ h }[/math] is perfect for [math]\displaystyle{ S }[/math];
- if [math]\displaystyle{ h }[/math] is NOT perfect for [math]\displaystyle{ S }[/math], start over again; otherwise, construct the table;
This is a Las Vegas randomized algorithm, which construct a perfect hashing for a fixed set [math]\displaystyle{ S }[/math] with expectedly at most two trials (due to geometric distribution). The resulting data structure is a [math]\displaystyle{ O(n^2) }[/math]-size static dictionary of [math]\displaystyle{ n }[/math] elements which answers every search in deterministic [math]\displaystyle{ O(1) }[/math] time.
FKS perfect hashing
In the last section we see how to use [math]\displaystyle{ O(n^2) }[/math] space and constant time for answering search in a set. Now we see how to do it with linear space and constant time. This solves the problem of searching asymptotically optimal for both time and space.
This was once seemingly impossible, until Yao's seminal paper:
- Yao. Should tables be sorted? Journal of the ACM (JACM), 1981.
Yao's paper shows a possibility of achieving linear space and constant time at the same time by exploiting the power of hashing, but assumes an unrealistically large universe.
Inspired by Yao's work, Fredman, Komlós, and Szemerédi discover the first linear-space and constant-time static dictionary in a realistic setting:
- Fredman, Komlós, and Szemerédi. Storing a sparse table with O(1) worst case access time. Journal of the ACM (JACM), 1984.
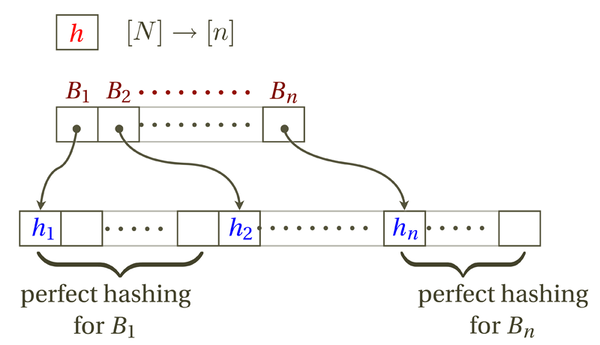
The idea of FKS hashing is to arrange hash table in two levels:
- In the first level, [math]\displaystyle{ n }[/math] items are hashed to [math]\displaystyle{ n }[/math] buckets by a 2-universal hash function [math]\displaystyle{ h }[/math].
- Let [math]\displaystyle{ B_i }[/math] be the set of items hashed to the [math]\displaystyle{ i }[/math]th bucket.
- In the second level, construct a [math]\displaystyle{ |B_i|^2 }[/math]-size perfect hashing for each bucket [math]\displaystyle{ B_i }[/math].
The data structure can be stored in a table. The first few entries are reserved to store the primary hash function [math]\displaystyle{ h }[/math]. To help the searching algorithm locate a bucket, we use the next [math]\displaystyle{ n }[/math] entries of the table as the "pointers" to the bucket: each entry stores the address of the first entry of the space to store a bucket. In the rest of table, the [math]\displaystyle{ n }[/math] buckets are stored in order, each using a [math]\displaystyle{ |B_i|^2 }[/math] space as required by perfect hashing.
It is easy to see that the search time is constant. To search for an item [math]\displaystyle{ x }[/math], the algorithm does the followings:
- Retrieve [math]\displaystyle{ h }[/math].
- Retrieve the address for bucket [math]\displaystyle{ h(x) }[/math].
- Search by perfect hashing within bucket [math]\displaystyle{ h(x) }[/math].
Each line takes constant time. So the worst-case search time is constant.
We then need to guarantee that the space is linear to [math]\displaystyle{ n }[/math]. At the first glance, this seems impossible because each instance of perfect hashing for a bucket costs a square-size of space. We will prove that although the individual buckets use square-sized spaces, the sum of the them is still linear.
For a fixed set [math]\displaystyle{ S }[/math] of [math]\displaystyle{ n }[/math] items, for a hash function [math]\displaystyle{ h }[/math] chosen uniformly from a 2-universe family which maps the items to [math]\displaystyle{ [n] }[/math], called [math]\displaystyle{ n }[/math] buckets, let [math]\displaystyle{ Y_i=|B_i| }[/math] be the number of items in [math]\displaystyle{ S }[/math] mapped to the [math]\displaystyle{ i }[/math]th bucket. We are going to bound the following quantity:
- [math]\displaystyle{ Y=\sum_{i=1}^n Y_i^2. }[/math]
Since each bucket [math]\displaystyle{ B_i }[/math] use a space of [math]\displaystyle{ Y_i^2 }[/math] for perfect hashing. [math]\displaystyle{ Y }[/math] gives the size of the space for storing the buckets.
We will show that [math]\displaystyle{ Y }[/math] is related to the total number of collision pairs. (Indeed, the number of collision pairs can be computed by a degree-2 polynomial, just like [math]\displaystyle{ Y }[/math].)
Note that a bucket of [math]\displaystyle{ Y_i }[/math] items contributes [math]\displaystyle{ {Y_i\choose 2} }[/math] collision pairs. Let [math]\displaystyle{ X }[/math] be the total number of collision pairs. [math]\displaystyle{ X }[/math] can be computed by summing over the collision pairs in every bucket:
- [math]\displaystyle{ X=\sum_{i=1}^n{Y_i\choose 2}=\sum_{i=1}^n\frac{Y_i(Y_i-1)}{2}=\frac{1}{2}\left(\sum_{i=1}^nY_i^2-\sum_{i=1}^nY_i\right)=\frac{1}{2}\left(\sum_{i=1}^nY_i^2-n\right). }[/math]
Therefore, the sum of squares of the sizes of buckets is related to collision number by:
- [math]\displaystyle{ \sum_{i=1}^nY_i^2=2X+n. }[/math]
By our analysis of the collision number, we know that for [math]\displaystyle{ n }[/math] items mapped to [math]\displaystyle{ n }[/math] buckets, the expected number of collision pairs is: [math]\displaystyle{ \mathbf{E}[X]\le \frac{n}{2} }[/math]. Thus,
- [math]\displaystyle{ \mathbf{E}\left[\sum_{i=1}^nY_i^2\right]=\mathbf{E}[2X+n]\le 2n. }[/math]
Due to Markov's inequality, [math]\displaystyle{ \sum_{i=1}^nY_i^2=O(n) }[/math] with a constant probability. For any set [math]\displaystyle{ S }[/math], we can find a suitable [math]\displaystyle{ h }[/math] after expected constant number of trials, and FKS can be constructed with guaranteed (instead of expected) linear-size which answers each search in constant time.